Determining the incidence of the hereditary form of retinoblastoma

Introduction

Lohmann and associates give comprehensive reviews of retinoblastoma (Rb) with pointers to additional sources (1,2). The American Cancer Society has an account of all aspects of the disorder (3). The National Eye Institute notes (4): “In some cases the disease is inherited from a parent”. Our objective is to give formulae for the gene frequency and incidence of this category of cases, so the emphasis is on population genetics.

Cases arise from germinal mutations which may or may not be transmitted to future generations in a dominant mode of inheritance. The model, known as the two-hit theory of carcinogenesis, is usually attributed to AG Knudson Jr (5,6). OMIM (7) states: “A number sign (#) is used with this entry [#180200] because hereditary Rb is caused by a heterozygous germline mutation on one allele and a somatic mutation on the other allele of the RB1 gene (614041) on chromosome 13q14”. OMIM gives four other references to Knudson as well as the two cited here.

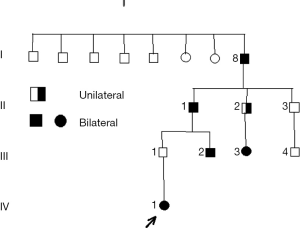
The pedigree in Figure 1 illustrates some of the characteristics of Rb, such as the possibility of transmission of a germinal mutation by an apparently unaffected parent (8). Individual I/8 was born in 1891; at the time of publication [1976], this man was still alive.

Figure 1 Pedigree of retinoblastoma [with permission from Migdal 1976 (8)].

Vogel [1979] gives a detailed review of Rb (9). He has some reservations about Knudson’s justification of his [Knudson’s] model, but ends with the statement: “However, one of Knudson’s conclusions can hardly be avoided: the manifestation of inherited R requires two independent events, one occurring in the germ cell and affecting the probability of a second, which occurs in precursor cells of retinal elements having a neuronal origin.”.

The object of this paper is to give formulae for the gene frequency of the Rb allele and the incidence of Rb as functions of the germinal mutation rate, the penetrance and the relative fitness of affected individuals.

Gene frequency and incidence of retinoblastoma (Rb)

Consider families in the segment of the population (sub-population) subject to the inherited form of Rb. Imagine that generations are discrete and non-overlapping. There are three genotypes: non-carriers, denoted by T₀, with frequency f₀; carriers, denoted by T₁, with frequency f₁; and bearers of two copies of the germinal mutation, denoted by T₂, with frequency f₂ (f₀ + f₁ + f₂ =1). The frequency of the Rb mutant is q = ½f₁ + f₂ and of the ‘normal’ allele is p = 1 − q.

Taking an arbitrary value of p near to 1 (and less than 1) and assuming random union of gametes, mutation of gametes produces frequency of type T₀:

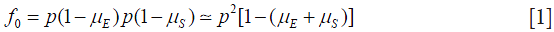
where is the rate of mutation to the Rb allele in eggs and 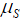is the rate in sperm. We show below that the results of interest depend on the sum 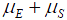rather than on the values separately, so replace the sum by that is take .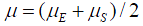

Because of selection against affected individuals, we assume that individuals of type T₂ will be so few in number that they can be neglected. Therefore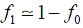

We assume that a proportion (1 − t) of carriers of the Rb allele do not have tumours, that are unaffected, and that, with probability s, those who do will not have children. Symbol t may be interpreted as the penetrance of the Rb allele. The frequency of carriers in the next generation is

and the frequency of the Rb allele is

Starting from an arbitrary value of p = 1 − q, applying Eqs. [1]-[3] for several generations leads to the following approximate values of q and the incidence of tumours r:

and

when t = 1, Eq. [5] reduces to

A formula similar to Eq. [6] has been in use for some time, although without consideration of the possibility that individuals of type T₁ may be unaffected. It occurs on page 177 in Carter [1977] in the following form (10)

Carter explains Eq. [7] in the following way: “The general relationship for conditions due to dominant genes between the proportion of children born affected which we will call A, the mutation rate, which we will call m, and the fitness of those affected, which we will call f, is given by the expression … (Eq. [7] above)”. The justification of Eq. [7] assumes an equilibrium between mutation which introduces copies of the Rb allele into the population and removal by reason of the relatively lower fitness of carriers – mutation at each of two chromosomes of a zygote at rate m per gamete is balanced by the removal of the fraction 1 − f of affected individuals each of whom has a single copy of the Rb allele.

Discussion

Westman describes Rb as a rare childhood cancer which occurs in 1 in 17,000 live births (11). This is approximately 60 per million. She states that 60% are sporadic and the remaining 40%, that is 24 per million, are caused by inherited mutation. Russell estimates that the mutation rate is between 5 and 12 per million gametes (12). If we take µ as 8 per million, s=0.4, and t=0.95, Eq. [5] gives incidence about 25 per million births. Figure 2 gives some idea of the effect of variations in the values of s and t, for this rate of mutation.

Figure 2 Incidence (per million births) of hereditary retinoblastoma, if the germinal mutation rate µ=8 per million gametes, for two levels of penetrance t and a range of selection coefficients s.

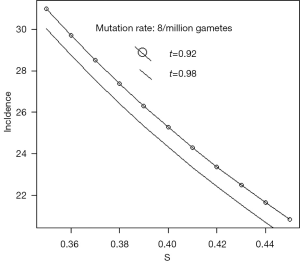
Figure 1 of Moll et al. shows that the survival of hereditary cases was about 70% at age 40 (13). Kivelä [1999] reports that hereditary cases comprised 47% of all cases in the sample reviewed (14).

Kivelä [2009] emphasizes the difficulty of estimating the true incidence of Rb and the mortality rates (15).

Gündüz et al. summarize recent experience in Ankara, Turkey in treatment of cases of Rb (16).

The formulae can give only some approximations which may be useful in considering the effects of public health measures. A major debatable assumption is that the population is near to equilibrium between mutation and the selective process. Advances in medical science and practice lead to changes in survival and ultimately to changes in q and r. The absence of tumour does not necessarily imply no loss of fitness since Westman notes that individuals with familial Rb have an increased risk of osteosarcomas or fibrosarcomas and melanomas in later life.

Russell notes (12):

Mutations in a gene called RB are responsible for Rb. In patients with hereditary Rb, the tumor cells always have mutations in both RB genes, while in all normal cells from the same individuals, one of the two RB genes has the mutation. Thus, a second mutation is all that is needed in the normal cells to change to a tumor cell. Using the molecularly cloned RB gene for molecular analysis of hereditary Rb patients, researchers have found that, in a significant fraction of cases, the second mutation produces a mutated allele that is identical to the inherited mutated allele. This means that the normal wild-type copy of the Rb gene is somehow replaced by a duplicated copy of the homologous chromosome region carrying the mutated allele. While there are several mechanisms that could account for this phenomenon, one possibility is that mitotic recombination is the cause.

Russell gives a detailed description of the mechanism of hereditary Rb and compares it with what he calls sporadic Rb. His textbook is just a brief entrée to a large and complex literature on the subject.

Acknowledgements

None.

Footnote

Conflicts of Interest: The author has no conflict of interest to declare.

References

1. Lohmann D, Gallie B, Dommering C, et al. Clinical utility gene card for: retinoblastoma. Eur J Hum Genet 2011.19. [PubMed]
2. Lohmann DR, Gallie BL. Retinoblastoma. GeneReviews® [Internet]: Initial Posting: July 18, 2000; Last update: November 19, 2015; Available online: http://www.ncbi.nlm.nih.gov/books/NBK1452.
3. American Cancer Society. Available online: http://www.cancer.org/search/index?QueryText=retinoblastoma&Page=1
4. National Eye Institute. Available online: https://nei.nih.gov/health/retinoblastoma
5. Knudson AG Jr. Mutation and cancer: statistical study of retinoblastoma. Proc Natl Acad Sci U S A 1971;68:820-3. [Crossref] [PubMed]
6. Hethcote HW, Knudson AG Jr. Model for the incidence of embryonal cancers: application to retinoblastoma. Proc Natl Acad Sci U S A 1978;75:2453-7. [Crossref] [PubMed]
7. OMIM. Available online: http://www.omim.org/entry/180200?search=retinoblastoma&highlight=retinoblastoma
8. Migdal C. Retinoblastoma occurring in four successive generations. Br J Ophthalmol 1976;60:151-2. [Crossref] [PubMed]
9. Vogel F. Genetics of retinoblastoma. Hum Genet 1979;52:1-54. [Crossref] [PubMed]
10. Carter CO. Human Heredity (Second edition). Harmondsworth, Middlesex, England: Penguin Books Ltd, 1977.
11. Westman JA. Medical Genetics for the Modern Clinician. Philadelphia: Lippincott Williams & Wilkins, 2006.
12. Russell PJ. iGenetics: A Molecular Approach (Second edition). San Francisco: Benjamin Cummings, 2006.
13. Moll AC, Imhof SM, Bouter LM, et al. Second primary tumors in patients with hereditary retinoblastoma: a register-based follow-up study, 1945-1994. Int J Cancer 1996;67:515-9. [Crossref] [PubMed]
14. Kivelä T. Trilateral retinoblastoma: a meta-analysis of hereditary retinoblastoma associated with primary ectopic intracranial retinoblastoma. J Clin Oncol 1999;17:1829-37. [PubMed]
15. Kivelä T. The epidemiological challenge of the most frequent eye cancer: retinoblastoma, an issue of birth and death. Br J Ophthalmol 2009;93:1129-31. [Crossref] [PubMed]
16. Gündüz K, Köse K, Kurt RA, et al. Retinoblastoma in Turkey: results from a tertiary care center in Ankara. J Pediatr Ophthalmol Strabismus 2013;50:296-303. [Crossref] [PubMed]