
Development and evaluation of a radiomics model of resting 13N-ammonia positron emission tomography myocardial perfusion imaging to predict coronary artery stenosis in patients with suspected coronary heart disease
Introduction
Coronary heart disease (CHD) is characterized by myocardial ischemia, hypoxia, and necrosis due to coronary artery stenosis or occlusion, and is often accompanied by symptoms of chest distress and chest pain, posing a serious hazard to human health (1-3). Severe coronary stenosis often requires revascularization (4,5). Comprehensive preoperative examination is of great importance for correct decision-making and improving the curative effect and prognosis.
Coronary stenosis is often evaluated using coronary angiography (CAG) or coronary computed tomography (CT) angiography, of which CAG is the gold standard (6-8). Both methods use iodine contrast agents, which can cause allergic reactions or kidney damage (9,10). In addition, CAG is expensive, complex, and invasive and may lead to various complications (11).
Myocardial positron emission tomography (PET) imaging can be used to qualitatively or quantitatively evaluate pathological changes in the myocardium in CHD patients (12). For example, resting 13N-ammonia (13N-NH3) PET myocardial perfusion imaging (MPI) is commonly used, and it can be combined with stress MPI and used in the diagnosis of myocardial ischemia and infarction. It can also be combined with 18F-FDG PET myocardial metabolic imaging (MMI) and used for the assessment of myocardial vitality (13).
A study has reported that stress MPI can be used to predict coronary artery stenosis (14). A study in our center also confirmed that resting MPI-MMI parametric results can be used to predict coronary stenosis (15). However, stress MPI has certain risks, and the preparation process of MMI is complicated. Additionally, it may be affected by diabetes, blood glucose level, and other factors. Moreover, the image quality is not ideal in some cases (16). Therefore, it is necessary to develop a safe, noninvasive, and accurate method for predicting coronary stenosis.
Severe coronary stenosis results in reduced myocardial blood flow (MBF) and microstructural damage (13,17-19). This change affects grayscale patterns and pixel interrelationships in the image, which may not be detected by the naked eye. Currently, it can be quantitatively evaluated using radiomics (20,21). In recent years, several studies have evaluated the application value of myocardial radiomics in CHD, but there are few studies on the prediction of coronary artery stenosis using myocardial radiomics (22-24).
Radiomics features usually have a large amount of data, and it is difficult to obtain ideal results by traditional methods. However, machine learning algorithms can improve the prediction performance and outperform the traditional one-dimensional statistical methods by specifically finding associations between data. Therefore, we extracted the radiomics features of 3 coronary segments of the left ventricular (LV) myocardium on resting MPI and constructed a model using the machine learning method to predict coronary stenosis. The radiomics model was comprehensively evaluated through comparison with the conventional parameter model and through subgroup analysis. We present the following article in accordance with the TRIPOD reporting checklist (available at https://atm.amegroups.com/article/view/10.21037/atm-22-4692/rc).
Methods
Owing to the particularity of cardiac research, in this work, we followed the recommendations of the European Association of Cardiovascular Imaging and the European Association of Nuclear Medicine to standardize the application of artificial intelligence in multimodal cardiovascular imaging (25).
Patients
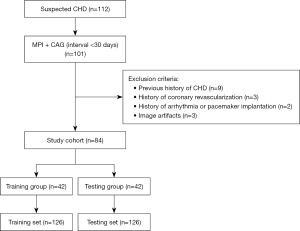
This retrospective diagnostic study included patients who underwent resting 13N-NH3 PET MPI and CAG at Guangdong Provincial People’s Hospital from November 2016 to December 2021 due to suspected CHD.
The inclusion criteria were as follows: (I) adult patients; (II) suspected CHD due to chest tightness, chest pain, and abnormal electrocardiogram (ECG); (III) resting MPI and CAG performed successively with an interval of no more than 30 days; and (IV) complete clinical and imaging data.
The exclusion criteria were as follows: (I) previous history of CHD; (II) history of coronary revascularization; (III) history of arrhythmia or pacemaker implantation; and (IV) inability to evaluate the original image due to dislocation artifacts caused by poor breath-holding, body movement, and other reasons.
The patient selection process is illustrated in Figure 1. The demographic and clinical information of the selected patients were recorded. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). This study was approved by the ethics committee of the Guangdong Provincial People’s Hospital (No. KY-Q-2022-345-01), and individual patient consent for this retrospective analysis was waived.
PET/CT acquisition and data analysis
The resting MPI scans were performed in 3D list-mode on a Siemens Biograph 16 PET/CT scanner. In the resting state, the patient was intravenously injected with 15–25 mCi (555–925 Mbq) 13N-NH3 on the scanner, and continuous perfusion acquisition for 15 min was immediately initiated. ECGs were collected during the cardiac-gated triggering scan. The patients were instructed to breathe normally and to avoid deep breathing, speaking, and body movements to prevent image dislocation.
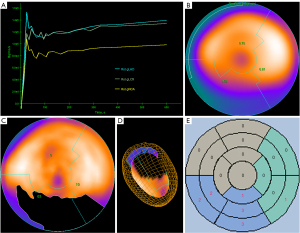
Data were reconstructed by an ordered subset expectation maximization algorithm with 2 iterations per 24 subsets, a matrix size of 168×168, a voxel size of 4.1×4.1×2.0 mm, and a gaussian filter at 5.0 mm full-width at half-maximum. MPI data were reconstructed into static and dynamic images, and the dynamic images were reconstructed into 21 frames (12×10, 6×30, 2×60, and 1×180 seconds). A doctor (Doctor 1) with 10 years of experience who was blinded to original MPI measurements determined the LV contour and generated a polar map using the commercially available QPS/QGS software (Cedars-Sinai Medical Center, Los Angeles, CA, USA). Manual corrections of LV position, angle orientation, and valve plane position were performed when necessary. The LV image was divided into 3 coronary segments [left anterior descending coronary artery (LAD), left circumflex coronary artery (LCX), and right coronary artery (RCA)] on a polar map according to the American Heart Association criteria. The conventional parameters of each segment were obtained: MBF, perfusion defect extent (EXT), total perfusion deficit (TPD), and summed rest score (SRS) (Figure 2). MBF was obtained from dynamic imaging data and represented absolute blood flow quantification through a unit mass of myocardium per unit time (mL/min/g). The EXT, TPD, and SRS were obtained from static images. EXT represents the percentage of the perfusion defect extent, TPD comprehensively reflects the percentage of the extent and severity of perfusion defects, and SRS is a semi-quantitative parameter used to evaluate the severity of perfusion defects. This was the sum of the tracer uptake scores in each segment (0: normal, 1: slight reduction, 2: moderate reduction, 3: severe reduction, 4: no distribution).
CAG
All the patients underwent CAG within 30 days of the myocardial PET scan. A doctor (Doctor 2) reviewed the CAG report and determined the degree of stenosis of the left main coronary artery (LM) and the 3 coronary arteries. LM lumen stenosis >50%, LAD, LCX, and RCA lumen stenosis >75% were considered to be significant stenosis and were used as the standard for obstructive CHD.
Segmentation and radiomics feature extraction
The myocardium of the LV coronary segments was segmented using a semi-automatic segmentation algorithm based on the Carimas version 2.10 software (Turku PET Center, Finland) by Doctor 1 who was blinded to patient characteristics and CAG results. First, the DICOM image of the static image was loaded. Second, 3 locations of the heart (the apex of the LV, base of the LV, and RV) were repositioned. Third, the software automatically searched ventricular boundaries to obtain the initial 3D-volume of interest (VOI) and generate a MASK, which could be manually adjusted to improve quality. Finally, LAD, LCX, and RCA segment masks were delineated based on the LV MASK for feature extraction (Figure 3).
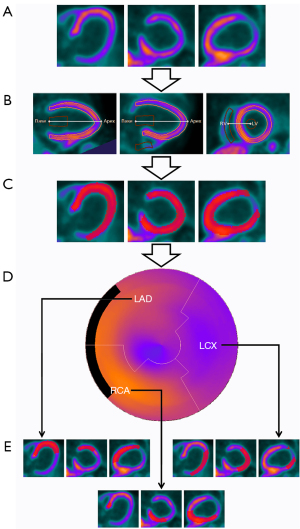
Radiomics features were extracted using the PyRadiomics package on Feature Explorer Pro (FAE version 0.4.4), an open-source machine learning platform based on Python. Three feature categories were extracted: (I) first-order (statistics) features; (II) shape-based features; and (III) texture features [including gray-level co-occurrence matrix (GLCM), gray-level run-length matrix (GLRLM), gray-level size zone matrix (GLSZM), gray-level dependence matrix (GLDM), and neighborhood gray-level difference matrix (NGTDM)]. In addition, 9 filters [including wavelet transform, square, square root, Laplacian of Gaussian, logarithm, exponential, gradient, local binary pattern (2D), and local binary pattern (3D)] were applied to the original images to obtain derived images. Except for the shape-based images, all the other features were calculated for the original and derived images.
Reproducibility of radiomics features
Thirty patients were randomly selected, and image segmentation of 90 coronary segments was performed again by 2 nuclear medicine doctors (Doctor 1 with 10 years of experience and Doctor 3 with 20 years of experience). Intraclass correlation coefficients (ICCs) for each radiomics feature were calculated after segmentation to assess inter-observer repeatability.
Modeling
All patients were randomly divided into the training and testing groups at a 1:1 ratio, and their coronary segments were used as the training and testing sets, respectively. The training set was used for feature and parameter selection and model development, while the testing set was used for model evaluation and subgroup analysis. In the training set, FAE software was used to implement the machine learning algorithm according to the process of “balance data” - “normalization” - “preprocess” - “feature selection” - “classifier”, and the conventional parameter (MPI model) and radiomics (Rad model) models for predicting significant coronary stenosis (>75%) were established. The synthetic minority oversampling technique was used to balance positive and negative samples. Z-scores were used for normalization. If the Pearson correlation coefficient value of the feature pair was larger than 0.9, one of them was randomly removed. The maximum number of features was 20, the feature selection method was recursive feature extraction (RFE), and the classifier was a support vector machine (SVM). A 5-fold cross-validation was applied to the training set for model evaluation. The model with the largest area under the curve (AUC) in the cross-validation set was selected as the best model and tested in the testing set. After the best MPI and Rad models were selected, the MPI and Rad scores of each segment were calculated. The 2 models were combined to establish a nomogram, and the risk score for each segment was calculated. The discriminant ability of the models was evaluated using the AUC, accuracy, sensitivity, and specificity. The net clinical benefit of the models was assessed using decision curve analysis (DCA). The agreement between the observed and predicted values of the model was demonstrated by the calibration curves.
Subgroup analysis
To evaluate whether the selected models had good and stable performance under different conditions, we conducted multiple subgroup analyses in the testing set including the following: (I) different myocardial segments (LAD, LCX, RCA); (II) number of stenotic vessels (0–1, 2–3 coronary stenoses); (III) presence of LM stenosis; (IV) different cardiac risk factors (hypertension, diabetes); (V) the total injection dose of 13N-NH3 (15–20, 20–25 mCi); and (VI) the unit injection dose of 13N-NH3 (0.20–0.30, 0.30–0.50 mCi/kg). The performance of the models was evaluated using the AUC.
Statistical analysis
Classification variables are presented as frequency (percentage), and normally distributed continuous variables are presented as mean ± standard deviation. Continuous variables with a non-normal distribution are presented as median (interquartile range). The independent-sample t-test, χ2 test, or Mann-Whitney U test were used to evaluate the differences between sets. The differences between AUCs were assessed using the DeLong test. The matching degree of the calibration curves was evaluated by the unreliability test. Statistical significance was set at P<0.05, and bilateral tests were used. SPSS (version 20.0; IBM Corporation, Armonk, NY, USA) was used for all statistical analyses. R (version 4.0.3, R Foundation for Statistical Computing, Vienna, Austria) with RStudio (version 1.4.1717) was used to draw parts of the figures.
Results
Patients and coronary segments
This study included 84 patients (42 in the training group and 42 in the testing group). The average age was 57.3±10.1 years old, and 91.7% of the patients were male. CAG confirmed that 75 (89.3%) patients had CHD and 9 (10.7%) did not. Among them, 15 (17.9%), 34 (40.5%), and 26 (31.0%) patients had 1-, 2-, and 3-vessel stenosis, respectively, and 22 (26.2%) had LM stenosis. The baseline characteristics and CAG results of patients are shown in Table 1. The results showed no significant difference between the training and testing groups (P>0.05). There were 252 coronary segments in 84 patients (both the training and testing sets included 126 coronary segments). CAG showed 161 coronary artery stenoses (63.9%) and 61 (72.6%), 38 (45.2%), and 62 (73.8%) stenoses of the LAD, LCX, and RCA, respectively. Quantitative analysis of resting MPI showed that the medians (interquartile ranges) of MBF, EXT, TPD and SRS of all segments were 0.61 mL/g/min (0.47–0.76 mL/g/min), 22% (8–49%), 20% (7–45%), and 6 [2–10], respectively. The CAG and resting MPI results of the segments are shown in Table 2. No significant differences were observed between the 2 sets (P>0.05).
Table 1
| Variables | Training group, n=42 | Testing group, n=42 | P value |
|---|---|---|---|
| Demographic | |||
| Gender | |||
| Male | 37 (88.1) | 40 (95.2) | 0.430 |
| Female | 5 (11.9) | 2 (4.8) | |
| Age (years) | 56.2±9.8 | 58.4±10.5 | 0.335 |
| Body mass index (kg/m2) | 23.3±2.6 | 24.0±3.2 | 0.268 |
| Cardiac risk factors | |||
| Smoking | |||
| Yes | 19 (45.2) | 20 (47.6) | 0.827 |
| No | 23 (54.8) | 22 (52.4) | |
| Alcoholism | |||
| Yes | 3 (7.1) | 4 (9.5) | 1.000 |
| No | 39 (92.9) | 38 (90.5) | |
| Diabetes mellitus | |||
| Yes | 17 (40.5) | 15 (35.7) | 0.653 |
| No | 25 (59.5) | 27 (64.3) | |
| Hypertension | |||
| Yes | 17 (40.5) | 16 (38.1) | 0.823 |
| No | 25 (59.5) | 26 (61.9) | |
| Dyslipidemia | |||
| Yes | 6 (14.3) | 4 (9.5) | 0.736 |
| No | 36 (85.7) | 38 (90.5) | |
| Family history of CHD | |||
| Yes | 2 (4.8) | 2 (4.8) | 1.000 |
| No | 40 (95.2) | 40 (95.2) | |
| Number of stenotic vessels | |||
| 0–1 vessel | 13 (31.0) | 11 (26.2) | 0.629 |
| 2–3 vessels | 29 (69.0) | 31 (73.8) | |
| Left main trunk stenosis | |||
| Yes | 10 (23.8) | 12 (28.6) | 0.620 |
| No | 32 (76.2) | 30 (71.4) | |
| Dose of 13N-NH3 | |||
| Total dose (mCi) | 19.7±2.8 | 20.8±3.4 | 0.101 |
| 15–20 | 21 (50.0) | 18 (42.9) | 0.512 |
| 20–25 | 21 (50.0) | 24 (57.1) | |
| Unit dose (mCi/kg) | 0.32±0.073 | 0.32±0.081 | 0.801 |
| 0.20–0.30 | 18 (42.9) | 19 (45.2) | 0.826 |
| 0.30–0.50 | 24 (57.1) | 23 (54.8) |
Classification variables are presented as n (%), and normally distributed continuous variables are presented as mean ± SD. CHD, coronary heart disease.
Table 2
| MPI parameters and CAG results | Training set | Testing set | P value |
|---|---|---|---|
| Number of segments, n | 126 | 126 | |
| MBF (mL/g/min) | 0.57 [0.46–0.76] | 0.65 [0.48–0.79] | 0.336 |
| EXT (%) | 21 [9–50] | 25 [8–48] | 0.989 |
| TPD (%) | 20 [8–46] | 21 [6–44] | 0.977 |
| SRS | 6 [2–10] | 6 [2–10] | 0.877 |
| Number of LAD/LCX/RCA, n | 42/42/42 | 42/42/42 | |
| Vascular stenosis of 3 vessels | |||
| Yes | 79 (62.7) | 82 (65.1) | 0.694 |
| No | 47 (37.3) | 44 (34.9) | |
| Vascular stenosis of LAD | |||
| Yes | 31 (73.8) | 30 (71.4) | 0.807 |
| No | 11 (26.2) | 12 (28.6) | |
| Vascular stenosis of LCX | |||
| Yes | 18 (42.9) | 20 (47.6) | 0.661 |
| No | 24 (57.1) | 22 (52.4) | |
| Vascular stenosis of RCA | |||
| Yes | 30 (71.4) | 32 (76.2) | 0.620 |
| No | 12 (28.6) | 10 (23.8) |
Continuous variables with a non-normal distribution are presented as median [interquartile range], and classification variables are presented as n (%). MPI, myocardial perfusion imaging; CAG, coronary angiography; MBF, myocardial blood flow; EXT, defect extent; TPD, total perfusion deficit; SRS, summed rest score; LAD, left anterior descending coronary artery; LCX, left circumflex coronary artery; RCA, right coronary artery.
Modeling
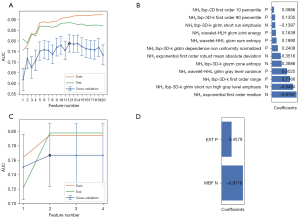
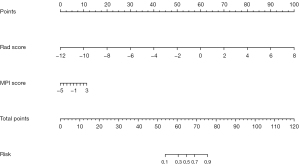
We extracted 1,781 radiomics features from the original and derived images of the resting MPI. After excluding features with a variance close to 0, 1,206 features were obtained. After removing features with an ICC <0.9, 996 features remained. After “balance data”, “normalization”, and “preprocess” (Pearson correlation analysis), 211 features remained (Figure 4). Through the SVM-RFE machine learning process of 5-fold cross-validation, 20 radiomics models were generated, and the model with the largest AUC (0.788) in the cross-validation set was selected as the Rad model (Figure 5A). The Rad model was composed of 12 radiomics features. The selected features and their corresponding coefficients are shown in Figure 5B. The radiomics score of each segment, calculated using the Rad model, is shown in Figure S1. After approximately the same modeling process, the obtained MPI model was composed of 2 parameters: MBF and EXT. The model selection process and parameter coefficients are shown in Figure 5C,5D. The Rad model was combined with the MPI model to establish a combined model in the form of a nomogram (Figure 6).
Machine learning model performance
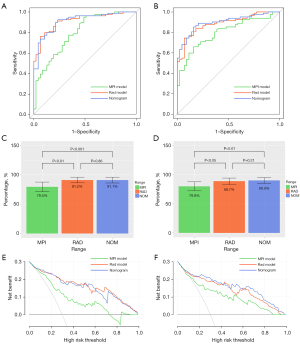
The AUC, accuracy, sensitivity, and specificity of the MPI model were, respectively, 0.795, 0.778, 0.937, and 0.511 in the training set and 0.798, 0.722, 0.659, and 0.841 in the testing set. The AUC, accuracy, sensitivity, and specificity of the Rad model were, respectively, 0.912, 0.825, 0.760, and 0.936 in the training set and 0.887, 0.810, 0.744, and 0.932 in the testing set. The AUC, accuracy, sensitivity, and specificity of the nomogram were, respectively, 0.911, 0.865, 0.924, and 0.766, in the training set and 0.900, 0.849, 0.854, and 0.841 in the testing set. The results are shown in Table 3 and Figure 7A,7B. The DeLong test showed that the AUCs of the Rad model and nomogram were significantly higher than that of the MPI model, but there was no significant difference between the AUC of the Rad model and nomogram (Figure 7C,7D). The DCA showed that the net clinical benefit of the Rad model and nomogram was similar but greater than that of the MPI model (Figure 7E,7F). The calibration curve showed good agreement between the observed and predicted values of the Rad model, and the P values of the unreliability test in the 2 sets were greater than 0.05 (Figure S2). Based on these results, we conducted a subgroup analysis of the Rad model.
Table 3
| Models | AUC (95% CI) | Cut off | Accuracy | Sensitivity | Specificity |
|---|---|---|---|---|---|
| Training group | |||||
| MPI model | 0.795 (0.713–0.876) | −0.777 | 0.778 | 0.937 | 0.511 |
| Rad model | 0.912 (0.862–0.962) | 0.808 | 0.825 | 0.760 | 0.936 |
| Nomogram | 0.911 (0.860–0.962) | 0.455 | 0.865 | 0.924 | 0.766 |
| Testing group | |||||
| MPI model | 0.798 (0.721–0.875) | 0.158 | 0.722 | 0.659 | 0.841 |
| Rad model | 0.887 (0.830–0.943) | 0.705 | 0.810 | 0.744 | 0.932 |
| Nomogram | 0.900 (0.847–0.953) | 0.641 | 0.849 | 0.854 | 0.841 |
AUC, area under the curve; CI, confidence interval; MPI, myocardial perfusion imaging; Rad, radiomics.
Subgroup analysis
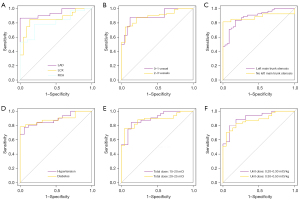
Subgroup analysis in the testing set showed that the ability of the Rad model to distinguish coronary stenosis (ROC AUC) was not significantly different (DeLong test) among subgroups divided by myocardial segments, number of stenotic vessels, LM stenosis, CHD risk factors, and total and unit injection dose of 13N-NH3. The AUCs between the LAD and RCA subgroups showed the largest difference (0.939 vs. 0.806), but there was no statistical difference between them (P=0.096) (Table 4, Figure 8).
Table 4
| Subgroups | Number of patients | Number of segments | AUC (95% CI) | Accuracy | Sensitivity | Specificity | P value |
|---|---|---|---|---|---|---|---|
| Myocardial segment | |||||||
| LAD | 42 | 42 | 0.939 (0.871–1.000) | 0.905 | 0.867 | 1.000 | 0.258a |
| LCX | 42 | 42 | 0.857 (0.733–0.980) | 0.857 | 0.850 | 0.864 | 0.096b |
| RCA | 42 | 42 | 0.806 (0.669–0.944) | 0.786 | 0.781 | 0.800 | 0.594c |
| Number of stenotic vessels | |||||||
| 0–1 | 11 | 33 | 0.895 (0.745–1.000) | 0.879 | 0.875 | 0.880 | 0.931 |
| 2–3 | 31 | 93 | 0.888 (0.817–0.958) | 0.785 | 0.743 | 0.947 | |
| Left main trunk stenosis | |||||||
| No | 30 | 90 | 0.885 (0.817–0.953) | 0.833 | 0.836 | 0.829 | 0.999 |
| Yes | 12 | 36 | 0.885 (0.772–0.997) | 0.861 | 0.815 | 1.000 | |
| Cardiac risk factors | |||||||
| Hypertension | 16 | 48 | 0.886 (0.795–0.978) | 0.833 | 0.774 | 0.941 | 0.932 |
| Diabetes | 15 | 45 | 0.892 (0.799–0.985) | 0.844 | 0.781 | 1.000 | |
| Total dose of 13N-NH3 | |||||||
| 15–20 mCi | 18 | 54 | 0.895 (0.812–0.978) | 0.852 | 0.844 | 0.864 | 0.823 |
| 20–25 mCi | 24 | 72 | 0.882 (0.803–0.960) | 0.819 | 0.760 | 0.955 | |
| Unit dose of 13N-NH3 | |||||||
| 0.20–0.30 mCi/kg | 19 | 57 | 0.909 (0.834–0.984) | 0.842 | 0.800 | 0.909 | 0.570 |
| 0.30–0.50 mCi/kg | 23 | 69 | 0.877 (0.797–0.957) | 0.783 | 0.702 | 0.955 | |
The P value represents the result of the DeLong test of AUCs between subgroups. a, P value between the LAD and LCX subgroup; b, P value between the LAD and RCA subgroup; c, P value between the LCX and RCA subgroup. Rad, radiomics; AUC, area under the curve; CI, confidence interval; LAD, left anterior descending coronary artery; LCX, left circumflex coronary artery; RCA, right coronary artery.
Discussion
In patients with CHD, resting MPI is rarely used alone. It is usually combined with stress MPI or MMI for the evaluation of ischemia, infarction, hibernation, and myocardial scarring, thus providing a basis for subsequent treatment decisions (13). If the resting MPI data can be used to accurately predict coronary stenosis and reduce the risk of injury caused by CAG, this will be of great significance.
Radiomics has been widely used in medical research as a novel, inexpensive, and noninvasive quantitative imaging technique (26,27). However, PET radiomics studies are mainly focused on 18F-FDG imaging of tumors, while there are few radiomics studies on cardiac PET imaging, let alone 13N-NH3 (25). Although there are many studies on cardiac MRI radiomics, most of them evaluated myocardial ischemia, infarction, or fibrosis, while there are none on the prediction of coronary stenosis (28). To our knowledge, this is the first study to predict coronary stenosis using 13N-NH3 PET radiomics.
13N-NH3 is a fat-soluble substance that can pass freely through the cell membrane. 13N-NH3 enters and remains in cardiomyocytes via the cell membrane through passive diffusion (29). Myocardial uptake of 13N-NH3 was positively correlated with MBF. When coronary artery stenosis is severe, MBF is reduced and the myocardial microstructure is destroyed (13,17-19). Both factors change the distribution of 13N-NH3 in myocardial tissue and then change the radiomics features of MPI. Therefore, we attempted to establish a statistical association between radiomics features and coronary stenosis using machine learning methods. The Rad model is composed of first-order and texture features without shape-based features. The first-order features mainly reflect changes in MBF, and the texture features mainly reflect changes in the myocardial microstructure. We believe that the Rad model reveals an association between the 2 categories of features and coronary stenosis.
Image segmentation has always been the focus and difficulty of radiomics (30). In the study of cardiac magnetic resonance radiomics, the combination of automatic contour drawing and limited manual correction is advocated, which has high efficiency and repeatability (20). Our segmentation task consisted of LV segmentation and coronary segment segmentation, which were completed using Carimas software. In LV segmentation, the MASK file of LV VOI could be obtained through the semi-automatic segmentation algorithm of the software and manual adjustment (31,32). In coronary segment segmentation, the VOI-MASK was further divided into MASK files of 3 coronary segments (LAD-MASK, LCX-MASK, and RCA-MASK) according to the American Heart Association standards. The advantages of this segmentation method are as follows: (I) the operation is convenient and fast, as it takes only 2–3 min to complete the segmentation of 3 coronary segments in a patient; (II) the obtained radiomics information is complete and rich because MASK files cover 3D and continuous layers of coronary segments, which is different from those studies that only analyze the maximum section or even polar map (33,34); (III) the repeatability is good, and >80% (996/1,206) radiomics features show high inter-observer repeatability (ICC ≥0.9).
With the advent of the era of precision medicine, various types of “big data” have been applied in clinical research (35,36). For complex available data, algorithms can be specifically used to find correlations between data, improve the predictive power of the model, and provide clinically relevant and useful results (37). Therefore, machine learning is increasingly used in the cardiovascular field (38). The FAE software is a Python-based radiomics and machine learning modelling tool developed by Song et al. It integrates the processes of feature extraction, data cleaning, binary classification modelling, result analysis, and visualization (39). The FAE software provides 4 classifiers and 10 feature selection methods, with a total of 40 combinations. To simplify the research process, only SVM-RFE was selected. SVM-RFE is a backward recursive elimination feature-selection algorithm that applies an SVM to high-dimensional data. It was first proposed by Guyon et al. for gene selection and achieved very good results (40). After continuous improvements, its performance and efficiency continued to increase. Currently, it is also applied to proteomics, radiomics, and other fields to improve the prediction accuracy of models (41-44). In our study, SVM-RFE was used to screen out 12 radiomics features to construct the Rad model, as well as 2 MPI parameters to construct the MPI model. These 2 models were then combined to construct a nomogram.
The 3 models calculated the risk score of each segment and predicted high-risk coronary arteries. In a study conducted at our center, MPI and MMI conventional parameters were combined to predict coronary stenosis using the machine learning method (15). The AUC of the best model was 0.856, which was better than that of the MPI model (AUC: 0.795) but inferior to the Rad model (AUC: 0.912) and nomogram (AUC: 0.911). In general, the nomogram showed better performance than the Rad model; however, there was no significant difference in the AUCs between them. This was because in the nomogram, the relative weights of the Rad model were far greater than those of the MPI model, and the nomogram was weighted heavily towards the Rad model, which produced better performance. Specifically, the radiomics features of the Rad model could have covered or even replaced the conventional parameters of the MPI model. Whether it indicates that radiomics features can predict conventional MPI parameters needs to be tested in future studies. The DCA for evaluating the net clinical benefit yielded similar results. Therefore, we chose the Rad model for subgroup analysis.
To ensure a sufficient sample size in each subgroup in the subgroup analysis, we divided the training and testing sets in a 1:1 ratio. As no relevant study has been conducted before, it was unclear which factors would affect the performance of the Rad model. Based on our experience, we selected specific factors for the subgroup analysis. First were the different myocardial segments (LAD, LCX, and RCA). Second was the injection dose of 13N-NH3, including total and unit doses. 13N-NH3 has a short half-life of approximately 10 min, making fixed-unit dose injection difficult to achieve (29). Therefore, in clinical practice, the total dose is often controlled between 10–30 mCi (13). The total dose in our study was within this range; however, the unit dose varied widely from 0.20 to 0.50 mCi/kg. We divided them into 2 subgroups (0.20–0.30 and 0.30–0.50 mCi/kg) for analysis and comparison. Third were the factors affecting hemodynamic status, including LM stenosis and the number of stenotic coronary arteries (45-47). For the former, we divided LM into stenosis and non-stenosis subgroups with >50% as the threshold, and the latter was divided into 2 subgroups: 0–1 vessel stenoses and 2–3 vessels stenoses. Fourth were the factors that may lead to microcirculatory lesions, including hypertension and diabetes (48-50), which were analyzed in separate subgroups. The final result showed that the AUC difference between the LAD and RCA subgroups was the largest (0.939 vs. 0.806), but there was no statistical difference between them (P=0.096). There was no statistical difference between the other subgroups (Figure 8, Table 4). This shows that the Rad model is not affected by subgroup factors and has good generalization ability.
This study has some limitations. First, this was a single-center, small-sample, retrospective study without external validation, and sampling error may affect the statistical results. Second, only patients with suspected CHD were included, excluding confirmed cases with a history of CHD. We speculated that the treatment process (drugs or surgery) of CHD might change myocardial radiomics characteristics and affect the prediction efficiency of the model. Therefore, only suspected untreated patients were included in the study. However, this might lead to selection bias and render the prediction model unsuitable for the general population. Third, stress MPI was excluded in this study. The Rad model was not compared with stress MPI, Rad model + stress MPI, or even stress MPI radiomics models. Therefore, in future research, efforts should be made in several aspects: obtaining a prospective, external independent validation cohort; extending the model to general patients with CHD; and incorporating stress MPI into the evaluation system.
Conclusions
In patients with suspected CHD, the radiomics machine learning model based on resting MPI can accurately predict coronary stenosis, which is better than the resting MPI conventional parameter model. In clinical practice, this noninvasive tool can help improve risk stratification. In the subgroup analysis, the Rad model was not affected by grouping factors and had good generalization ability.
Acknowledgments
We thank Professor Chunlei Han from Turku PET Centre for his guidance on the use of Carimas software.
Funding: None.
Footnote
Reporting Checklist: The authors have completed the TRIPOD reporting checklist. Available at https://atm.amegroups.com/article/view/10.21037/atm-22-4692/rc
Data Sharing Statement: Available at https://atm.amegroups.com/article/view/10.21037/atm-22-4692/dss
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://atm.amegroups.com/article/view/10.21037/atm-22-4692/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). This study was approved by the ethics committee of the Guangdong Provincial People’s Hospital (No. KY-Q-2022-345-01), and individual patient consent for this retrospective analysis was waived.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Villines TC, Hulten EA, Shaw LJ, et al. Prevalence and severity of coronary artery disease and adverse events among symptomatic patients with coronary artery calcification scores of zero undergoing coronary computed tomography angiography: results from the CONFIRM (Coronary CT Angiography Evaluation for Clinical Outcomes: An International Multicenter) registry. J Am Coll Cardiol 2011;58:2533-40. [Crossref] [PubMed]
- GBD 2013 Mortality and Causes of Death Collaborators. Global, regional, and national age-sex specific all-cause and cause-specific mortality for 240 causes of death, 1990-2013: a systematic analysis for the Global Burden of Disease Study 2013. Lancet 2015;385:117-71. [Crossref] [PubMed]
- Wu W, Zhang J, Xie H, et al. Automatic detection of coronary artery stenosis by convolutional neural network with temporal constraint. Comput Biol Med 2020;118:103657. [Crossref] [PubMed]
- Amsterdam EA, Wenger NK, Brindis RG, et al. 2014 AHA/ACC Guideline for the Management of Patients with Non-ST-Elevation Acute Coronary Syndromes: a report of the American College of Cardiology/American Heart Association Task Force on Practice Guidelines. J Am Coll Cardiol 2014;64:e139-e228. Erratum in: J Am Coll Cardiol 2014;64:2713-4. [Crossref] [PubMed]
- Gąsior M, Zembala MO, Tajstra M, et al. Hybrid revascularization for multivessel coronary artery disease. JACC Cardiovasc Interv 2014;7:1277-83. [Crossref] [PubMed]
- Lee W, Kim JB, Yang DH, et al. Comparative effectiveness of coronary screening in heart valve surgery: Computed tomography versus conventional coronary angiography. J Thorac Cardiovasc Surg 2018;155:1423-1431.e3. [Crossref] [PubMed]
- Zheng M, Wei M, Wen D, et al. Transluminal attenuation gradient in coronary computed tomography angiography for determining stenosis severity of calcified coronary artery: a primary study with dual-source CT. Eur Radiol 2015;25:1219-28. [Crossref] [PubMed]
- Dikkers R, Willems TP, Piers LH, et al. Coronary revascularization treatment based on dual-source computed tomography. Eur Radiol 2008;18:1800-8. [Crossref] [PubMed]
- Rosado Ingelmo A, Doña Diaz I, Cabañas Moreno R, et al. Clinical Practice Guidelines for Diagnosis and Management of Hypersensitivity Reactions to Contrast Media. J Investig Allergol Clin Immunol 2016;26:144-55; quiz 2 p following 155.
- Nash K, Hafeez A, Hou S. Hospital-acquired renal insufficiency. Am J Kidney Dis 2002;39:930-6. [Crossref] [PubMed]
- Valgimigli M, Frigoli E, Leonardi S, et al. Radial versus femoral access and bivalirudin versus unfractionated heparin in invasively managed patients with acute coronary syndrome (MATRIX): final 1-year results of a multicentre, randomised controlled trial. Lancet 2018;392:835-48. [Crossref] [PubMed]
- Berry JJ, Hoffman JM, Steenbergen C, et al. Human pathologic correlation with PET in ischemic and nonischemic cardiomyopathy. J Nucl Med 1993;34:39-47. [PubMed]
- Dilsizian V, Bacharach SL, Beanlands RS, et al. ASNC imaging guidelines/SNMMI procedure standard for positron emission tomography (PET) nuclear cardiology procedures. J Nucl Cardiol 2016;23:1187-226. [Crossref] [PubMed]
- Hajjiri MM, Leavitt MB, Zheng H, et al. Comparison of positron emission tomography measurement of adenosine-stimulated absolute myocardial blood flow versus relative myocardial tracer content for physiological assessment of coronary artery stenosis severity and location. JACC Cardiovasc Imaging 2009;2:751-8. [Crossref] [PubMed]
- Wang F, Xu W, Lv W, et al. Evaluation of the diagnostic value of joint PET myocardial perfusion and metabolic imaging for vascular stenosis in patients with obstructive coronary artery disease. J Nucl Cardiol 2021;28:3070-80. [Crossref] [PubMed]
- Sun XX, Li S, Wang Y, et al. Rescue Protocol to Improve the Image Quality of 18F-FDG PET/CT Myocardial Metabolic Imaging. Clin Nucl Med 2021;46:369-74. [Crossref] [PubMed]
- Pelletier-Galarneau M, Martineau P, El Fakhri G. Quantification of PET Myocardial Blood Flow. Curr Cardiol Rep 2019;21:11. [Crossref] [PubMed]
- Cho SG, Kim JH, Cho JY, et al. Characteristics of anginal patients with high resting myocardial blood flow measured with N-13 ammonia PET/CT. Nucl Med Commun 2015;36:619-24. [Crossref] [PubMed]
- Shu ZY, Cui SJ, Zhang YQ, et al. Predicting Chronic Myocardial Ischemia Using CCTA-Based Radiomics Machine Learning Nomogram. J Nucl Cardiol 2022;29:262-74. [Crossref] [PubMed]
- Raisi-Estabragh Z, Izquierdo C, Campello VM, et al. Cardiac magnetic resonance radiomics: basic principles and clinical perspectives. Eur Heart J Cardiovasc Imaging 2020;21:349-56. [Crossref] [PubMed]
- Gillies RJ, Kinahan PE, Hricak H. Radiomics: Images Are More than Pictures, They Are Data. Radiology 2016;278:563-77. [Crossref] [PubMed]
- Baessler B, Mannil M, Oebel S, et al. Subacute and Chronic Left Ventricular Myocardial Scar: Accuracy of Texture Analysis on Nonenhanced Cine MR Images. Radiology 2018;286:103-12. [Crossref] [PubMed]
- Ma Q, Ma Y, Yu T, et al. Radiomics of Non-Contrast-Enhanced T1 Mapping: Diagnostic and Predictive Performance for Myocardial Injury in Acute ST-Segment-Elevation Myocardial Infarction. Korean J Radiol 2021;22:535-46. [Crossref] [PubMed]
- Baessler B, Luecke C, Lurz J, et al. Cardiac MRI and Texture Analysis of Myocardial T1 and T2 Maps in Myocarditis with Acute versus Chronic Symptoms of Heart Failure. Radiology 2019;292:608-17. [Crossref] [PubMed]
- Slart RHJA, Williams MC, Juarez-Orozco LE, et al. Position paper of the EACVI and EANM on artificial intelligence applications in multimodality cardiovascular imaging using SPECT/CT, PET/CT, and cardiac CT. Eur J Nucl Med Mol Imaging 2021;48:1399-413. [Crossref] [PubMed]
- Yip SS, Aerts HJ. Applications and limitations of radiomics. Phys Med Biol 2016;61:R150-66. [Crossref] [PubMed]
- Hatt M, Le Rest CC, Tixier F, et al. Radiomics: Data Are Also Images. J Nucl Med 2019;60:38S-44S. [Crossref] [PubMed]
- Mannil M, Eberhard M, von Spiczak J, et al. Artificial Intelligence and Texture Analysis in Cardiac Imaging. Curr Cardiol Rep 2020;22:131. [Crossref] [PubMed]
- Maddahi J, Packard RR. Cardiac PET perfusion tracers: current status and future directions. Semin Nucl Med 2014;44:333-43. [Crossref] [PubMed]
- Chen C, Qin C, Qiu H, et al. Deep Learning for Cardiac Image Segmentation: A Review. Front Cardiovasc Med 2020;7:25. [Crossref] [PubMed]
- Harms HJ, Nesterov SV, Han C, et al. Comparison of clinical non-commercial tools for automated quantification of myocardial blood flow using oxygen-15-labelled water PET/CT. Eur Heart J Cardiovasc Imaging 2014;15:431-41. [Crossref] [PubMed]
- Nesterov SV, Han C, Mäki M, et al. Myocardial perfusion quantitation with 15O-labelled water PET: high reproducibility of the new cardiac analysis software (Carimas). Eur J Nucl Med Mol Imaging 2009;36:1594-602. [Crossref] [PubMed]
- Manabe O, Ohira H, Hirata K, et al. Use of 18F-FDG PET/CT texture analysis to diagnose cardiac sarcoidosis. Eur J Nucl Med Mol Imaging 2019;46:1240-7. [Crossref] [PubMed]
- Zhang R, Zhang Q, Ji A, et al. Identification of high-risk carotid plaque with MRI-based radiomics and machine learning. Eur Radiol 2021;31:3116-26. [Crossref] [PubMed]
- Leopold JA, Maron BA, Loscalzo J. The application of big data to cardiovascular disease: paths to precision medicine. J Clin Invest 2020;130:29-38. [Crossref] [PubMed]
- Ngiam KY, Khor IW. Big data and machine learning algorithms for health-care delivery. Lancet Oncol 2019;20:e262-73. [Crossref] [PubMed]
- Al'Aref SJ, Maliakal G, Singh G, et al. Machine learning of clinical variables and coronary artery calcium scoring for the prediction of obstructive coronary artery disease on coronary computed tomography angiography: analysis from the CONFIRM registry. Eur Heart J 2020;41:359-67. [Crossref] [PubMed]
- Al'Aref SJ, Anchouche K, Singh G, et al. Clinical applications of machine learning in cardiovascular disease and its relevance to cardiac imaging. Eur Heart J 2019;40:1975-86. [Crossref] [PubMed]
- Song Y, Zhang J, Zhang YD, et al. FeAture Explorer (FAE): A tool for developing and comparing radiomics models. PLoS One 2020;15:e0237587. [Crossref] [PubMed]
- Guyon I, Weston J, Barnhill S, et al. Gene Selection for Cancer Classification using Support Vector Machines. Machine Learning 2002;46:389-422. [Crossref]
- Tang J, Wang Y, Luo Y, et al. Computational advances of tumor marker selection and sample classification in cancer proteomics. Comput Struct Biotechnol J 2020;18:2012-25. [Crossref] [PubMed]
- Zhang Y, Cheng C, Liu Z, et al. Radiomics analysis for the differentiation of autoimmune pancreatitis and pancreatic ductal adenocarcinoma in 18 F‐FDG PET/CT. Med Phys 2019;46:4520-30. [Crossref] [PubMed]
- Umutlu L, Nensa F, Demircioglu A, et al. Radiomics Analysis of Multiparametric PET/MRI for N- and M-Staging in Patients with Primary Cervical Cancer. Rofo 2020;192:754-63. [Crossref] [PubMed]
- Xu X, Zhang X, Tian Q, et al. Quantitative Identification of Nonmuscle-Invasive and Muscle-Invasive Bladder Carcinomas: A Multiparametric MRI Radiomics Analysis. J Magn Reson Imaging 2019;49:1489-98. [Crossref] [PubMed]
- Yong AS, Daniels D, De Bruyne B, et al. Fractional flow reserve assessment of left main stenosis in the presence of downstream coronary stenoses. Circ Cardiovasc Interv 2013;6:161-5. [Crossref] [PubMed]
- Klumpp B, Miller S, Seeger A, et al. Is the diagnostic yield of myocardial stress perfusion MRI impaired by three-vessel coronary artery disease? Acta Radiol 2015;56:143-51. [Crossref] [PubMed]
- Djordjevic Dikic A, Tesic M, Boskovic N, et al. Prognostic Value of Preserved Coronary Flow Velocity Reserve by Noninvasive Transthoracic Doppler Echocardiography in Patients With Angiographically Intermediate Left Main Stenosis. J Am Soc Echocardiogr 2019;32:74-80. [Crossref] [PubMed]
- Abaci A, Oğuzhan A, Kahraman S, et al. Effect of diabetes mellitus on formation of coronary collateral vessels. Circulation 1999;99:2239-42. [Crossref] [PubMed]
- Eftekhari A, Min J, Achenbach S, et al. Fractional flow reserve derived from coronary computed tomography angiography: diagnostic performance in hypertensive and diabetic patients. Eur Heart J Cardiovasc Imaging 2017;18:1351-60. [Crossref] [PubMed]
- Liga R, Rovai D, Sampietro T, et al. Insulin resistance is a major determinant of myocardial blood flow impairment in anginal patients. Eur J Nucl Med Mol Imaging 2013; Epub ahead of print. [Crossref] [PubMed]


