Patient-specific finite element modeling for fracture risk prediction in a canine model of osteosarcoma
Highlight box
Key findings
• The study showed no significant differences between experimental and finite element (FE) data for stiffness, strain, and yield load, supporting the validity of the FE technique.
What is known and what is new?
• Fracture risk prediction in patients with bone tumors is currently based on semi-qualitative methods that don’t consider the patient’s specific bone geometry.
• This study develops a FE technique that can create patient-specific models based on computed tomography scans. These models can be tested under a variety of loading conditions to determine the patient’s risk of fracture.
What is the implication, and what should change now?
• Clinicians can use this predicted fracture risk to make more informed treatment decisions for the patient, especially regarding whether surgical intervention is necessary.
Introduction
Background
Pathological fractures due to bone metastases are a significant challenge for patients suffering from advanced stages of cancer. Fracture incidence rates are highest among those with multiple myeloma, breast, and prostate cancer (43%, 35%, and 19% respectively) (1). Complications arising from pathological fractures have been found to increase mortality risk (1,2); for breast cancer patients in particular, fractures have been associated with a 32% higher risk of death (1). Bone tumors can also be caused by primary bone cancer, such as osteosarcoma, where the cancer originates in the bone. Though more prevalent in animals than humans, osteosarcoma causes similar symptoms and tumor structure to bone metastases (3). Typical treatments for bone tumors include radiotherapy, internal fixation (such as plates and intramedullary nails), and amputation (4,5). Choosing the ideal treatment depends heavily on the patient’s fracture risk; unfortunately, this risk is often uncertain, and doctors are forced to base treatment plans on qualitative guidelines developed from retrospective analyses of similar tumors (6). One of the most common guidelines is the Mirels’ classification, which considers size, site, and nature of the lesion, along with pain level. With the Mirels’ classification, a numerical score of 1–3 is given to each of these metrics, and the sum of scores is used to advise treatment (7). The drawback of this method is the lack of patient-specific, quantitative data, particularly for borderline scores where it’s unclear where radiotherapy or surgical intervention is the best treatment.
Rationale and knowledge gap
One way to quantify fracture risk is through the creation of patient-specific finite element (FE) models that are capable of predicting bone fracture mechanics. The basis of the FE method lies in breaking a large numerical problem, in this scenario the mechanics of an entire limb, into many, much smaller and computationally simpler numerical problems, referred to as elements. To create an accurate FE model, computed tomography (CT) scans can be collected from the patient and converted to a geometrically accurate FE computer model composed of elements, each with unique properties related to the corresponding CT scan density. This allows for close replication of bone geometry and heterogenous material properties (8). By applying physiologically relevant forces to the model and observing stresses within the bone, predictions can be made regarding the probability of bone fracture, providing a quantitative assessment tool relative to the semi-qualitative and more general technique currently used, greatly benefiting the patient. In the case of bone cancer, preemptive surgical intervention can help stabilize the bone if the model predicts fracture. If bone fracture is not predicted, then the patient is spared unnecessary surgical treatment (9).
FE modeling has been used previously for orthopedic bone characterization and fracture prediction applications. Many studies have focused on long bones such as the femur or humerus (8-10), while others have modeled irregular bones like spinal vertebrae (11). Some studies have also modeled metastatic lesions from human cadaveric tissue (12,13). To our knowledge, no previous FE studies have been done on a canine osteosarcoma model. All of these previous studies use a similar procedure of transforming CT scans into FE models and assigning material properties, with the main differences being element size and material definition. One method of defining materials in the model is to identify separate regions within the bone (cortical, trabecular, and marrow) and specifying a homogeneous elastic modulus in each region, typically derived from population averages (14). This approach generally lacks the accuracy of more refined techniques and is not suitable for patient-specific applications. The second method is to use Hounsfield units from the CT scan to define bone density and elastic modulus from predetermined linear relationships, resulting in a model with heterogenous material properties that can account for differences in elastic modulus between trabecular and cortical bone. The main drawback of this method is that the density relationships are derived only for bone and can’t necessarily be extrapolated for use in soft tissue such as bone marrow. However, since long bone mechanics are heavily dominated by cortical bone material strength with little contribution from soft tissue constituents, simplification of these soft tissue properties do not greatly affect model accuracy.
Many previous models have not demonstrated large-scale clinical validation. Due to the relatively greater prevalence of osteosarcoma in canines (15) as compared to humans, a canine model was used in this study to leverage the patient population as a means of expedited clinical validation of the fracture prediction model. The canine osteosarcoma model will serve as a preliminary model to validate the procedure before moving on to testing with lesions and human tissue. The benefit of starting with canines is that the modeling procedure could eventually be tested on living canine patients to determine whether it’s clinically feasible and allow for making appropriate changes to the technique necessary to be useful in humans.
Objective
To address the need of improved long bone fracture prediction for cancer patients, the aim of this study was to develop and validate an FE technique capable of predicting fracture using a canine radius model. This model was chosen due to the prevalence of osteosarcoma in large dog breeds (15).
Methods
Sample preparation
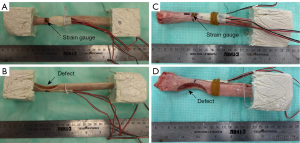
Eight healthy radii from three right limbs and five left limbs were collected from canine patients euthanized for unrelated reasons. Because this study used cadaver tissues and no in vivo experiments, review by an Animal Care and Use Committee was not required. Breeds included four Great Danes, two Great Pyrenees, one Rottweiler, and one Mastiff with a mean patient mass of 67.4 kg and standard deviation of 18.4 kg. To model the effect of a sarcoma, semicircular osteotomies were created at the distal end of each radius using a crescentic oscillating saw (Figure 1). Osteotomy size varied based on the width of the individual radii, with half of the bone width being removed at the thinnest point of the defect (Figure 1B,1D). Samples subsequently underwent CT scans (Siemens Somatom Definition AS 64-slice scanner, SIEMENS Healthineers, Munich, Germany) at 1 mm slice resolution and were randomly allocated to one of three loading groups for biomechanical testing: cantilever bending (n=3, sample IDs B1–B3), torsion (n=3, sample IDs T1–T3), and compression (n=2, sample IDs C1,C2).
Mechanical testing
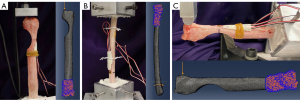
All samples were potted in quick-cure resin (Smooth-Cast 320; Smooth-On, Inc., Macungie, PA, USA) at the proximal end of the bone away from the osteotomy defect. Torsion samples were additionally potted distal to the osteotomy. For compression and bending tests, the distal end of the bone remained unfixed. Before potting, three wood screws were inserted in the regions marked for fixation to prevent slippage of the radii within the resin. Rosette strain gauges (Tokyo Measuring Instruments Laboratory Co., Ltd., Tokyo, Japan) were then attached to the periosteal surface of the bone directly opposite the osteotomy where bone stress was anticipated to be greatest (Figure 1A,1C). Samples were loaded in a servohydraulic testing machine (MTS Landmark; MTS System Corp., Eden Prairie, MN, USA) according to their allotted treatment group (Figure 2A-2C) and destructive biomechanical tests were performed to failure at a loading rate of 0.1 mm/s or 0.5 degrees/s. Outcome parameters included stiffness (compressive, bending, or torsional), strain, and yield load or torque.
FE modeling
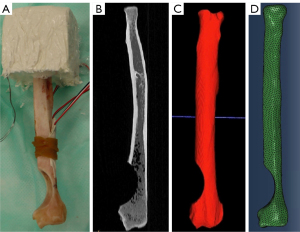
Patient-specific FE models were created for each bone by using individual CT scans and replicating the corresponding biomechanical loading conditions for each sample (Figure 3). CT scans were uploaded to ITK Snap (Penn Image Computing and Science Laboratory, Philadelphia, PA, USA) for 3D segmentation (Figure 3B). Initial segmentation was performed automatically, followed by manual segmentation to fill gaps and smooth surfaces (Figure 3C). Resulting surface meshes were further refined in MeshLab (ISTI-CNR Research Center, Pisa, Italy) using a surface reconstruction with a voxel size of 1.0mm. Final meshes were created using Coreform Cubit (Coreform, Orem, UT, USA) using tetrahedral elements (Figure 3D). Models had an average of 338,300 elements and 431,200 nodes, with element sides having a maximum length of 1 mm. A mesh convergence analysis was performed, and this element size of 1 mm was determined to be converged (within 1% difference in strain and strain energy from a 0.75 mm mesh).
Material properties were assigned in the software Bonemat (Insituto Ortopedico Rizzoli, Bologna, Italy) using previously established relationships between CT scan Hounsfield units (HU), bone density (ρ), and elastic modulus (E) in canine bone as seen in {Eqs. [1,2]} (8).
Both the tetrahedral mesh and CT scan DICOM files were uploaded to Bonemat and aligned to ensure that the generated material properties were accurate relative to location in the bone. Because these equations were applied to the entire model and not regionally within the bone, medullary cavity elastic modulus was manually input as a constant isotropic value of 0.02 MPa (16). The medullary cavity was defined using an HU cutoff for bone of 226 HU, corresponding to an elastic modulus of 2,462 MPa. All regions in the model with a modulus lower than this were considered to be part of the medullary cavity; this was confirmed by visual inspection of these regions. This proposed method of defining materials was compared to two other possibilities: solely using Eqs. [1,2] for the entire model, and neglecting bone marrow by removing all material within the medullary cavity. The proposed method was determined to be the most accurate of the three.
All models were uploaded to Abaqus (2020, Dassault Sytemes, Velizy-Villacoublay, France) for FE analysis. Element geometric order was changed from linear to quadratic while keeping the tetrahedral element type. Locations of potting resin, strain gages, and load points were determined via image analysis of photographs taken during mechanical testing. Boundary conditions were added to each model to simulate potting fixation (fixed displacement and rotation in all directions) at the distal end of the bone using an Encastre boundary condition. Loads were then added according to the corresponding biomechanical testing treatment group where all load magnitudes were set to the corresponding yield load or torque value determined during testing. For compression, an axial point load was applied to a 2 mm2 area at the most proximal aspect of the bone. For bending samples, the point load was oriented perpendicular to the long axis of the bone. For torsion samples, a pure moment was applied to the proximal potting region via a coupling constraint.
Analysis was performed on each model to determine output parameter values. Stiffness data were generated from the slope of force-displacement curves up to experimental yield values. Strain was taken as an average of the maximum principal strain (εmax) for seven surface elements at the location of the strain gage. Yield load from the model was predicted using a maximum principal strain-based criterion (10) assuming bone failure in tension {Eqs. [3,4]}. The threshold strain for this criterion was 0.0073, which is the yield strain of human bone in tension (10) and has been used in previous canine studies (8). This criterion was used as it was determined to be more conservative than stress-based yield criteria (17).
Statistical analysis
Statistical comparisons were not performed between experimental and computational results due to the limited sample size in each loading group (N=3 for bending, N=3 for torsion, and N=2 for compressions). To assess how well the FE models predicted experimental results, linear regressions were performed on predicted yield load versus experimental yield load. Regressions with R2 values close to one indicate good correlation between results.
Results
Experimental results
Fracture modes for each specimen followed trends according to mechanical loading type (Figure 4). Both compression samples failed via oblique fractures at the osteotomy; C1 demonstrated a clear oblique fracture (Figure 4D), and C2 failed by an oblique fracture with an additional transverse fracture proximal to the main fracture (Figure 4C). All torsion samples failed via a spiral fracture starting at the osteotomy that traveled proximally along the bone (Figure 4B). All bending samples splintered at the thinnest point of the osteotomy (Figure 4A). Quantitative results are summarized in Table 1. Yield loads for individual samples were 867 N (C1), 1,028 N (C2), 157 N (B1), 403 N (B2), 471 N (B3), 7.7 N·m (T1), 5.0 N·m (T2), and 3.8 N·m (T3).
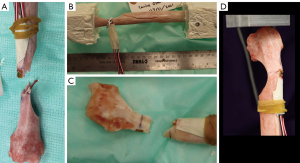
Table 1
| Loading type | Stiffness | Maximum principal strain (µe) at osteotomy |
Yield load/torque |
|---|---|---|---|
| Bending (N=3) | 28.9±13.9 N/mm | 9,502±2,018 | 343±135 N |
| Torsion (N=3) | 16.9±8.5 N·mm/rad | 5,197±343 | 5.50±1.61 N·m |
| Compression (N=2) | 421±116 N/mm | 5,354±652 | 947±81 N |
Data are presented as means ± standard deviations.
FE results
Comparisons of individual sample data are illustrated in Figures 5,6, and Table 2. The FE models accurately predicted stiffness, with all samples having less than 7.5% error and three samples within a 1% error. Plots of linear regressions are shown in Figure 7 for bending and compression (Figure 7A) and for torsion (Figure 7B). The respective R2 values were 0.9335 and 0.8798.
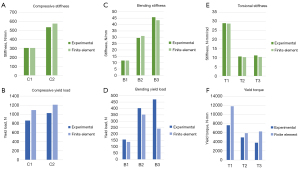
Table 2
| Error type | Bending | Torsion | Compression | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| B1 | B2 | B3 | T1 | T2 | T3 | C1 | C2 | |||
| Stiffness error (%) | 0.34 | 5.3 | −5.2 | −0.72 | −2.7 | −7.3 | 0.03 | 7.3 | ||
| Strain error (%) | −1.9 | 7.4 | 15.1 | −11.1 | 10.7 | −6.2 | −3.9 | 31.6 | ||
| Yield load error (%) | −11.5 | −12.5 | −48.6 | 54.2 | 19.0 | 64.6 | 26.5 | 18.0 | ||

Discussion
Overall, the FE model was most accurate in predicting stiffness, followed by strain, with yield load having the lowest accuracy. Some of the error in the strain-based yield load predictions likely resulted because the location of the fracture did not occur at the region of interest (ROI) (location of strain gauge measurements) in all samples, particularly for torsion samples. Furthermore, strain values in the FE model changed considerably with slight movements in ROI location, so any error accumulated by image analysis of ROI location and manual ROI placement within the model may have resulted in increased errors in strain data accuracy. It is clear that exact replication of the experimental and model strain measurement areas is critical when making these predictions. On the other hand, the force and displacement data used to calculate stiffness was less sensitive to the exact placement of the point load and more sensitive to the angle of the load. Because all loads were directly aligned with a coordinate axis, it was relatively easy to ensure load alignment in the FE model, therefore minimizing error in stiffness predictions.
When loaded under compression, samples generally yielded at a higher load and exhibited greater stiffness than the other loading types, which is consistent with data published by Hart et al. (18). Maximum principal strain, measured at the thinnest point of the osteotomy, was highest in bending, while torsion and compression resulted in similar values.
Ultimately, this modeling procedure meets the goal of providing a method to predict fracture in cancer patients better than current clinical semi-qualitative methods. While the Mirels’ scoring system may be sufficient in determining treatment type for patients with minor or severe tumors, decisions regarding moderate tumors are made solely based on clinical judgment (7). Although some deep learning methods are being developed to predict fracture better than Mirels’ (19,20), these still base their analysis on similar tumors, and not patient-specific tumor properties. The accuracy of the models in this study would provide helpful, patient-specific numerical data for such tumors so that the doctor can more confidently assess the severity of fracture risk.
Evaluating a clinical example can be useful in the context of this study. Peak compression forces in a canine forelimb when jumping from a height of 0.65 m have been measured to be 30.84±3.66 N/kg (21), which is meant to represent a dog jumping from a vehicle tailgate. Using the average canine mass in this study of 67.4 kg, this results in a force of 2,078±247 N. Based on the predicted yield load for the two compression samples (1,097 and 1,212 N), both samples would have failed in this loading scenario (actual yield loads of 867 and 1,028 N support this conclusion). This example shows how the proposed FE model could be used to predict fracture likelihood in a canine patient based on common physiological loads. The same technique could be applied to human patients once the model has been validated on human tissue. With this knowledge, clinicians could make more informed decisions regarding ideal treatment for the patient.
Results from this study were compared to similar fracture prediction studies. When performing a linear regression on the relationship between experimental and FE-predicted yield, R2 values of 0.94 for compression/bending and 0.88 for torsion were observed. These values are similar to previous research that used CT-based FE models to assess fracture likelihood in metastatic femurs which reported R2 values of 0.90 and 0.93 for intact bones and bone with lesions, respectively (12). Two separate groups utilized similar FE methods in femurs and reported R2 correlations of 0.78 (22) and 0.88 (23). This suggests that the proposed modeling procedure possesses similar accuracy to other published methods.
The modeling procedure of this study mainly differed from other CT-based FE models in the definition of material property. Stadelmann et al. set a constant elastic modulus (10 GPa) for their publication on human vertebrae (13), while others used HU and density equations to calculate modulus without considering the effect of bone marrow on mechanics (24,25). The technique outlined in this study used similar equations for bone (though for canine rather than human) but set bone marrow modulus to a constant value. When investigating methods of applying material properties, it was found that using these equations for the whole model (including the medullary cavity) had a 30% higher error than proposed method, while neglecting bone marrow had a 38% higher error. This suggests that bone marrow does affect bone mechanics and should be accounted for.
This study had several limitations that could affect the overall accuracy and usefulness of the results. The main limitation was that this study had a small sample size; additional samples are needed in future studies to support validation of the models more robustly. Another major limitation of this procedure is the amount of manual input required to develop these models, which allows for some slight variation in properties between models, and increases the time required to test a model. These drawbacks limit this method’s usefulness in clinical applications, as model creation would require trained personnel and may increase patient costs. However, now that the technique has been validated, this problem may be addressed in future studies by implementing automation for segmentation, meshing, and material assignment. The need for CT scanning currently also limits clinical feasibility, as this isn’t always the standard of care for patients with bone tumors (plain radiographs are more commonly used). However, the prevalence of CT scanning in this population may increase as more diagnostic computational modeling technology becomes available. Second, this study utilizes simple loading conditions, whereas bones in vivo are subject to complex combined loading that include combinations of compression, bending, and torsional loading. Further research is needed to quantify how these combined loads affect bone yield load magnitudes and strains. Finally, this study utilized simplified osteotomy defects to represent osteosarcoma lesions. Although the osteotomy simulates the weakening of the bone that occurs in active lesions, it does not take into account structural and material properties of the tumor. Future work will further investigate the use of FE models on limbs with clinically diagnosed osteosarcoma to better represent the effect of tumors on fracture mechanics. Once validated, this model could also be used to test the effect of fixation such as plates or intramedullary nails that may optimize patient limb strength and surgical invasiveness.
Conclusions
In conclusion, the FE technique presented in this study shows promising accuracy in predicting bone fracture mechanics in canine radii with artificial osteosarcoma defects. Although more work is needed in order to translate to humans, this method could eventually provide clinicians with quantitative data to support decisions regarding surgical intervention for patients with osteosarcoma or bone metastases.
Acknowledgments
Funding: None.
Footnote
Data Sharing Statement: Available at https://atm.amegroups.com/article/view/10.21037/atm-23-1699/dss
Peer Review File: Available at https://atm.amegroups.com/article/view/10.21037/atm-23-1699/prf
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://atm.amegroups.com/article/view/10.21037/atm-23-1699/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. Because this study used cadaver tissues and no
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Saad F, Lipton A, Cook R, et al. Pathologic fractures correlate with reduced survival in patients with malignant bone disease. Cancer 2007;110:1860-7. [Crossref] [PubMed]
- Salunke AA, Chen Y, Tan JH, et al. Does a pathological fracture affect the prognosis in patients with osteosarcoma of the extremities?: a systematic review and meta-analysis. Bone Joint J 2014;96-B:1396-403. [Crossref] [PubMed]
- Macedo F, Ladeira K, Pinho F, et al. Bone Metastases: An Overview. Oncol Rev 2017;11:321. [Crossref] [PubMed]
- Willeumier JJ, van der Linden YM, van de Sande MAJ, et al. Treatment of pathological fractures of the long bones. EFORT Open Rev 2016;1:136-45. [Crossref] [PubMed]
- Ehne J, Tsagozis P. Current concepts in the surgical treatment of skeletal metastases. World J Orthop 2020;11:319-27. [Crossref] [PubMed]
- Damron TA, Mann KA. Fracture risk assessment and clinical decision making for patients with metastatic bone disease. J Orthop Res 2020;38:1175-90. [Crossref] [PubMed]
- Jawad MU, Scully SP. In brief: classifications in brief: Mirels' classification: metastatic disease in long bones and impending pathologic fracture. Clin Orthop Relat Res 2010;468:2825-7. [Crossref] [PubMed]
- Laurent CP, Böhme B, Mengoni M, et al. Prediction of the mechanical response of canine humerus to three-point bending using subject-specific finite element modelling. Proc Inst Mech Eng H 2016;230:639-49. [Crossref] [PubMed]
- Benca E, Synek A, Amini M, et al. QCT-based finite element prediction of pathologic fractures in proximal femora with metastatic lesions. Sci Rep 2019;9:10305. [Crossref] [PubMed]
- Yosibash Z, Tal D, Trabelsi N. Predicting the yield of the proximal femur using high-order finite-element analysis with inhomogeneous orthotropic material properties. Philos Trans A Math Phys Eng Sci 2010;368:2707-23. [Crossref] [PubMed]
- Dreischarf M, Zander T, Shirazi-Adl A, et al. Comparison of eight published static finite element models of the intact lumbar spine: predictive power of models improves when combined together. J Biomech 2014;47:1757-66. [Crossref] [PubMed]
- Derikx LC, van Aken JB, Janssen D, et al. The assessment of the risk of fracture in femora with metastatic lesions: comparing case-specific finite element analyses with predictions by clinical experts. J Bone Joint Surg Br 2012;94:1135-42. [Crossref] [PubMed]
- Stadelmann MA, Schenk DE, Maquer G, et al. Conventional finite element models estimate the strength of metastatic human vertebrae despite alterations of the bone's tissue and structure. Bone 2020;141:115598. [Crossref] [PubMed]
- Poelert S, Valstar E, Weinans H, et al. Patient-specific finite element modeling of bones. Proc Inst Mech Eng H 2013;227:464-78. [Crossref] [PubMed]
- Anfinsen KP, Grotmol T, Bruland OS, Jonasdottir TJ. Breed-specific incidence rates of canine primary bone tumors--a population based survey of dogs in Norway. Can J Vet Res 2011;75:209-15.
- Jansen LE, Birch NP, Schiffman JD, et al. Mechanics of intact bone marrow. J Mech Behav Biomed Mater 2015;50:299-307. [Crossref] [PubMed]
- Schileo E, Taddei F, Cristofolini L, et al. Subject-specific finite element models implementing a maximum principal strain criterion are able to estimate failure risk and fracture location on human femurs tested in vitro. J Biomech 2008;41:356-67. [Crossref] [PubMed]
- Hart NH, Nimphius S, Rantalainen T, et al. Mechanical basis of bone strength: influence of bone material, bone structure and muscle action. J Musculoskelet Neuronal Interact 2017;17:114-39.
- Vandenput L, Johansson H, McCloskey EV, et al. Update of the fracture risk prediction tool FRAX: a systematic review of potential cohorts and analysis plan. Osteoporos Int 2022;33:2103-36. [Crossref] [PubMed]
- Kong SH, Lee JW, Bae BU, et al. Development of a Spine X-Ray-Based Fracture Prediction Model Using a Deep Learning Algorithm. Endocrinol Metab (Seoul) 2022;37:674-83. [Crossref] [PubMed]
- Pardey D, Tabor G, Oxley JA, et al. Peak forelimb ground reaction forces experienced by dogs jumping from a simulated car boot. Vet Rec 2018;182:716. [Crossref] [PubMed]
- Yosibash Z, Plitman Mayo R, et al. Predicting the stiffness and strength of human femurs with real metastatic tumors. Bone 2014;69:180-90. [Crossref] [PubMed]
- Keyak JH, Kaneko TS, Tehranzadeh J, et al. Predicting proximal femoral strength using structural engineering models. Clin Orthop Relat Res 2005;219-28. [Crossref] [PubMed]
- Sternheim A, Giladi O, Gortzak Y, et al. Pathological fracture risk assessment in patients with femoral metastases using CT-based finite element methods. A retrospective clinical study. Bone 2018;110:215-20. [Crossref] [PubMed]
- Goodheart JR, Cleary RJ, Damron TA, et al. Simulating activities of daily living with finite element analysis improves fracture prediction for patients with metastatic femoral lesions. J Orthop Res 2015;33:1226-34. [Crossref] [PubMed]