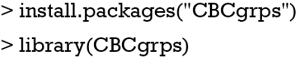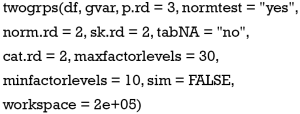Comparing baseline characteristics between groups: an introduction to the CBCgrps package

Introduction

Electronic healthcare records (EHR), which contain digital healthcare information from routine clinical practice for individuals with relatively large sample sizes, are an important source of data to explore potential association between diseases of interest and possible causative variables. However, one of the problems researchers may encounter is the a large number of variables being analyzed (1,2). In addition, some identified associated variables contributed to disease may be overestimated due to the curse of high dimensionality and computational complexity (3), and also some may be underestimated and are false negatives due to confounding factors or other biases. There is no panacea for all these problems. However, One way of solution is to make use of big-data with more reliable and complete information obtained from EHR systems, in which statistical patterns could be modelled for testing effectively and efficiently associations between multiple variables and diseases of interest based on machine-learning techniques, including supervised and unsupervised learning (4).

The availability of EHR makes big data mining possible, which typically involves a large number of variables to be explored. The first step of data mining usually involves statistical description and bivariate statistical inference (5). The Strengthening the Reporting of Observational Studies in Epidemiology (STROBE) Statement also recommends reporting descriptive data in the result section. Item 14 in the STROBE checklist mandates an observational study to “give characteristics of study participants (e.g. demographic, clinical, social) and information on exposures and potential confounders ” (6). Since observational studies are subject to confounding bias, adjusted analyses with regression modeling or other matching techniques are usually mandatory (7). A usual practice in observational studies is the comparison of baseline characteristics of participants between study groups. The overall population can be grouped by clinical outcome or exposure status. A combined table reporting baseline characteristics is usually displayed, for the overall population and then separately for each group. The last column usually gives the P value for the comparison between study groups. In the conventional research model, the variables for which data are collected are limited in number. It is thus feasible to calculate descriptive data one by one and to manually create the table. The availability of EHR and big data mining techniques makes it possible to explore a far larger number of variables. However, manual tabulation of big data is particularly error prone; it is exceedingly time-consuming to create and revise such tables manually. In this paper, we introduce an R package called CBCgrps, which is designed to automate and streamline the generation of such tables when working with big data.

There is a more user-friendly tutorial displayed in html format (supplemental file, created by J Wang, available online: http://atm.amegroups.com/public/addition/atm/supp-atm.2017.09.39.html). In this tutorial, the distributions of continuous variables are examined using histograms. It also introduces an alternative way to produce paper-style tables by first saving the table results as Excel, then copying them to the Word processor.

The CBCgrps package

The package has been updated to version 2.1, which includes a function to generate tables comparing three or more groups. In the older version (version 1.0), there is only one function cbcgrps() for comparing two groups. Version 2.0 includes two such functions, twogrps() and multigrps(). The twogrps() function in version 2.0 is the same as the cbcgrps() function in version 1.0. The latest package (version 2.1) can be installed and loaded to the workspace with the following code.

Simulated dataset

There is a simulated dataset called df in the CBCgrps package. The dataset contains 1,000 observations of seven variables. C-reactive protein (crp) is a numeric vector and its value is measured in mg/L. The variable hb is hemoglobin measured in g/dL. This dataset is for the purpose of demonstration only and contains randomly generated data. The variable ddimer stands for D-dimer, which is a measurement of coagulation system. The variable wbc is for white blood cell, which is associated with systemic inflammatory response. The variable comorbid is a factor variable representing comorbidities of a patient. Sex is also a factor variable with two levels male and female. The variable mort is a measure of mortality outcome which has two levels: alive and dead. We now take a look at the structure of the dataset.

The twogrps() function

Arguments of the twogrps() function is shown below:

The first argument df receives a data frame containing variables being compared and the grouping variable. The gvar argument receives a string corresponding to the grouping variable. The p.rd argument defines the number of significant digits for the P values to be displayed in the table, with a default of 3 decimal places. The normtest argument controls whether or not to perform a test of normality. The rationale for not testing for normality is that for datasets with a large sample size, the Anderson-Darling test can be very sensitive to a small deviation from the normal distribution (8). But in real research practice, such a small deviation is generally not meaningful. In other words, huge samples can make the insignificant significant. In this circumstance, one may wish to switch off the normality testing and still use mean and standard deviation to describe the data.

The arguments norm.rd and sk.rd control the number of significant digits for the normal and skewed data, respectively. The dataset may contain missing or NA values. By default, these are removed when calculating percentages for factor variables. Missing or NA values can be included in calculations by setting tabNA="ifany". The cat.rd argument controls the number of significant digits for the proportion of factor variables.

The maxfactorlevels defines the maximum number of levels for factor variables. If there are too many levels, it reports a warning message. This is useful for suppressing calculation of date or time variables. Sometimes, categorical variables may be encoded as integer values; for example, male as 1 and female as 2. In such cases R automatically treats the gender variable as a numeric variable, and calculates the mean and standard deviation. By setting the minfactorlevels argument to 10, the function will consider numeric variables with less than 10 values to be categorical variables.

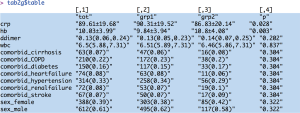
Fisher’s exact test is the accepted criteria for comparing two independent proportions in the case of small samples (9,10). However, Fisher’s exact test takes a lot of workspace thereby requiring an expansion of the workspace used in the network algorithm. By default, the workspace is “2e+05”; this may be expanded to “2e+07”. The sim argument is a logical value, taking either true or false. This indicates whether P values should be computed in Monte Carlo simulation, for tables larger than 2 by 2 (11). The returned object from twogrps() function is shown in Table 1.

Table 1 Returned object from the twogrps() function
Full table

The example

The R code for performing statistical descriptions and comparisons is extremely simple with one line of code.

The returned object of the twogrps() function is a list containing data frames. The first element $table is a data frame gathering all types of variables together. The mean and standard deviation are put in a single cell, and connected by plus and minus (±) symbol. The interquartile range is put in parenthesis and separated by a coma. Categorical variables are presented as the number and proportion. If you don’t want descriptive statistics being combined in a single cell, they can be displayed separately. The following is an example containing descriptive statistics for normal data.

Comparisons between multiple groups can be performed with the multigrps() function.

The output tables are too wide to be displayed because there are seven groups. Interpretation of the output is similar to that obtained from the twogrps() function.

Converting R output to publication-style table in Microsoft Word processor

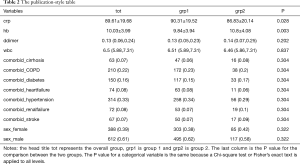
The output displayed on R console can be converted to publication-style tables in Microsoft Word. Figure 1 shows the output in R console, highlighted in light blue due to having been selected. Initially, when this output is copied and pasted into MS Word (Figure 2) it appears quite messy! However, the process to convert this into publication-ready tables is quite simple using MS Word (Figure 3). Double quotes separate columns of text. And you can remove any blank columns as needed. The final table is shown in Table 2. In this process, the table is created automatically, which is time-saving and can avoid potential errors induced by manual data input.

Figure 1 The output in R console is selected that the texts are highlighted in light blue.

Figure 2 Copy and paste the selected texts onto the Microsoft Word. It appears messy and does not conform to the publication-style of most medical journals.

Figure 3 Screen shot of the “Convert text to table” function in Word. The texts are separated at double quotes symbol (arrow).

Table 2 The publication-style table
Full table

Acknowledgements

Funding: The study was funded by Zhejiang Engineering Research Center of Intelligent Medicine (2016E10011) from the First Affiliated Hospital of Wenzhou Medical University.

Footnote

Conflicts of Interest: The authors have no conflicts of interest to declare.

References

1. Wu PY, Cheng CW, Kaddi C. Advanced Big Data Analytics for -Omic Data and Electronic Health Records: Toward Precision Medicine. IEEE Trans Biomed Eng 2016;64:263-73. [Crossref] [PubMed]
2. Butte AJ. Big data opens a window onto wellness. Nat Biotechnol 2017;35:720-1. [Crossref] [PubMed]
3. Bourgon R, Gentleman R, Huber W. Independent filtering increases detection power for high-throughput experiments. Proc Natl Acad Sci U S A 2010;107:9546-51. [Crossref] [PubMed]
4. Jensen PB, Jensen LJ, Brunak S. Mining electronic health records: towards better research applications and clinical care. Nat Rev Genet 2012;13:395-405. [Crossref] [PubMed]
5. Zhang Z. Univariate description and bivariate statistical inference: the first step delving into data. Ann Transl Med 2016;4:91. [Crossref] [PubMed]
6. von Elm E, Altman DG, Egger M, et al. Strengthening the Reporting of Observational Studies in Epidemiology (STROBE) statement: guidelines for reporting observational studies. BMJ 2007;335:806-8. [Crossref] [PubMed]
7. Harrell FE. Regression Modeling Strategies. New York, NY: Springer New York, 2001.
8. Nelson LS. The Anderson-Darling test for normality. Journal of Quality Technology 1998;30:298-9.
9. Andrés AM, Del Castillo JD. P-values for the Optimal Version of Fisher's Exact Test in the Comparison of Two Independent Proportions. Biometrical Journal 1990;32:213-27. [Crossref]
10. Camilli G. The relationship between Fisher’s exact test and Pearson’s chi-square test: A Bayesian perspective. Psychometrika 1995;60:305-12. [Crossref]
11. Campbell I. Chi-squared and Fisher-Irwin tests of two-by-two tables with small sample recommendations. Stat Med 2007;26:3661-75. [Crossref] [PubMed]