The difference in stereoacuity testing: contour-based and random dot-based graphs at far and near distances

Introduction

Stereopsis enables depth to be judged precisely. Many methods are used to test stereopsis; however, the results differ when using different applications which results in a poor correlation between the different stereo tests. The cause of this inconsistency in results may be due to the different size, shape, and familiarity of the test symbols, difference in viewing distance, or the use of spectacles (1). Two types of test graphs commonly used in clinical stereopsis testing are contour-based [e.g., Titmus circle test (2)] and random dot-based [e.g., TNO test (3), Lang stereo test (4)]. The former stereopsis tests are called “local stereopsis”, while the latter tests are called “global stereopsis”. As the measurements are all based on different disparities, the neural processing may be different. Fawcett (5) found that stereoacuity scores of healthy participants using Titmus circles, Randot circles, and Preschool Randot (random dot) did not differ significantly. However, the Titmus and Randot circle tests produced better stereoacuity results compared to the random dot-based Randot Preschool Stereoacuity Test for patients with a history of anomalous binocular vision.

Distance is a significant influencing factor in the results of stereoacuity in patients with intermittent exotropia who have worsened stereoacuity with increased distance (6,7). However, in the healthy population, whether the distance significantly affects the stereopsis results (8) or has no effect on stereoacuity measurement (9) is not clear. Using the same test distance, the correlation between different stereopsis tests methods is poor (10).

The inconsistency between stereoacuity testing is due to numerous factors (11). These include the following: (I) the method of checking; i.e., using binoculars or an instrument to dissociate the two eyes (e.g., Frisby stereotest assesses in real depth without lenses, Titmus circle test assesses with polarized lenses, TNO assesses with anaglyph lenses). (II) The difficulty in performing the examination; i.e., in the Frisby stereotest the participant must determine whether the square containing a circle is protruding or sunken compared with the plane, while in the TNO test the participant must determine the depth and also identify the unfilled segment of the circle. (III) The size, shape, or density of the background in the stereo testing; in the case of the Frisby test, the random elements are widely spaced triangles, while in the TNO test, random dots are closely arranged and small. (IV) Monocular clues; the contour-based test may include monocular clues which can overestimate the threshold of stereopsis, while the random dot-based one does not contain monocular clues.

In order to address the element effect and to develop an objective evaluation of stereoacuity tests using contour-based and random dot-based graphs at far and near distance, we used two stereoacuity measurement systems which included laptop equipment 3D shutter glasses technology to test distance stereoacuity (12) and two 4K smartphones to test near stereoacuity (13), while contour-based and random-dot based pictures were designed side by side in a single graph.

Methods

Subjects

Thirty participants, 11 males and 19 females, were recruited with ages ranging between 20–31 years. In all participants, the visual acuity of each eye was not less than 0 logMAR, and the stereoacuity was not less than 40 second of arc (arcsec, ").

All participants gave their informed written consent before taking part in the study. The research protocol observed the tenets of the Declaration of Helsinki and was approved by the ethics committee of the Second Hospital of Jilin University (No. 2017-89).

Test system

Far distance test system

Equipment

A similar set up was used to that previously reported (12). The experiment used a 3D laptop (ASUS G750Y47JX, ASUSTEK Computer Inc., Taiwan) equipped with a NVidia 3D Vision 2 Wireless Glasses Kit (Expressway Santa Clara, CA, USA). NVidia 3D Vision Photo Viewer was used to display 3D images (Figure 1). A program was written using C# to generate all random-dot stereograms. Crossed disparity was used in all test graphs.

Figure 1 Legend of far distance stereopsis test system. (A) is seen by the left eye and (B) is seen by the right eye, the disparity of the stereo targets were 80". (C) is a simulation of the perception generated by the test images (A and B). The stereo symbol in random-dot graphs was in the upward direction, while the stereo symbol in contour-based graphs is to the left. (D) is a photograph of the test system.

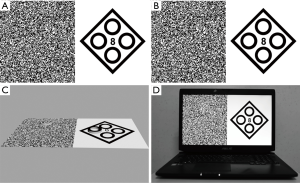
Test symbols

A test page containing two adjoining sections, which were a contour-based graph and random-dot graph was developed (Figure 1). For the contour-based symbol, the test symbol of the Fly Stereo Acuity test (Vision Assessment Corporation, Elk Grove Village, IL, USA) was used: a square with four circles. A stereo circle was hidden randomly which could be seen if the stereoacuity of the participant was better than the disparity of the specific stereo target. For the random-dot symbol, a solid circle of the same size with the circle of the contour-based symbol was designed, and each graph contained one circle in a random position of up, down, left, or right. A protruding image was identified if the threshold of the participant’s stereopsis was lower than the design disparities. Eight test pages were designed to test stereoacuity, ranging from 8-pixel to 1-pixel, which represented 80" to 10", respectively, at a 4.1 m test distance. On each test page, the contour-based symbol and random-dot symbol contained the same disparities.

Test procedure

The distance used for testing was 4.1 m, and the test page was 80" (Figure 1). The participants were required to identify the protruding circle in the contour-based graph and the protruding solid circle in the random-dot graph. If the participants identified them correctly, the test page was reduced to 70", etc., until the participant could not find the stereo target and the previous disparity was recoded as the stereopsis threshold of that participant. For example, if the participant could identify a 3-pixel disparity stereo target but failed to identify a 2-pixel disparity target in a random-dot graph, and could identify a 2-pixel disparity stereo target but failed to identify the 1-pixel disparity target in a contour-based graph, the stereoacuity of the participant was recoded as 30" in the random-dot test and 20" in the contour-based one.

Near distance test system

Equipment

A stereopsis measurement system using a phoropter (Topcon VT-10, Topcon Corp, Tokyo, Japan) and two Sony smartphones (Sony Xperia Z5 Premium Dual E6883; resolution, 3,840×2,160; Sony Mobile Communications Inc., Tokyo, Japan) (13) was developed. With the aid of two 5.5Δ base out (BO) Risley prisms, the participant could merge the two smartphone images into one image at a distance of 65 cm (Figure 2).

Figure 2 Legend of near distance stereopsis test system. (A) is seen by the left eye and (B) is seen by the right eye. From top to bottom, the disparity of the stereo targets was 40", 30", 20", and 10", respectively. From top to the end, the stereo symbol in the contour-based graphs were left, right, down, and up, respectively, while the stereo symbol in the random-dot graphs were down, up, right, and left, respectively. (C) is the simulation of the perception generated by the test images (A and B). The stereo symbols appeared to “pop out” of the background plane. (D) is a photograph of the test system.

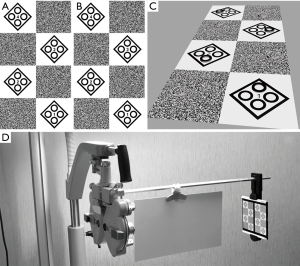
Test symbols

The test symbol design was similar to that of the far distance test system. The test page was simplified into two pages. Page one included 8-pixel, 7-pixel, 6-pixel and 5-pixel, while page two included 4-pixel, 3-pixel, 2-pixel and 1-pixel (Figure 2). One-pixel disparity represented 10" at a distance of 65 cm.

Test procedure

The distance used was 65 cm, and a first test page including 80" to 50" was used. The participant was required to identify the protruding circle in the contour-based graph and the protruding solid circle in the random-dot graph side by side from top to bottom. The resulting judgment was the same as for the far distance test system.

Statistics

All data was processed using MedCalc Statistical Software (version 17.6, MedCalc Software bvba, Ostend, Belgium). The Wilcoxon signed-rank test was used to test the difference between the groups. Stereoacuity values were transformed to log arcsec for analysis (14). The Bland-Altman method was used to test agreement between the two tests.

Results

The test results are shown in Figure 3. No significant differences were found between the results for contour-based and random-dot graphs at far distance (Wilcoxon signed-rank test: Z=–0.577, P=0.564) or at near distance (Wilcoxon signed ranks test: Z=–0.471, P=0.637). Similarly, no significant difference between far and near distance were found for the contour-based graphs (Wilcoxon signed-rank test: Z=–0.905, P=0.366) or random-dot graphs (Wilcoxon signed ranks test: Z=–0.333, P=0.739).

Figure 3 Boxplot of the stereoacuity of the four groups. The line perpendicular to the whisker below the box represents the minimum value; the lower edge of the box represents the first quartile; the line in the box is the median; the upper edge of the box represents the third quartile; and the line perpendicular to the whisker above the box represents the maximum value. The stars and circles represent extreme values.

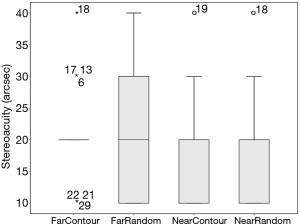
The mean stereoacuity measured using contour-based graphs at a far distance, random-dot graphs at a far distance, contour-based graphs at a near distance and random-dot graphs at a near distance were 1.30±0.16, 1.30±0.21, 1.30±0.18, and 1.30±0.18 log arcsec, respectively. The agreement between the contour-based graphs and the random-dot graphs at far distance were such that the 95% limits of agreement (LoA) were −0.25 to 0.32 log arcsec, and the maximum allowed difference between the methods [the interval between the lower 95% confidence interval (CI) limit of the lower LoA and the upper 95% CI limit of the higher LoA 95% CI] was −0.35 to 0.42 log arcsec (Figure 4A). The agreement between the contour-based graphs and the random-dot graphs at a near distance were such that the 95% LoA was −0.39 to 0.36 log arcsec, and the maximum allowed difference between the methods was −0.51 to 0.48 log arcsec (Figure 4B). The agreement of the contour-based graphs between far and near distances were such that the 95% LoA was −0.27 to 0.33 log arcsec, and the maximum allowed difference between the methods was −0.37 to 0.44 log arcsec (Figure 4C). The agreement of the random-dot graphs between far and near distances was such that the 95% LoA was −0.29 to 0.25 log arcsec, and the maximum allowed difference between methods was −0.38 to 0.34 log arcsec (Figure 4D).

Figure 4 Bland-Altman plots. (A) Comparison between the contour-based graphs and the random-dot graphs at far distance. Mean difference between methods was 0.034 log arcsec, and 95% confidence interval (CI) of the mean was −0.020 to 0.089 log arcsec. The 95% limit of agreement (LoA) was −0.25 to 0.32 log arcsec; the 95% CI limit of the lower LoA was −0.35 to −0.16 log arcsec; the 95% CI limit of the higher LoA was 0.23 to 0.42 log arcsec. (B) Comparison between the contour-based graphs and the random-dot graphs at near distance. Mean difference between methods was 0.016 log arcsec, and 95% CI of the mean was −0.087 to 0.055 log arcsec. The 95% LoA was −0.39 to 0.36 log arcsec; the 95% CI limit of the lower LoA was −0.51 to −0.27 log arcsec; the 95% CI limit of the higher LoA was 0.24 to 0.48 log arcsec. (C) Comparison the contour-based graphs between far and near distance. Mean difference between methods was 0.030 log arcsec, and 95% CI of the mean was −0.028 to 0.088 log arcsec. The 95% LoA was −0.27 to 0.33 log arcsec; the 95% CI limit of the lower LoA was −0.37 to −0.17 log arcsec; the 95% CI limit of the higher LoA was 0.23 to 0.44 log arcsec. (D) Comparison the random-dot graph between far and near distance. Mean difference between methods was −0.020 log arcsec, and 95% CI of the mean was −0.071 to 0.031 log arcsec. The 95% LoA was −0.29 to 0.25 log arcsec; the 95% CI limit of the lower LoA was −0.38 to −0.20 log arcsec; the 95% CI limit of the higher LoA was 0.16 to 0.34 log arcsec.

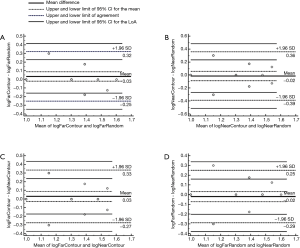
The 95% LoA of the contour-based graphs and the random-dot graphs at far distance, the contour-based graphs and the random-dot graphs at near distance, the contour-based graphs between far and near distance, and the random-dot graphs between far and near distance was ±0.29 log arcsec, ±0.38 log arcsec, ±0.30 log arcsec, and ±0.27 log arcsec, respectively, while the maximum allowed difference between methods was ±0.38 log arcsec, ±0.50 log arcsec, ±0.40 log arcsec, and ±0.36 log arcsec, respectively. However, ±5 arcsec (equivalent to ±0.7 log arcsec) was small enough for routine stereopsis testing in the clinic. The range of values was larger than any of the maximum difference allowed between methods in this study, indicating a high level of agreement.

Discussion

The disparity between stereopsis results using different methods could be due to the measurements used. Numerous evaluation methods have been proposed to detect minimal disparity. Some are performed under real circumstances, such as the Howard-Dolman apparatus and Frisby stereotest, and others require a tool to separate the image from each eye to see the test picture containing a certain disparity, such as the Titmus circle test using polarized glasses and the TNO test using red-green glasses. The number of disparities existing in the test system is the key to stereopsis testing. The threshold of the smallest disparity is the purpose of all testing.

Contour-based graphs and random dot based graphs are two different types of testing which hide disparities. The form in contour-based graphs is easy to distinguish, but monocular cues may cause an overestimation of the stereoacuity or even show a false positive (3). Random dot-based graphs could eliminate the interference of monocular cues, and give a relatively correct result. However, in clinical practice, inconsistencies occur between different tests (10). The difference may be caused by a different design and range used for each test; e.g., the test range of the Frisby test is from 20 arcsec to 600 arcsec (or stereonegative) and the range of the FD2 test is from 5 arcsec to 50 (or stereonegative) (15). The test step range is also different; e.g., at a 40 cm distance, the Frisby near stereotest (Sheffield, UK) may check 340" (6 mm plate thickness), 170" (3 mm plate thickness), and 85" (1.5 mm plate thickness), while the Fly Stereo Acuity Test (Vision Assessment Corporation, Elk Grove Village, IL, USA) can provide 400", 200", 160", 100", 63", 50", 40", 32", 25", and 20" test values. The ceiling is different; e.g., the value is 60" for TNO (version 19), while it is 40" for the Titmus Stereo Fly Test (Stereo Optical Co., Chicago, IL, USA).

The literature suggests that the TNO stereotest overestimates the stereo threshold compared to other clinical stereotests (3,16,17). The test results from the TNO stereotest, Randot circles (Stereo Optical, Inc., Chicago, USA), and 3D-assisted computer global and local psychophysical stereotests, have been compared, and the reported results agree that the TNO produces significantly higher estimates of the stereo threshold, while no difference in stereo threshold estimates were found between the other three stereotests (3). A threshold stereoacuity was reported for the Frisby, TNO, Randot circles, and Titmus circles tests, with the TNO test having the least similarity with the other three tests (16). Although the reason for this is not known, proposals have been made. One possible factor is the dot size (3), which is small with the density of the dots being high. The identification of random dots may increase as distinguishing them becomes more difficult, thus affecting a participants’ judgment. Another possible reason may be that it is difficult to identify the stereo symbols. The stereo target is a disk with a section missing. Unlike other routine tests that consist of simple circles or squares which are easily recognized, the “Pacman” appearing in TNO should be reported to look different and have a missing part. However, greater discrimination may increase the test difficulty. The method used to dissociate the two eyes may also be a factor resulting in a lower test result. Red-green glasses are required to conduct the experiment. Unlike polarized glasses which decrease the observation luminance, anaglyph glasses generate illumination imbalance and chromatic imbalance (17) which could create higher thresholds of the TNO stereo test.

The random dot graphs in this study were designed as follows: the size of the random dots were 6-pixel (6×6 pixels, covering a visual angle of 1 min; requiring an acuity of 0 logMAR to resolve at test distance), which could be observed clearly for participants with visual acuity 0 logMAR or greater. The stereo symbol was designed as a solid circle, and the participant was required to identify the side on which the circle appeared and did not need to distinguish any detail of the circle, reducing the difficulty of identification. Methods to dissociate binocular in the experiment balanced the images transmitted to both eyes. 3D liquid shuttle glasses used in the far distance test system reduced the light slightly in both eyes, and the image quality of the two eyes became the same. Two 5.5Δ BO prisms used in the near distance system also had little effect on the images of both eyes, unlike the anaglyph glasses used in the TNO which interfered with the image quality significantly.

In order to make a balance effect to compare the results of contour-based and random dot based graphs, a test picture was designed as follows: the contour-based and random-dot based graphs appeared in the same frame, so the participant could see the two stereo pictures simultaneously. The size and shape of the test symbol were the same. The position of the stereo target randomly appeared on the top, bottom, left, and right part of the picture, requiring the participant to identify the target at the same degree of difficulty. The test results for both the contour-based and random-dot based graphs were the same regardless of the distance across the cohorts.

The issue of far and near distance stereoacuity was investigated further in patients with binocular disorders. The literature reports that patients with intermittent exotropia demonstrated poor close stereoacuity when compared with healthy subjects, both preoperatively (P<0.001) and at six months postoperatively (P=0.004) (18). For normal cohorts, there is some controversy. Yildirim et al. (8) compared stereopsis between a near (Titmus, Randot circles, and TNO) and far distance stereopsis [Mentor B-VAT II-SG computerized testing system, which can test both contour (BVC) and global distance stereoacuity (BVRDE)], and found no significant mean difference between the Titmus and BVC tests (P>0.05); however, no correlation existed between the tests in each group (P>0.05). This discrepancy may have been be caused by the different measurement intervals and range of the tests, or could imply that distance and near stereo tests are possibly measuring different aspects of binocular vision. Wong’s study (9) reported different results, the distance-habitual and near-habitual BVRDE stereoacuities were not significantly different (Wilcoxon signed-rank test, Z=0.78, P=0.43) and distance-habitual and near-habitual BVC stereoacuities were not significantly different (Wilcoxon signed-rank test, Z=0.27, P=0.79) under normal viewing conditions. The results in this study are in agreement with those reported in the Wong study. In a normal population, the stereopsis is affected by binocular disparity, but cannot be affected by accommodation, convergence, or cognitive factors (9).

The limitation of this study was that the stereoacuity measured was not linear but existed in steps, which might have created a measurement error for a participant who had extremely good stereopsis. The ceiling effect existed, although 10" is good for healthy people but not sufficient for people with excellent stereopsis. The research was undertaken on young adults with normal stereopsis, and no difference was found between contour-based and random dot-based graphs at far and near distances. The results could vary if using different cohorts, such as young children, the elderly, or people with binocular disorders. Further study needs to be undertaken on these other cohorts to understand the differences across the population.

Conclusions

In a population with normal stereopsis, the stereoacuity was stable regardless of the test graph (contour-based or random-dot based) or the test distance (far or near). The stereopsis was affected only by binocular disparity.

Acknowledgements

Funding: This study was supported by a grant from the Jilin Provincial Science & Technology Department, China (No. 20170519004JH, No. 20190303150SF).

Footnote

Conflicts of Interest: The authors have no conflicts of interest to declare.

Ethical Statement: The study was approved by the ethics committee of the Second Hospital of Jilin University (No. 2017-89) and written informed consent was obtained from all patients.

References

1. Howard IP, Rogers BJ. Stereoscopic acuity. In: Howard IP, Rogers BJ. editors. Perceiving in Depth. New York: Oxford University Press, 2012:287-362.
2. Fawcett SL, Birch EE. Validity of the Titmus and Randot circles tasks in children with known binocular vision disorders. J AAPOS 2003;7:333-8. [Crossref] [PubMed]
3. Vancleef K, Read JCA, Herbert W, et al. Overestimation of stereo thresholds by the TNO stereotest is not due to global stereopsis. Ophthalmic Physiol Opt 2017;37:507-20. [Crossref] [PubMed]
4. Pai AS, Rose KA, Samarawickrama C, et al. Testability of refraction, stereopsis, and other ocular measures in preschool children: the Sydney Paediatric Eye Disease Study. J AAPOS 2012;16:185-92. [Crossref] [PubMed]
5. Fawcett SL. An evaluation of the agreement between contour-based circles and random dot-based near stereoacuity tests. J AAPOS 2005;9:572-8. [Crossref] [PubMed]
6. Stathacopoulos RA, Rosenbaum AL, Zanoni D, et al. Distance stereoacuity: Assessing control in intermittent exotropia. Ophthalmology 1993;100:495-500. [Crossref] [PubMed]
7. Seki Y, Wakayama A, Takahashi R, et al. Influence of Test Distance on Stereoacuity in Intermittent Exotropia. Strabismus 2017;25:12-6. [Crossref] [PubMed]
8. Yildirim C, Altinsoy HI, Yakut E. Distance stereoacuity norms for the mentor B-VAT II-SG video acuity tester in young children and young adults. J AAPOS 1998;2:26-32. [Crossref] [PubMed]
9. Wong BP, Woods RL, Peli E. Stereoacuity at distance and near. Optom Vis Sci 2002;79:771-8. [Crossref] [PubMed]
10. Hall C. The relationship between clinical stereotests. Ophthalmic Physiol Opt 1982;2:135-43. [Crossref] [PubMed]
11. Simons K. Stereoacuity norms in young children. Arch Ophthalmol 1981;99:439-45. [Crossref] [PubMed]
12. Wu H, Jin H, Sun Y, et al. Evaluating stereoacuity with 3D shutter glasses technology. BMC Ophthalmol 2016;16:45. [Crossref] [PubMed]
13. Wu H, Liu S, Wang R. Stereoacuity measurement using a phoropter combined with two 4K smartphones. Clin Exp Optom 2018;101:272-5. [Crossref] [PubMed]
14. Ma DJ, Yang HK, Hwang JM. Reliability and validity of an automated computerized visual acuity and stereoacuity test in children using an interactive video game. Am J Ophthalmol 2013;156:195-201.e1. [Crossref] [PubMed]
15. Bohr I, Read JC. Stereoacuity with Frisby and revised FD2 stereo tests. PLoS One 2013;8:e82999. [Crossref] [PubMed]
16. Antona B, Barrio A, Sanchez I, et al. Intraexaminer repeatability and agreement in stereoacuity measurements made in young adults. Int J Ophthalmol 2015;8:374-81. [PubMed]
17. Cornforth LL, Johnson BL, Kohl P, et al. Chromatic imbalance due to commonly used red-green filters reduces accuracy of stereoscopic depth perception. Am J Optom Physiol Opt 1987;64:842-5. [Crossref] [PubMed]
18. Sharma P, Saxena R, Narvekar M, et al. Evaluation of distance and near stereoacuity and fusional vergence in intermittent exotropia. Indian J Ophthalmol 2008;56:121-5. [Crossref] [PubMed]