Overview of clinical prediction models

Clinical prediction models are becoming more and more popular over recent years, which could be used in not only medicine area but also other areas, such as engineering, mathematics, and computer science (1). In 2015, Collins et al. proposed a reporting guideline for clinical prediction models—TRIPOD (Transparent reporting of a multivariable prediction model for individual prognosis or diagnosis), which was simultaneously published in 11 leading journals (Ann Intern Med, Br J Cancer, Circulation, BMJ, J Clin Epidemiol, Eur Urol, BMC Med, Eur J Clin Invest, Br J Surg, BJOG and Diabet Med) and cited thousands of times until now. But TRIPOD did not talk much about the modelling details. Steyerberg updated his classic book—Clinical Prediction Models: A Practical Approach to Development, Validation, and Updating in 2019, which is an invaluable resource to help us comprehensively master this area (1). Regression modelling strategies by Harrell discussed more technical details about linear models, logistic and ordinal regression, and survival analysis, which could help us deeply understand this area (2). Both are excellent resources to help us systematically learn this area. However, reading and understanding them needs a lot of time (The length of the former is 558 papers and the latter is 582 pages), which is not so feasible for busy clinicians who wish to perform clinical prediction models for specific clinical questions and have difficult to find an appropriate biostatistician to collaborate. Zhou et al. (3) wrote a series of methodologic papers which focused on commonly used methods and provided relevant R codes.

The use of clinical prediction models

Steyerberg defined public health, clinical practice, and medical research were three main application branches for clinical prediction models (1). For public health branch, to predict the future occurrence of disease is one main purpose, which could be used for targeting of preventive intervention (1). For example, we could use Framingham risk functions to classify the patients, and then prescribe statin for those with high risk to develop cardiovascular diseases. For clinical practice branch (1), we have several options: (I) decide whether we need further testing by predicting the probability of the underlying disease. We could give the invasive and costly gold standard test to the patients with high risk of the developing the disease to reduce the unnecessary harm; (II) decide whether we need to start a treatment/use more intensive treatment/perform a cost-effectiveness of a treatment/delay a treatment through decision analysis. We will start a treatment after diagnostic workup if the probability of the diagnosis is higher than the treatment threshold (the probability where the expected benefit of treatment is equal to the expected benefit of avoiding treatment); (III) decide whether we need a surgery by balancing short-term risks (e.g., 30-day mortality) and long-term risks (e.g., long-term survival and fracture risk). For medical research branch (1), we have two main options: (I) randomized controlled trials: select appropriate participants and covariate adjustment. (II) Observational studies: for confounder adjustment and case-mix adjustment.

Description of clinical prediction models

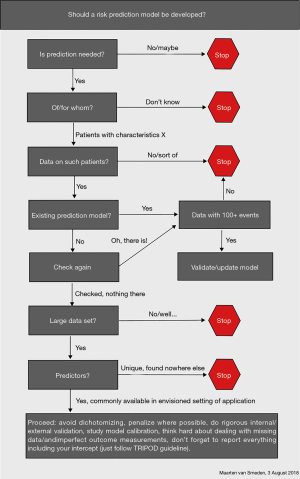
To develop valid prediction models, Steyerberg (1) proposed a checklist which includes three domains: general considerations, 7 modelling steps and validity. For domain general considerations, research question, intended application, outcome, predictors, study design, statistical model and sample size should be considered. For domain 7 modelling steps, the first step is preliminary, the second is coding of predictors, the third is model specification, the fourth is model estimation, the fifth is model performance, the sixth is model validation and the seventh is model presentation. For domain validity, interval: overfitting and external: generalizability should be considered. Bonnett et al. (4) developed a guide for presenting clinical prediction models. Points score system, graphical score chart, nomogram, and websites and applications are four main presentation formats. But they all have advantages and disadvantages. The researchers should consider who are the end users, when and in what setting they will use the models, and then choose a suitable format to present. The flowchart (Figure 1) from van Smeden (5) is another resource to guide our thinking of developing the models. In many situations, we may not need to develop a model because there are many models already developed for a large variety of conditions.

Figure 1 Should a risk prediction model be developed?

How was the clinical prediction model introduced in this study

This study includes a series of methodologic papers about clinical prediction model, Zhou et al. (3) uses 16 sections to carefully describe commonly used methods with detailed R codes. In section one, the authors introduced the theory foundation and application status of clinical prediction model. In section two, the authors introduced the methods about predictor selection. From section three to six, the authors described two widely used statistical models (logistic regression model and Cox proportional hazard model) as well as their nomogram drawing and c-index calculation. From section seven to eight, the authors described two indexes which could be used to evaluate the improvement in prediction performance—Net Reclassification Index (NRI) and Integrated Discrimination Index (IDI). From section nine to ten, the authors discussed decision curve analysis and its application in survival outcome data. From section 11 to 12, the authors supplementally introduced validation knowledge in both logistic regression and Cox regression. From section 13 to 14, the authors introduced competing risk model as well as its nomogram drawing. In section 15, the authors introduced the strategies to handle outliers and missing values. In section 16, the authors introduced several advanced topics (e.g., ridge regression and LASSO regression) which is becoming more and more popular in the area of variable selection and penalized estimation.

Limitations in this study

Some of the principles Zhou et al. (3) mentioned in this study are old-fashioned, and we should be cautiously in these areas. For continuous variable, Zhou et al. (3) mentioned that we should transform it into dichotomous or ordinal categorical variable if the relationship between the variable and the outcome is nonlinear. Based on PROBAST (Prediction model Risk of Bias Assessment Tool) (6), dichotomization or categorization of the continuous predictors would lose information. The exception is that the cut points are widely accepted rather than based on the data. We should consider using restricted cubic splines or fractional polynomials for the nonlinear relation. For variable screening method, Zhou et al. (3) mentioned that we should simultaneously consider the results from univariate analysis, clinical reasons, sample size and statistical power. Based on PROBAST (6), we should avoid using univariable analysis in predictors selection because some predictors are important only after adjustment for other predictors and some accidental associations exist. We need to consider: (I) existing knowledge of previously established predictors; (II) the reliability, consistency, applicability, availability, and costs of predictor measurement relevant to the targeted setting; (III) statistical methods which do not based on test results between predictor and outcome could be used as one way to reduce the number of the predictors.

Recent advances

Data source

Single-center retrospective cohort study and registry database were commonly used in clinical prediction models because they were relatively cheap and easy to obtain (1). But they also have some limitations, such as missing data issue and inappropriate definition/assessment of predictors/outcomes (1). Carefully designing the study, and then prospective collecting the data should be the ideal way except it is too expensive and time-consuming (7). Pajouheshnia et al. (8) proposed that we might consider using the data from existing randomised clinical trials (RCTs) to reduce potential research waste. But we should be cautiously because seven issues might threaten the viability of RCT data use: consent, selective inclusion of centres, selective eligibility and enrolment, predictor measurement, extraneous trial effects, short term and surrogate outcomes, and sample size (8). The detailed strategies to handle these issues could be found in their paper (8).

Sample size

The minimum number of events per predictor parameter (EPP) was proposed to decide whether the sample size is enough. Previously, we always used the rule of the thumb as a criterion, such as 10 EPP (9). Two simulation studies by van Smeden et al. (10,11) indicated that 10 EPP was not valid. Then, Riley et al. (12,13) proposed a new system: for continuous outcomes, firstly, small optimism in predictor effect estimates as defined by a global shrinkage factor of ≥0.9, secondly, small absolute difference of ≤0.05 in the apparent and adjusted R², thirdly, precise estimation (a margin of error ≤10% of the true value) of the model’s residual standard deviation, fourthly, precise estimation of the mean predicted outcome value (model intercept); for binary and time-to-event outcomes, the first rule is the same with the continuous outcome, the second rule is small absolute difference of ≤0.05 in the model's apparent and adjusted Nagelkerke’s R², the third rule is precise estimation of the overall risk in the population.

Risk of bias assessment tool

We normally classified prediction research into predictor finding studies, prediction model studies and prediction model impact studies (14). Hayden et al. developed QUIPS (Quality In Prognosis Studies) tool to assess risk of bias (ROB) in predictor finding studies (15). ROB 2.0 (revised ROB assessment Tool) and ROBINS-I (Risk Of Bias In Nonrandomized Studies of Interventions) could be used to assess ROB in prediction model impact studies through RCT design and nonrandomized design, respectively (16,17). Wolff et al. developed PROBAST to assess ROB in prediction model studies (6). This tool includes four domains (participants, predictors, outcome, and analysis) and 20 signalling questions, which could comprehensively assess the all steps (develop, validate, or update) for prediction model studies.

Uncertainly with using clinical prediction model

Discrimination and calibration are two commonly used ways to assess the usefulness of clinical prediction models (18). But these two indexes might not guarantee the robustness of the absolute risk from the model. Pate et al. (19) performed an uncertainty analysis (20), a tool to assess whether the models work well in individuals, through six different modelling strategies (model A to model F) for cardiovascular risk prediction from UK data. Although the Harrell’s c-index is very similar among different models (female: 0.86–0.87; male: 0.84–0.85), the absolute risk varied under different modelling strategies (e.g., for female cohort, if the 10-year risk using model A is 9–10%, model B is 8–13.5%, model C is 7.7–16.1%, model D is 4.9–15%, model E is 4.6–15.5% and model F is 4.4–16.3%). How to choose covariates, the secular trend, geographical location and how to handle missing data considerably affect the results (19).

Machine learning issue

The term machine learning (ML) is extremely hot nowadays, and a number of clinical prediction model studies used this sort of technologies. But there is no clear line between ML technologies and traditional statistical methods. Van Calster et al. (21) indicated that these two systems lie on a continuum (from less to more flexible, and from more data reliance less subject knowledge to less data reliance more subject knowledge. In their systematic review and meta-analysis (ML versus logistic regression, LP) (22), LP was defined as standard maximum likelihood plus penalized logistic regression (lasso, ridge, elastic net). Other traditional statistical methods, such as Poisson regression, generalized estimating equations and generalized additive models were excluded from ML technologies. They found that ML did not work better over LR using the receiver operating characteristic curve (AUC) as a criterion. We might need to prepare the analysis plan more carefully when we want to use some fancy models in the clinical prediction model studies. Collins et al. are developing a new reporting guideline for artificial intelligence prediction models (23), which will provide a standard for this relatively messy area.

Further reading

Besides all the references cited, there are still many good resources. I listed some of them for readers’ consideration:

• Riley RD, van der Windt D, Croft P, Moons KG. (Eds.). (2019). Prognosis Research in Healthcare: Concepts, Methods, and Impact. Oxford University Press.
• Wickham H, Grolemund G. (2016). R for data science: import, tidy, transform, visualize, and model data. "O'Reilly Media, Inc.".
• Decision Curve Analysis: https://www.mskcc.org/departments/epidemiology-biostatistics/biostatistics/decision-curve-analysis

Acknowledgments

The author thanks Dr. Maarten van Smeden for his insightful technical suggestions to considerably improve the quality of the paper.

Footnote

Conflicts of Interest: The author has no conflicts of interest to declare.

Ethical Statement: The author is accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.

References

1. Ewout WS. Clinical Prediction Models: A Practical Approach to Development, Validation, and Updating. SPRINGER NATURE; 2019.
2. Harrell FE Jr. Regression modeling strategies: with applications to linear models, logistic and ordinal regression, and survival analysis. Springer; 2015.
3. Zhou ZR, Wang WW, Li Y, et al. In-depth mining of clinical data: the construction of clinical prediction model with R. Ann Transl Med 2019;7:796. [Crossref] [PubMed]
4. Bonnett LJ, Snell KIE, Collins GS, et al. Guide to presenting clinical prediction models for use in clinical settings. BMJ 2019;365:l737. [Crossref] [PubMed]
5. van Smeden M. Should a risk prediction model be developed?. 2018. Available online: https://twitter.com/MaartenvSmeden/status/1025315100796899328. Accessed 2 November 2019.
6. Wolff RF, Moons KGM, Riley RD, et al. PROBAST: A Tool to Assess the Risk of Bias and Applicability of Prediction Model Studies. Ann Intern Med 2019;170:51-8. [Crossref] [PubMed]
7. Moons KG, Royston P, Vergouwe Y, et al. Prognosis and prognostic research: what, why, and how? BMJ 2009;338:b375. [Crossref] [PubMed]
8. Pajouheshnia R, Groenwold RH, Peelen LM, et al. When and how to use data from randomised trials to develop or validate prognostic models. BMJ 2019;365:l2154. [Crossref] [PubMed]
9. Peduzzi P, Concato J, Kemper E, et al. A simulation study of the number of events per variable in logistic regression analysis. J Clin Epidemiol 1996;49:1373-9. [Crossref] [PubMed]
10. van Smeden M, Moons KG, de Groot JA, et al. Sample size for binary logistic prediction models: Beyond events per variable criteria. Stat Methods Med Res 2019;28:2455-74. [Crossref] [PubMed]
11. van Smeden M, de Groot JA, Moons KG, et al. No rationale for 1 variable per 10 events criterion for binary logistic regression analysis. BMC Med Res Methodol 2016;16:163. [Crossref] [PubMed]
12. Riley RD, Snell KI, Ensor J, et al. Minimum sample size for developing a multivariable prediction model: PART II - binary and time-to-event outcomes. Stat Med 2019;38:1276-96. [Crossref] [PubMed]
13. Riley RD, Snell KIE, Ensor J, et al. Minimum sample size for developing a multivariable prediction model: Part I - Continuous outcomes. Stat Med 2019;38:1262-75. [Crossref] [PubMed]
14. Hemingway H, Croft P, Perel P, et al. Prognosis research strategy (PROGRESS) 1: A framework for researching clinical outcomes. BMJ: British Medical Journal 2013;346:e5595. [Crossref] [PubMed]
15. Hayden JA, van der Windt DA, Cartwright JL, et al. Assessing bias in studies of prognostic factors. Ann Intern Med 2013;158:280-6. [Crossref] [PubMed]
16. Sterne JA, Hernán MA, Reeves BC, et al. ROBINS-I: a tool for assessing risk of bias in non-randomised studies of interventions. BMJ 2016;355:i4919. [Crossref] [PubMed]
17. Sterne JAC, Savović J, Page MJ, et al. RoB 2: a revised tool for assessing risk of bias in randomised trials. BMJ 2019;366:l4898. [Crossref] [PubMed]
18. Alba AC, Agoritsas T, Walsh M, et al. Discrimination and Calibration of Clinical Prediction Models: Users’ Guides to the Medical Literature. JAMA 2017;318:1377-84. [Crossref] [PubMed]
19. Pate A, Emsley R, Ashcroft DM, et al. The uncertainty with using risk prediction models for individual decision making: an exemplar cohort study examining the prediction of cardiovascular disease in English primary care. BMC Med 2019;17:134. [Crossref] [PubMed]
20. Hofer E. The Uncertainty Analysis of Model Results: A Practical Guide. Springer; 2018.
21. Van Calster B, Verbakel JY, Christodoulou E, et al. Statistics versus machine learning: definitions are interesting (but understanding, methodology, and reporting are more important). J Clin Epidemiol 2019;116:137-8. [Crossref] [PubMed]
22. Christodoulou E, Ma J, Collins GS, et al. A systematic review shows no performance benefit of machine learning over logistic regression for clinical prediction models. J Clin Epidemiol 2019;110:12-22. [Crossref] [PubMed]
23. Collins GS, Moons KGM. Reporting of artificial intelligence prediction models. Lancet 2019;393:1577-9. [Crossref] [PubMed]