Aerosol bolus dispersion in healthy and asthmatic children—theoretical and experimental results
Original Article

Aerosol bolus dispersion in healthy and asthmatic children—theoretical and experimental results

Robert Sturm

Brunnleitenweg 41, A-5061 Elsbethen, Salzburg, Austria

Correspondence to: Dr. Robert Sturm. Brunnleitenweg 41, A-5061 Elsbethen, Salzburg, Austria. Email: sturm_rob@hotmail.com.

Introduction: In the past decades, aerosol bolus inhalation increasingly came into the focus of medical interest due to its potential as a non-invasive technique for the diagnosis of lung diseases. The experimental studies were accompanied by the development of theoretical contributions dealing with aerosol bolus behaviour in healthy and diseased lungs. In this study, bolus dispersion in healthy and asthmatic children is subject to a theoretical approach. Model predictions are validated with related experimental findings.

Methods: Aerosol bolus transport was simulated by using (I) a stochastic model of the human respiratory tract; (II) appropriate scaling procedures for the generation of healthy and asthmatic lungs of children; and (III) the concept of effective diffusivities (Deff) for the prediction of convective mixing processes in the conducting airways and alveoli. The aerosol injected into the inhalative air stream consisted of monodisperse particles with a diameter of 0.4 µm (ρ =1 g∙cm–3). Volumetric lung depth, being a measure for the position of the aerosol bolus within the inspired air stream, was varied from 95 mL (shallow bolus) to 540 mL (deep bolus). Half-width of the inhaled bolus was set to 50 mL.

Results: According to the predictions provided by the model, dispersion of the exhaled aerosol bolus increases exponentially with volumetric lung depth in both asthmatic children and healthy controls. Asthmatics tend to develop higher bolus dispersion than healthy subjects, with significant differences between the two groups being noticeable at low volumetric lung depths (<300 mL). Skewness decreases with increasing volumetric lung depth, whereby respective values calculated for asthmatics exceed those values computed for healthy subjects. Theoretical results correspond very well with experimental findings.

Discussion and conclusions: Results of experimental bolus studies may be approximated by theoretical models with high accuracy. Model predictions confirm the assumption that inhalation of aerosol boluses and dispersion measurements have only a limited diagnostic potential.

Keywords: Aerosol bolus; convective mixing; stochastic lung; effective diffusivity; asthma

Submitted Mar 10, 2014. Accepted for publication Apr 22, 2014.

doi: 10.3978/j.issn.2305-5839.2014.04.13

Introduction

Inhaled aerosol particles, ranging in size from 0.1 to 1.0 µm, are commonly characterized by minimal deposition forces, which depend on physical particle properties as well as geometrical and mechanical properties of a subject’s lungs. Therefore, in pneumological research these specific particles are mainly administered as tracers, which indicate intrapulmonary convective transport and mixing phenomena (1-6). For this purpose, a small volume (e.g., 20 cm3) of air is labelled with sub-micron test particles and inserted into a subject’s inspiratory volume, where it is transported into the lungs as an “aerosol bolus”. During their inhalative and exhalative passage through the air-conducting structures of the lungs, particles of the aerosol bolus are increasingly dispersed to adjacent air volumes due to convective and diffusive processes (1,2). As a result of this phenomenon, the expired aerosol bolus is spread over a larger air volume than the inspired aerosol bolus. This so-called aerosol bolus dispersion was found to exhibit a certain sensitiveness to any disease-induced changes of the lung architecture (7-16).

The potential for a meaningful application of aerosol bolus dispersion as a measure of pulmonary disease was shown for the first time by McCawley and Lippmann (7), who compared the aerosol bolus behaviour of smokers with that of age- and gender-matched nonsmokers. The authors could find that bolus dispersion was increased in the smokers with respect to the nonsmokers, whereas spirometric data were almost identical among the two test groups. Further scientific studies demonstrated that bolus dispersion is also enhanced in patients with other lung insufficiencies such as cystic fibrosis (8), chronic obstructive pulmonary disease (COPD) (9-11), emphysema (12-15) as well as chronic asthma (16). A comparable effect may be observed after acute exposure of healthy probands to 0.4 ppm ozone in combination with physical exercise (2,17). Most of the clinical investigations noted above came to the conclusion that aerosol bolus dispersion provides interesting information on certain modifications of convective gas transport in diseased lungs, but has only a limited potential for the clinical diagnosis of pulmonary insufficiencies. In numerous cases measurement of FEV1/FVC exhibits a comparable disease-specific sensitiveness, but causes much lower medical costs.

The main focus of the present study is set on the investigation of aerosol bolus behaviour in healthy and asthmatic children. In general, asthma represents a lung disease with airways narrowing readily and excessively in response to a high number of provoking stimuli (18). Analysis of this endogenous hyperresponsiveness of the tracheobronchial tree is useful for both the diagnosis of asthma and the determination of severity of disease. Since the 1960s, methacholine (MCh) or histamine has been administered as aerosolized drugs to asthmatic patients in order to provoke bronchoconstrictions (18-20). Measurement of the bronchial response has been conducted in different ways, including the analysis of airway resistance (Raw) with plethysmography and the study of aerosol bolus behaviour (18,21). The present contribution attends to approximate aerosol bolus dispersion in healthy and asthmatic children with the help of theoretical models which have run through numerous processes of improvement and validation (22-29). Theoretical computations were carried out on the basis of experimental investigations outlined by Schulz et al. (16). Simulations of aerosol bolus behaviour may support clinical diagnosis in several ways: first, they may help to optimize breathing conditions during bolus inhalation; second, the physical properties of aerosolized particles may be tested in order to minimize any side effects; and third, they may support or doubt clinical diagnosis based on experimental measurements.

Material and methods

Modeling aerosol bolus transport and dispersion

The aerosol bolus model used in this study has been already described in earlier contributions (25-28), so that, for the sake of brevity, only the most salient features of this approach are described here. Aerosol bolus dispersion may be regarded as result of convective gas mixing in the conductive airways, which is approximated by effective diffusivities (Deff) for inhalation and exhalation. These parameters are commonly expressed by the equations (26)

Deff = χ(D + 1.08ud) for inhalation [1]

and

Deff = χ(D + 0.37ud) for exhalation [2]

where χ denotes a correction factor for small particles, whereas D, u, and d represent the diffusion coefficient (cm2∙s–1) obtained from the Einstein-Stokes-equation, the mean velocity of the inhaled air stream in a given airway tube, and the cylindrical diameter of this airway, respectively. The time of an aerosol bolus to pass a given airway with the length L is obtained from a Gaussian probability distribution [P(t)] of the following form (22):

P(t) = 1/[Deff∙(2π)1/2]∙exp[-(L – u∙t)/(4Deff∙t)] [3]

For further use, this distribution is re-arranged to a so-called probability density function [D(t)], which takes the form:

D(t) = ∫ 1/[Deff∙(2π)1/2]∙exp[-(L – u∙t)/(4Deff∙t)]dt [4]

Transit time used for statistical computations is randomly selected from this function.

In the alveoli, mixing between inhaled and residual air represents the main contribution to aerosol bolus dispersion. In the model, ideal mixing between these air volumes may be distinguished from not mixing at all (27,28). Non-mixing is simulated by application of the so-called “first-in-last-out” concept: particles, which enter an alveolus at the very beginning of the inhalation period, leave that alveolus again at the very end of the breath-cycle. According to earlier contributions on this topic (27), the mathematical relation between ideal mixing and non-mixing may be expressed by an empirical mixing factor, which is committed to a value of 0.25 (i.e., 25% ideal mixing and 75% “first-in-last-out” approximation).

Bolus statistics based on normalized mathematical moments and including the computations of half-width, standard deviation, skewness, and mode-shift of the exhaled aerosol bolus were conducted according to a mathematical standard procedure, which is described in very detail in earlier studies (1-6,28).

Simulation of asthmatic lung architecture

Simulation of the basic lung architecture was conducted by using lung-generation-specific probability D(t) for the distributions of airway diameters, airway lengths, branching angles, and gravity angles (i.e., the angles of single airway tubes relative to the direction of gravity) (30). Geometric parameters of each lung airway were randomly selected from these probabilities D(t), using the random number concept. Necessary morphometric data were obtained from interferometric measurements of the tracheo-bronchial tree (31) and the acinar compartment of the human lung (32). Modeling resulted in the construction of random bronchial pathways and the junction of a pre-selected number of these paths (e.g., 10,000) to the stochastic lung.

Originally, the stochastic lung was standardized to a functional residual capacity (FRC) of 3,300 mL, representing the mean value for a male Caucasian adult (33). Size-reduced lung morphometry of younger individuals may be obtained by application of scaling factors (SF). According to Phalen et al. (34), the dimensions of the trachea and bronchi may be related to body height according to the simple mathematical equation

SF = a∙(Hs − 1.76) + 1 [5]

where SF denotes the ratio of airway diameter or length in the subject compared to that in reference man, whereas HS represents the height of the subject in meters and a an airway-generation-specific constant (33,34). Another possibility of lung scaling is given by the expression

SF = (FRCS/FRCR)1/3 [6]

with FRCS denoting the FRC of the subject of interest and FRCR being the FRC of a reference subject (33).

Asthmatic lungs were subjected to an additional re-calibration, which is based on the circumstance that airway obstructions result in an increase of Raw (Table 1). The related scaling algorithm was introduced by Segal et al. (35), who defined the following calibration factor:

Table 1
Table 1 Essential physiological factors of healthy and asthmatic children obtained from experimental studies (exp) (16). Airway resistances (Raw) were modeled using the algorithm of Segal et al. (35)
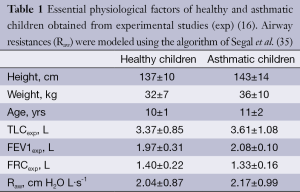
Full table

SF = [(Rlaw – Rp)/RTB]1/4 [7]

In Eq. [7], Rlaw denoted Raw in the lower (thoracic) airways, whereas Rp represents Raw in the pulmonary airways (lung generations 17 to 23) and RTB Raw in the tracheobronchial airways (lung generations 0 to 16). Rp and RTB are obtained from the equations

Rp = ∑i=17-23 2-i∙ri and RTB = ∑i=0-16 2-i∙ri [8]

where ri is the flow resistance in a given airway of generation i and may be computed according to the mathematical approximation of Pedley (36). Application of the re-calibration algorithm shows that airway calibers of mild asthmatics have to be reduced by another 10% to 20%.

Experimental measurements

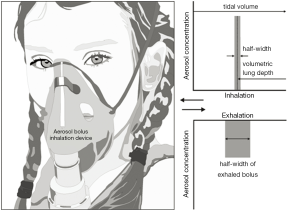
In the study provided by Schulz et al. (16) aerosol bolus measurements were performed with a group of 16 healthy children, serving as controls, and a group of 47 children suffering from mild asthma. Breathing manoeuvres for an effective inhalative uptake of the aerosol particles were standardized on the basis of FRC, expiratory reserve volume (ERV), and total lung capacity (TLC), which were measured in a constant volume plethysmograph. Inhalation tests were conducted with the help of an apparatus consisting of a pneumotachograph for the analysis of respiratory flows and a specific valve system with one expiratory and two inspiratory paths. The test aerosol contained di-(2-ethylhexyl) sebacate particles with a diameter of 0.4±0.1 µm. For the measurement of aerosol bolus dispersion, inhalative flow rate of the healthy and diseased probands was uniformly manifested with 300 cm2∙s-1, and tidal volume (TV) was allowed to reach from FRC to 80% TLC, corresponding to 1,500-1,750 cm3. The inspired aerosol bolus was set to 50 cm3 and was introduced into the filtered air 95, 140, 240, 340, 440, and 540 cm3 before the end of inhalation (= volumetric lung depth, VLD; Figure 1). Maximum duration of the aerosol measurements was committed to 30 min, but children were not tested anymore within this time span, if they refused to continue or felt exhausted from prior analyses.

Figure 1 Sketch illustrating main characteristics of the inhaled and exhaled aerosol bolus as well as the definition of the volumetric lung depth. The higher this factor is, the earlier is the bolus injected into the inspired air stream. Early injection of aerosol particles into the air stream results in a deep bolus, late injection in a shallow bolus.

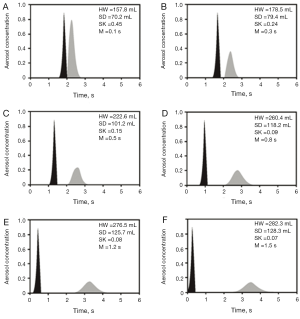
Results

As demonstrated by the theoretical model, aerosol bolus dispersion in asthmatic children differs from that in healthy controls (Figures 2,3). In healthy children, bolus half-width is increased from 157.8 mL at shallow boluses (VLD =95 mL) to 282.3 mL at deep boluses (VLD =540 mL), which corresponds to a 79.8% enhancement of this parameter. In asthmatic children the same parameter changes from 170.1 mL (VLD =95 mL) to 292.3 mL (VLD =540 mL) and thus processes an increase of 71.8%. Comparison of the results between the two groups shows that asthmatic children have higher half-widths of the exhaled boluses than healthy children, with significant discrepancies being noticeable for low values of VLD. A similar tendency may be observed for the standard deviation of the exhaled bolus, which is enhanced from 70.1 mL (VLD =95 mL) to 128.3 mL (VLD =540 mL) in healthy controls and from 77.3 mL (VLD =95 mL) to 149.5 mL (VLD =540 mL) in young asthmatic patients. The percentual increases, however, amount to 83.0% (healthy) and 93.4% (asthmatic). Again, significant differences may be only noticed for shallow boluses with VLD <300 mL. Skewness of the exhaled bolus, representing another essential parameter for bolus description, decreases from 0.45 (VLD =95 mL) to 0.07 (VLD =540 mL) in healthy controls. In asthmatic children this parameter is reduced from 0.44 (VLD =95 mL) to 0.14 (VLD =540 mL). Here, significant differences between both investigated groups mainly occur at high VLDs (>300 mL). The peak mode of the exhaled bolus is shifted from 0.1 s (VLD =95 mL) to 1.5 s (VLD =540 mL) in healthy children, but from 0.1 s (VLD =95 mL) to 1.7 s (VLD =540 mL) in children with asthma.

Figure 2 Behaviour of the inhaled aerosol bolus in the lungs of healthy controls: (A) VLD =95 mL; (B) VLD =140 mL; (C) VLD =240 mL; (D) VLD =340 mL; (E) VLD =440 mL; (F) VLD =540 mL. Abbreviations: HW, half-width of the exhaled bolus; SD, standard deviation of the exhaled bolus; SK, skewness of the exhaled bolus; M, mode-shift of the exhaled bolus.
Figure 3 Behaviour of the inhaled aerosol bolus in the lungs of asthmatic children: (A) VLD =95 mL; (B) VLD =140 mL; (C) VLD =240 mL; (D) VLD =340 mL; (E) VLD =440 mL; (F) VLD =540 mL. Abbreviations: HW, half-width of the exhaled bolus; SD, standard deviation of the exhaled bolus; SK, skewness of the exhaled bolus; M, mode-shift of the exhaled bolus.

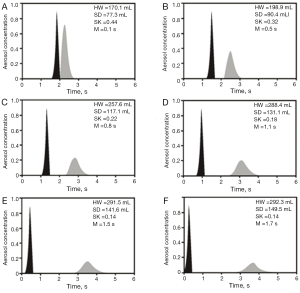
Comparisons between theoretical data and related experimental results outlined by Schulz et al. (16) are summarized in Figures 4 and 5. Concerning the standard deviation of the exhaled aerosol bolus, model predictions correspond well with experimental data for both healthy and asthmatic children, with highest discrepancies between the two data sets being on the order of 5%. Best predictive accuracy may be found for VLD >300 mL, whereas modeling of shallow bolus scenarios bears slightly higher uncertainties. With regards to the skewness of the exhaled aerosol bolus, most experimental measurements (mean values ± standard deviations) exhibit fair correspondence with related theoretical predictions. In healthy controls, differences between the two data sets may reach up to 20%, thereby becoming most significant for shallow boluses (VLD <300 mL). In asthmatic children, discrepancies between theoretical and experimental results reach a similar order of magnitude as in healthy controls, but are more significant for deeper boluses (VLD >300 mL).

Figure 4 Standard deviation (SD) of the exhaled aerosol bolus in healthy controls (A) and asthmatic children (B).
Figure 5 Skewness (SK) of the exhaled aerosol bolus in healthy controls (A) and asthmatic children (B).

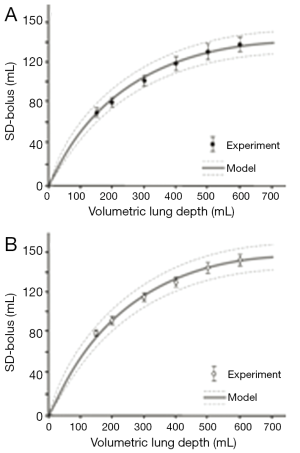
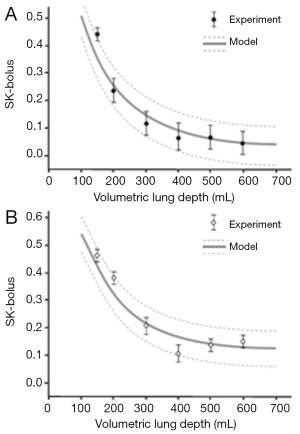
Discussion and conclusions

This contribution could demonstrate that the behaviour of aerosol boluses in healthy and asthmatic lungs of children may be approximated mathematically with high accuracy. This is mainly due to a continuous improvement and refinement of aerosol bolus models during the past 40 years (22-29). Most current publications on this topic were exclusively limited to adult lungs, so that this study has to be understood as further developmental stage in theoretical lung physics. As exhibited by the modeling results and confirmed by experimental measurements (16), aerosol bolus dispersion is altered in asthmatic children with respect to their healthy controls. This modification is primarily expressed by an increase in standard deviation and skewness of the exhaled aerosol boluses (Figures 4,5). From a theoretical point of view, axial dispersion of an aerosol bolus is approximated by Deff for inhalation and exhalation (25-28), which positively correlates with airway calibers and velocities of the air stream passing the bronchial tubes. In asthmatic children, calibers of proximal bronchi are reduced to a certain extent (16,18,37), which, on the other hand, results in elevated flow velocities noticeable in those airway structures (note: for a given inhalative flow rate, reduction of the airway caliber by 50% causes an increase of the flow velocity by 300%). Since both effects act as antagonists in Eqs. [1] and [2], enhancements of bolus dispersion due to asthmatic airway obstructions are only significant for certain volumetric lung depths (shallow boluses). Earlier theoretical studies on aerosol bolus dispersion in adult patients with COPD could show that, in the case of airway obstructions throughout the entire lung, bolus behaviour significantly deviates from that in healthy controls. If COPD is accompanied by alveolar emphysema, dispersion of inhaled aerosol boluses is hardly distinguishable from that in healthy subjects. Based on the results presented in these contributions it could be concluded that aerosol bolus measurements may have a diagnostic benefit for COPD patients and emphysema patients. Subjects having both disease symptoms, however, will not obtain a secured diagnosis from this clinical method (27).

From pathophysiological aspects, aerosol bolus dispersion may be regarded as a measure of convective mixing processes during inhalation and exhalation (1-6,16). In healthy subjects, the dispersion phenomenon has to be interpreted as result of mixing between inhaled and residual air. In asthmatic patients, this mixing process is usually disturbed by structural/metabolic changes within the tracheobronchial tree. These modifications among other include airway obstructions, hypersecretion of mucus, and local generation of mucous plugs (18). Since most effective mixing processes may be observed at the airway bifurcations (i.e., the junctions between parental airway and the two daughter airways), any disease-induced structural changes at these sites may have increasing effects on the aerosol dispersion behaviour. Increase of aerosol bolus skewness in asthmatic children compared to their healthy controls seems to have no plausible background at first sight, but can be also explained pathophysiologically. In general, bolus skewness performs a decrease with increasing VLD (Figure 5), because bolus peak asymmetry generated during inhalation is compensated during exhalation, whereby the grade of compensation positively correlates with the respiratory path length passed by the bolus (27,28). In asthmatic patients, any increase in flow velocity favours the production of peak asymmetries, since particles are axially dispersed to a higher extent. This effect is also supported by enhanced particle deposition observed in asthmatics. The particles being deposited on the epithelial walls are mainly withdrawn from the distal bolus half, resulting in a displacement of the bolus mode (28).

From the study presented here it may be concluded that theoretical modeling of aerosol bolus dispersion has reached a high level of accuracy in the meantime. The experimental results are supported by the hypothetical predictions insofar as diagnostic benefits of bolus inhalation experiments are only given to a very limited extent. Nevertheless, inspiration of aerosol boluses and measurement of disease-induced modifications of the exhaled boluses represent a non-invasive method for diagnosis, which needs to be improved in future studies.

Acknowledgements

Disclosure: The author declares no conflict of interest.

References

  1. Heyder J, Blanchard JD, Feldman HA, et al. Convective mixing in human respiratory tract: estimates with aerosol boli. J Appl Physiol (1985) 1988;64:1273-8. [PubMed]
  2. Brown JS, Gerrity TR, Bennett WD, et al. Dispersion of aerosol boluses in the human lung: dependence on lung volume, bolus volume, and gender. J Appl Physiol (1985) 1995;79:1787-95. [PubMed]
  3. Schulz H, Heilmann P, Hillebrecht A, et al. Convective and diffusive gas transport in canine intrapulmonary airways. J Appl Physiol (1985) 1992;72:1557-62. [PubMed]
  4. Rosenthal FS, Blanchard JD, Anderson PJ. Aerosol bolus dispersion and convective mixing in human and dog lungs and physical models. J Appl Physiol (1985) 1992;73:862-73. [PubMed]
  5. Blanchard JD. Aerosol bolus dispersion and aerosol-derived airway morphometry: assessment of lung pathology and response to therapy, Part 1. J Aerosol Med 1996;9:183-205. [PubMed]
  6. Schulz H, Eder G, Heyder J. Lung volume is a determinant of aerosol bolus dispersion. J Aerosol Med 2003;16:255-62. [PubMed]
  7. McCawley M, Lippmann M. Development of an aerosol dispersion test to detect early changes in lung function. Am Ind Hyg Assoc J 1988;49:357-66. [PubMed]
  8. Anderson PJ, Blanchard JD, Brain JD, et al. Effect of cystic fibrosis on inhaled aerosol boluses. Am Rev Respir Dis 1989;140:1317-24. [PubMed]
  9. Anderson PJ, Hardy KG, Gann LP, et al. Detection of small airway dysfunction in asymptomatic smokers using aerosol bolus behavior. Am J Respir Crit Care Med 1994;150:995-1001. [PubMed]
  10. Verbanck S, Schuermans D, Vincken W, et al. Saline aerosol bolus dispersion. I. The effect of acinar airway alteration. J Appl Physiol (1985) 2001;90:1754-62. [PubMed]
  11. Verbanck S, Schuermans D, Paiva M, et al. Saline aerosol bolus dispersion. II. The effect of conductive airway alteration. J Appl Physiol (1985) 2001;90:1763-9. [PubMed]
  12. Kohlhäufl M, Brand P, Meyer T, et al. Detection of impaired intrapulmonary convective mixing by aerosol bolus dispersion in patients with emphysema. Eur J Med Res 1997;2:121-8. [PubMed]
  13. Kohlhäufl M, Brand P, Selzer T, et al. Diagnosis of emphysema in patients with chronic bronchitis: a new approach. Eur Respir J 1998;12:793-8. [PubMed]
  14. Kohlhäufl M, Brand P, Rock C, et al. Noninvasive diagnosis of emphysema. Aerosol morphometry and aerosol bolus dispersion in comparison to HRCT. Am J Respir Crit Care Med 1999;160:913-8. [PubMed]
  15. Kohlhäufl M, Brand P, Scheuch G, et al. Aerosol morphometry and aerosol bolus dispersion in patients with CT-determined combined pulmonary emphysema and lung fibrosis. J Aerosol Med 2000;13:117-24. [PubMed]
  16. Schulz H, Schulz A, Brand P, et al. Aerosol bolus dispersion and effective airway diameters in mildly asthmatic children. Eur Respir J 1995;8:566-73. [PubMed]
  17. Keefe MJ, Bennett WD, DeWitt P, et al. The effect of ozone exposure on the dispersion of inhaled aerosol boluses in healthy human subjects. Am Rev Respir Dis 1991;144:23-30. [PubMed]
  18. Hardy KG, Gann LP, Tennal KB, et al. Sensitivity of aerosol bolus behavior to methacholine-induced bronchoconstriction. Chest 1998;114:404-10. [PubMed]
  19. Chai H, Farr RS, Froehlich LA, et al. Standardization of bronchial inhalation challenge procedures. J Allergy Clin Immunol 1975;56:323-7. [PubMed]
  20. O’Byrne PM, Samel N. Airway challenge with inhaled constrictor mediators. In: Spector SL. eds. Provocative challenge procedures: background and methodology. Mount Kisco, NY: Futura, 1989:277-91.
  21. Dubois AB, Botelho SY, Comroe JH Jr. A new method for measuring airway resistance in man using a body plethysmograph: values in normal subjects and in patients with respiratory disease. J Clin Invest 1956;35:327-35. [PubMed]
  22. Scherer PW, Shendalman LH, Greene NM, et al. Measurement of axial diffusivities in a model of the bronchial airways. J Appl Physiol 1975;38:719-23. [PubMed]
  23. Hofmann W, Koblinger L, Brand P, et al. The effect of convective mixing on particle transport in the human respiratory tract. Ann Occup Hyg 1994;38:167-74.
  24. Darquenne C, Brand P, Heyder J, et al. Aerosol dispersion in human lung: comparison between numerical simulations and experiments for bolus tests. J Appl Physiol (1985) 1997;83:966-74. [PubMed]
  25. Sarangapani R, Wexler AS. Modeling aerosol bolus dispersion in human airways. J Aerosol Sci 1999;30:1345-62.
  26. Lee JW, Lee DY, Kim WS. Dispersion of an aerosol bolus in a double bifurcation. J Aerosol Sci 2000;31:491-505.
  27. Sturm R, Pawlak E, Hofmann W. Monte-Carlo-Model for the aerosol bolus dispersion in the human lung--part 2: model predictions for the diseased lung. Z Med Phys 2007;17:136-43. [PubMed]
  28. Hofmann W, Pawlak E, Sturm R. Semi-empirical stochastic model of aerosol bolus dispersion in the human lung. Inhal Toxicol 2008;20:1059-73. [PubMed]
  29. Sturm R, Hofmann W. Stochastic simulation of alveolar particle deposition in lungs affected by different types of emphysema. J Aerosol Med 2004;17:357-72. [PubMed]
  30. Koblinger L, Hofmann W. Analysis of human lung morphometric data for stochastic aerosol deposition calculations. Phys Med Biol 1985;30:541-56. [PubMed]
  31. Raabe OG, Yeh HC, Schum GM, et al. Tracheobronchial geometry: Human, dog, rat, hamster–A compilation of selected data from the project respiratory tract deposition models. Report LF-53. Albuquerque, Lovelace Foundation, 1976.
  32. Haefeli-Bleuer B, Weibel ER. Morphology of the human pulmonary acinus. Anat Rec 1988;220:401-14. [PubMed]
  33. International Commission on Radiological Protection (ICRP). eds. Human respiratory tract model for radiological protection. Oxford: SAGE Publications, 1994.
  34. Phalen RF, Oldham MJ, Beaucage CB, et al. Postnatal enlargement of human tracheobronchial airways and implications for particle deposition. Anat Rec 1985;212:368-80. [PubMed]
  35. Segal RA, Martonen TB, Kim CS, et al. Computer simulations of particle deposition in the lungs of chronic obstroctive pulmonary disease patients. Inhal Toxicol 2002;14:705-20. [PubMed]
  36. Pedley TJ. A theory for gas mixing in a simple model of the lung. In: NATO Fluid Dynamics Panel. eds. Fluid Dynamics of Blood Circulation and Respiratory Flow. Naples, Italy: North Atlantic Treaty Organization, 1970:65.
  37. Sturm R. An advanced stochastic model for mucociliary particle clearance in cystic fibrosis lungs. J Thorac Dis 2012;4:48-57. [PubMed]
Cite this article as: Sturm R. Aerosol bolus dispersion in healthy and asthmatic children-theoretical and experimental. Ann Transl Med 2014;2(5):47. doi: 10.3978/j.issn.2305-5839.2014.04.13

Article Options

Download Citation

Share