Design, application, and evaluation of a novel method for determining optimal trajectory of thoracic pedicle screws

Introduction

Pedicle screw placement is the most commonly used method for spinal fixation and involves the screws being inserted posteriorly into the vertebral body through the long, narrow pedicle. The accuracy of screw placement is critical to the success of spinal surgery, but the placement of the thoracic pedicle screws is technically challenging and is associated with a high rate of placement failure as only one chance is available for screw placement (1,2). Moreover, any error in screw placement may cause injuries to the surrounding nerves, vessels, and the spinal cord. Screw placement is often performed under X-ray guidance [two-dimensional, (2D); three-dimensional (3D), and C-arms] and computed tomography (CT) guidance (commonly multislice spiral CT and cone beam CT). Use of navigation techniques guided by radiographic imaging and use of computer applications have significantly increased the success rate of screw placement (3-11). However, despite these advances, along with regular physician training and the refinement of surgical protocols, some errors in screw placement are often unavoidable (12-14). To solve this problem, we propose a novel method for determining the optimal trajectory for the pedicle screw placement.

To the best of our knowledge, the concept of determining optimal screw trajectory has not been reported elsewhere. Currently, the evaluation of the screw placement is conducted by indirect measures, such as cortex breach rate. In this study, we followed a systematic procedure with the following component steps to practically demonstrate the application of this novel concept: (I) trajectory design; (II) application of the design; (III) anatomical positioning; (IV) biomechanical optimization; (V) evaluation of postoperative trajectory vis-à-vis the designed trajectory.

For any given vertebra, there can only be one optimal trajectory for screw placement. However, determining the optimal trajectory and the accurate placement of screws through the optimal trajectory, is a technically challenging endeavor.

The application of digital technology has opened new vistas for orthopedic surgery and provided an opportunity for designing the optimal trajectory for the pedicle screw placement. Synergistic use of 3D visualizing software and advanced navigation techniques offer an unmatchable platform to design and apply the optimal trajectory in any position of the pedicle. In this study we aimed to investigate the design, application, and the evaluation of the optimal trajectories for the placement of thoracic pedicle screws. We present the following article in accordance with the MDAR reporting checklist (available at http://dx.doi.org/10.21037/atm-20-5426).

Methods

Materials

This experimental study was conducted on 15 adult cadavers (12 males and 3 females). The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by the Ethics Committee of the Affiliated Hospital of Putian University and informed consent was taken from all the patients. The hardware and instruments used included Dell T7500 workstation, Makerbot Replicator 2 3D printer (USA), and SIEMENS/Emotion 16 volume CT. The software used included Mimics (version 14.0) and MakerWare 3D printing software. The surgical instruments used were K-wires (Φ1.0, 1.2, 1.5, 2.0, 2.5 mm), cannulated drill (Φ2.5, 3.5, 5.0 mm), cannulated screw tap (Φ3.5, 4.5, 6.5 mm), and industrial stainless steel sunk screws (Φ3.5, 5.0, 6.5 mm; 35–80 mm; 5 mm stepping).

Three-dimensional reconstruction of CT images

The thoracic vertebrae were scanned using CT (130 KV, 21.6 mAs, pitch 0.625 mm) and exported into a 512×512 pixel DICOM format to Mimics 14.0 with the threshold range of 148 Hounsfield units to maximum. In the region growing and morphology operation menu, the parameter operation was set as “close”, and the number of pixels was set to 2, 8 – connectivity. Mask A was obtained. In calculating polylines and cavity fill from polylines, Mask B was obtained. In Boolean operations, Mask B − Mask A = Mask C. In region growing, the region outside the bone in Mask C was selected (primarily the spaces inside the vertebral canal and between the vertebral bodies) followed by Mask D. In Boolean operations, Mask B − Mask D=Mask E. Then, the mask of the vertebrae containing filled cavities in the bone was obtained without mistake selections. In “Edit Mask” in the 3D menu, the vertebral mask was partitioned at the junction between the vertebral pedicle and the vertebral body, resulting in isolated anterior vertebral bodies and the posterior appendixes.

Designing the optimal trajectory

Using the menu Med CAD/Create Cylinder, the trajectory was designed as Φ1.6 mm for thoracic vertebrae T1–T5, Φ1.8 mm for T6–T10, and Φ2.6 mm for T11–T12. The pedicle passage was maximized by manipulating the viewing angle in the transparent view. The trajectory was laid out from the anterior vertebral body to the posterior direction, through the pedicle central axis. This helped to achieve symmetry between the bilateral trajectories. The bilateral trajectories were in the same plane and were symmetrical with respect to the median sagittal plane. After all the trajectories were laid out, the linking lines on either side of the trajectories were in the same curved plane and were symmetrical to the median sagittal plane (Figure 1).

Figure 1 Overview of all the designed optimal trajectories. (A) The entry points. (B and C) The lines linking the bilateral entry points. (D) The linking lines on either side of the trajectories are in the same curved plane and are symmetrical to the median sagittal plane.

Design and printing of the navigation module

The supporting column of the navigation module was designed using the Med CAD/Cylinder menu. The trajectory was replicated and magnified to Φ10 mm, with a length of 35 mm to the bone surface.

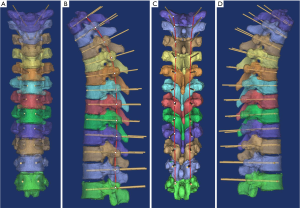
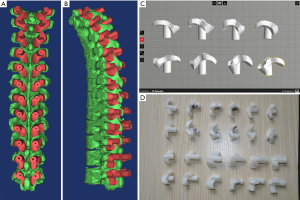
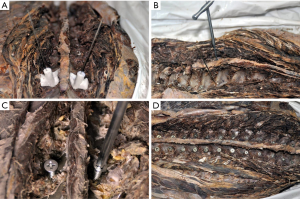
The socket module was designed using the Simulation/Cut Orthogonal to the Screen menu. The bone surface was positioned to face the operator. The posterior structures of the vertebrae were precisely trimmed (Figure 2A,B) with 1.5 mm to the superior and inferior laminae, medially to the junction of the spinous process and the lamina, and, laterally to one-half of the transverse process. The trimmed bones were replicated twice. A 4–6-mm-thick socket module was obtained using the Simulation/Reposition menu (Figure 2C). The borders of the socket module were trimmed to make the downside wider and the upside narrower. Through Boolean operations, [(socket module + supporting column) – (trajectory + vertebra)] (Figure 2D), the navigation module was obtained. The part of the supporting column protruding over the socket module was trimmed (Figure 2E,F). The transverse processes and the laminae were bound to each other, and the socket module was designed according to this structural feature and thus named “structured socketing”. The navigation modules for T1–T12 are shown in Figure 3A,B. The navigation modules were exported in the stereolithography (STL) format and printed in high resolution using MakerWare (Figure 3C,D).

Figure 2 Design of the navigation module. (A) Trimmed bone surface. (B and C) Module formation. (D) Boolean operation. (E and F) The navigation module.

Figure 3 Overview and printing of navigation module. (A and B) Overview of all navigation modules. (C) Print preview of the navigation modules. (D) The final product of the printed navigation modules.

Placement of the pedicle screws

The length of designed trajectory was measured with the Mimics interface. The length and the size of the screws were chosen according to the designed trajectory. A posterior median incision was carried out. The bone surface for the socketing of the navigation module was prepared by peeling off the periosteum. The bilateral navigation modules were socketed simultaneously. Firm socking of the navigation module to the spine was confirmed. K-wires were inserted (Φ1.0 mm for T1–T5, Φ1.2 mm for T6–T10, Φ2.0 mm for T11–T12). The inserted K-wires were examined for the positioning in the same plane and for bilateral symmetry with respect to the median sagittal plane. Then, the K-wires were removed, and the navigation modules were installed. The surgeon inserted K-wires through the trajectories of the navigation modules using an electric drill (Φ1.2 mm for T1–T5, Φ1.5 mm for T6–T10, Φ2.5 mm for T11–T12). Next, the navigation modules were removed. A cannulated drill was used to create the entry point along the K-wire (Φ2.5 mm for T1–T5, Φ3.5 mm for T6–T10, Φ5.0 mm for T11–T12). A cannulated screw tap was advanced along the K-wire to create the trajectory (Φ3.5 mm for T1–T5, Φ4.5 mm for T6–T10, Φ6.5 mm for T11–T12). The K-wires were removed, and industrial screws were inserted (Φ3.5 mm for T1–T5, Φ5.0 mm for T6–T10, Φ6.5 mm for T11–T12). If the screw was not firmly socketed, the screw was compared with the next segment K-wire and then fastened (Figure 4).

Figure 4 Placement of the thoracic pedicle screws using the navigation modules. (A) Installation of the navigation module. Bilaterally symmetrical trajectories. (B) Bilateral trajectories are in the same plane. A cannulated screw tap was used to create the trajectory. (C) The screw was not immediately fastened. (D) Completion of screw placement.

Evaluation of screw placement precision

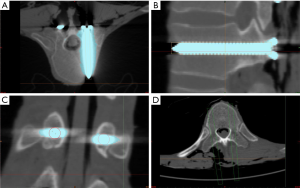
The thoracic vertebrae were examined using thin slice CT, and the images were reconstructed for 3D imaging. The 3D models of the thoracic vertebrae and the screws were merged using the Simulation/Merge menu and exported into STL format to a designed Mask . Using the command registration/point registration, the postoperative thoracic vertebral model was preliminarily fitted with the designed thoracic vertebral model. Automatic calibration was performed using the command registration/global registration, and precise fit was manually obtained using the command simulation/reposition, if necessary.

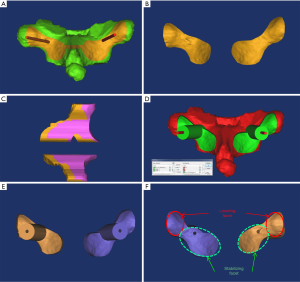
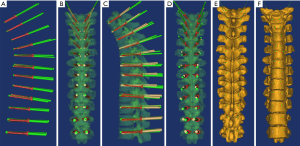
The simulation/split command was used to split the postoperative model into the bones and the screws. Using the command MedCAD/cylinder, the postoperative trajectory was modeled along the central axis of the screw, with the diameter of the placed screw (Φ3.5 mm for T1–T5, Φ5.0 mm for T6–T10, Φ6.5 mm for T11–T12) (Figure 5A,B,C,D). The images were examined for any breach of the cortex by the trajectories. The diameter of the trajectory was set to Φ0.5 mm. Using the command medCAD/point, the postoperative entry and exit points were marked at the junction between the postoperative trajectory and the designed vertebral bone surface. Using the command export txt, the 3D coordinates of the points were exported into Microsoft Excel (Figure 5E,F). The axial, sagittal, and coronal CT images of the postoperative cadavers were examined for any breach of the cortex. Artifacts created by the metals were not considered. The length of the trajectory outside the cortex was also measured (Figure 6).

Figure 5 Three-dimensional coordinates of the designed and actual entry and exit points of the screws.

Figure 6 Examination of the cortex breached by the trajectory. (A-C) The actual position of the trajectories. (D) The relative positions of the actual trajectory and the preoperative vertebra after three-dimensional fitting.

Statistical analysis

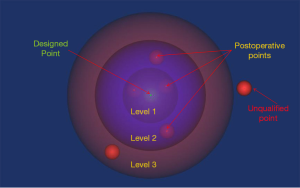
The absolute values of the preoperative and postoperative differences were analyzed. Starting from 1.1 mm, the data were screened with a 0.1 mm increment. The number and precision level of both successfully placed screws (qualified) and the mal-positioned screws (non-qualified) were analyzed. Data were compared using Chi-square text with SPSS 19.0 (SPSS, Chicago, IL, USA). A P value <0.05 was considered statistically significant. The designed and actual entry and exit points are graphically represented in Figure 7.

Figure 7 Graphical representation of the precision of screw placement.

Results

The design of trajectories through the pedicle central axis achieved symmetry between the same segments and for the whole thoracic vertebrae. A total of 358 pedicle screws were inserted of which 15 screws breached the cortex, with a length of <2 mm outside the cortex; 8 screws breached the cortex laterally, 3 breached medially, and 4 breached inferiorly into the intervertebral foramen. The absolute values of the differences in the XYZ coordinates between the designed and the actual entry points were 0.80±0.74, 0.61±0.72, and 0.72±0.58 mm, respectively; and those of the exit points were 1.53±1.30, 1.48±1.48, and 1.23±1.01 mm, respectively.

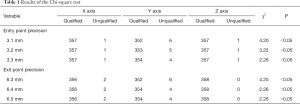
The results of Chi-square test are shown in Table 1. When the requirement of the entry point precision was ˃3.2 mm (χ²=3.22, P>0.05) and that of the exit point precision was ˃6.4 mm (χ²=2.26, P>0.05), the actual trajectory was deemed to conform to the design trajectory.

Table 1 Results of the Chi-square test
Full table

Discussion

In this study, we designed an optimal trajectory using 3D printing and navigation techniques. The traditional navigation techniques for pedicle placement inevitably involves exposure to radiation (15,16), which prevents their optimal use and further development. However, the 3D-printed navigation module does not involve radiation exposure and is more cost-effective. The inherent design flexibility, repeatability, and replicability of this methodology is especially suited to the design and verification of the optimal trajectories.

The optimal trajectory is through the central axis of the pedicle and the entering point is determined by the trajectory

With the traditional method of screw placement, it is difficult to achieve both the optimal entry point and the optimal trajectory simultaneously. In the traditional method, the entry point is first selected according to the bony anatomical marks of the posterior vertebral structures. Then, the direction and angle of the trajectory (K-wire) is adjusted using various assisting devices. Finally, the screw is inserted at the safest position. Due to the individual variations in the posterior structures of the thoracic vertebrae, there is no such thing as a fixed entry point. This is especially true in the case of patients with spinal deformities and hyperosteogeny. In practice, the optimal trajectory cannot be envisaged without determining the optimal entry point. Therefore, a major drawback of the traditional method is the lack of ability to ensure an optimal trajectory for each inserted screw. Computer-assisted designing can solve this problem of determining the optimal entry point and the optimal trajectory. Theoretically, there is only one optimal trajectory in the pedicle which can be determined using computer software without consideration of the entry point. Most previous studies have inserted the screw through the center of the pedicle (9,17,18), which was effective in preventing a breach of cortex. However, the design of trajectory for inserting the screw through the central axis of the pedicle has not been reported. We found the Mimics software as an efficient method for designing trajectory which symmetrical not only for any one single segment but also for all thoracic vertebrae. This concept can also be operationalized using other navigation techniques with preoperative design capability. The trajectory designed in our study might have caused increased abduction angle of the screw. However, due to the superficial positioning of the posterior vertebral structures, the slightly increased abduction angle does not appear to have affected the results obtained.

Unique socketing of the navigation module

The navigation technique based on rapid manufacture by 3D printing provides flexibility in design and is also free of radiation (19,20). The trajectory precision is dependent on the unique socketing between the navigation module and the bone surface. The unique socketing was achieved according to the extent of periosteal peeling which is the area of soft tissue on the bone surface that can be easily peeled while avoiding the tendon insertion points, blood vessels, and nerves. In Mimics, the bone surface was trimmed in the peeling area and the socket module was designed. Most previous studies involving a navigation module that bilateral sockets have been associated with excellent socketing (11,21-26). However, this method involves extensive peeling of the tissues between the spinous processes. Our navigation module allows for unilateral designing independent of the other side and hence does not require peeling off of tissues between the spinous processes. The socket module of our navigation module was 4–5 mm, which minimizes false socketing due to any potential deformity of the navigation module resulting from forceful manipulation. This, incidentally, is also the reason for naming it a “module” rather than a “template”.

There are various navigation tools which allow for preoperative planning. These include computer-assisted CT navigation, computer-assisted robots, frameless stereotactic technique, and a 3D printing navigation module. These navigation tools aid preoperative designing of the trajectory and allow for comparing the postoperative and preoperative trajectories. The navigation technique based on the rapid manufacture and 3D printing is technically simple, does not involve radiation exposure (20), and is associated with lower risk (23). However, the associated success rate of screw placement with this technique is unsatisfactory. The 3D-printed navigation module has an error rate of 26% associated with lumbosacral screw placement (19), a non-breach rate of 84% associated with screw placement for severe scoliosis, and a general precision of 90.8% in scoliosis (26). In the present study, only 15 (4.2%) screws breached the cortex because of ineffective socketing resulting from poor bone quality (N=8), drift in trajectory (N=5) and error in selection of screw size (N=2).

Precision and accuracy of the screw placement

It is not possible to exactly implement the planned surgical design in real-world surgery. At present, there is no gold standard for evaluating the exact implementation of surgical plans. Accuracy in preoperative designing of trajectory is essential for attaining an optimal intra-operative trajectory. Therefore, only the traditional breach rate is inadequate for the evaluation of a trajectory (9). In our study, we used both precision and accuracy to evaluate the screw placement. The differences between the real and designed entry and exit points in the 3D space are best compared using 3D coordinates. The absolute values of the differences in the XYZ coordinates between the designed and the actual entry points were 0.80±0.74, 0.61±0.72, and 0.72±0.58 mm, respectively; and the corresponding absolute difference in case of exit points were 1.53±1.30, 1.48±1.48, and 1.23±1.01 mm, respectively. The entry points showed significantly higher precision than the exit points with our navigation module. 3D spheres with different diameters were created around the preoperatively designed entry and exit points. The actual points within these spheres were deemed to have been qualified, and those outside were deemed to be disqualified. The radius of these spheres indicated the precision (Figure 7). The absolute difference between the value of the preoperative data and the postoperative data determined the precision, and the qualification rate of different levels of precision determined the accuracy. Lower precision requirements resulted in a higher qualification rate for the entry and exit points.

Conclusions

In this study, we tested a novel methodology for determining the optimal trajectory for pedicle screw placement using CT image reconstruction and 3D printing. We attained a higher level of precision and accuracy in comparison to the conventional methods. However, further investigations are required to examine the biomechanical properties associated with screw placement using this method.

Acknowledgments

Funding: This study was supported by from the Natural Science Foundation of Fujian Province (No. 2018J01194), the Research and Innovation Special Project of Putian University (No. 2019SZP03), the Fujian Province Clinical Key Specialty Construction Project (No. 2018145).

Footnote

Reporting Checklist: The authors have completed the MDAR reporting checklist. Available at http://dx.doi.org/10.21037/atm-20-5426

Data Sharing Statement: Available at http://dx.doi.org/10.21037/atm-20-5426

Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/atm-20-5426). The authors have no conflicts of interest to declare.

Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by the Ethics Committee of the Affiliated Hospital of Putian University and informed consent was taken from all the patients.

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.

References

1. Nevzati E, Marbacher S, Soleman J, et al. Accuracy of pedicle screw placement in the thoracic and lumbosacral spine using a conventional intraoperative fluoroscopy-guided technique: a national neurosurgical education and training center analysis of 1236 consecutive screws. World Neurosurg 2014;82:866-71.e1-2.
2. Bledsoe JM, Fenton D, Fogelson JL, et al. Accuracy of upper thoracic pedicle screw placement using three-dimensional image guidance. Spine J 2009;9:817-21. [Crossref] [PubMed]
3. Motiei-Langroudi R, Sadeghian H. Assessment of pedicle screw placement accuracy in thoracolumbosacral spine using freehand technique aided by lateral fluoroscopy: results of postoperative computed tomography in 114 patients. Spine J 2015;15:700-4. [Crossref] [PubMed]
4. Sugimoto Y, Ito Y, Tomioka M, et al. Clinical accuracy of three-dimensional fluoroscopy (IsoC-3D)-assisted upper thoracic pedicle screw insertion. Acta Med Okayama 2010;64:209-12. [PubMed]
5. Ravi B, Zahrai A, Rampersaud R. Clinical accuracy of computer-assisted two-dimensional fluoroscopy for the percutaneous placement of lumbosacral pedicle screws. Spine (Phila Pa 1976) 2011;36:84-91. [Crossref] [PubMed]
6. Fuster S, Vega A, Barrios G, et al. Accuracy of pedicle screw insertion in the thoracolumbar spine using image-guided navigation. Neurocirugia (Astur) 2010;21:306-11. [Crossref] [PubMed]
7. Eck JC, Lange J, Street J, et al. Accuracy of intraoperative computed tomography-based navigation for placement of percutaneous pedicle screws. Global Spine J 2013;3:103-8. [Crossref] [PubMed]
8. Ammirati M, Salma A. Placement of thoracolumbar pedicle screws using O-arm-based navigation: technical note on controlling the operational accuracy of the navigation system. Neurosurg Rev 2013;36:157-62; discussion 162. [Crossref] [PubMed]
9. Togawa D, Kayanja MM, Reinhardt MK, et al. Bone-mounted miniature robotic guidance for pedicle screw and translaminar facet screw placement: part 2--Evaluation of system accuracy. Neurosurgery 2007;60:ONS129-39; discussion ONS39.
10. Bourgeois AC, Faulkner AR, Bradley YC, et al. Improved Accuracy of Minimally Invasive Transpedicular Screw Placement in the Lumbar Spine with Three-dimensional Stereotactic Image Guidance: A Comparative Meta-analysis. J Spinal Disord Tech 2015;28:324-9. [Crossref] [PubMed]
11. Lu S, Zhang YZ, Wang Z, et al. Accuracy and efficacy of thoracic pedicle screws in scoliosis with patient-specific drill template. Med Biol Eng Comput 2012;50:751-8. [Crossref] [PubMed]
12. Sheha ED, Gandhi SD, Colman MW. 3D printing in spine surgery. Ann Transl Med 2019;7:S164. [Crossref] [PubMed]
13. Gelalis ID, Paschos NK, Pakos EE, et al. Accuracy of pedicle screw placement: a systematic review of prospective in vivo studies comparing free hand, fluoroscopy guidance and navigation techniques. Eur Spine J 2012;21:247-55. [Crossref] [PubMed]
14. Mason A, Paulsen R, Babuska JM, et al. The accuracy of pedicle screw placement using intraoperative image guidance systems. J Neurosurg Spine 2014;20:196-203. [Crossref] [PubMed]
15. Smith HE, Welsch MD, Sasso RC, et al. Comparison of radiation exposure in lumbar pedicle screw placement with fluoroscopy vs computer-assisted image guidance with intraoperative three-dimensional imaging. J Spinal Cord Med 2008;31:532-7. [Crossref] [PubMed]
16. Villard J, Ryang YM, Demetriades AK, et al. Radiation exposure to the surgeon and the patient during posterior lumbar spinal instrumentation: a prospective randomized comparison of navigated versus non-navigated freehand techniques. Spine (Phila Pa 1976) 2014;39:1004-9. [Crossref] [PubMed]
17. Ughwanogho E, Patel NM, Baldwin KD, et al. Computed tomography-guided navigation of thoracic pedicle screws for adolescent idiopathic scoliosis results in more accurate placement and less screw removal. Spine (Phila Pa 1976) 2012;37:E473-8. [Crossref] [PubMed]
18. Pechlivanis I, Kiriyanthan G, Engelhardt M, et al. Percutaneous placement of pedicle screws in the lumbar spine using a bone mounted miniature robotic system: first experiences and accuracy of screw placement. Spine (Phila Pa 1976) 2009;34:392-8. [Crossref] [PubMed]
19. Merc M, Drstvensek I, Vogrin M, et al. Error rate of multi-level rapid prototyping trajectories for pedicle screw placement in lumbar and sacral spine. Chin J Traumatol 2014;17:261-6. [PubMed]
20. Li X, Zhang Q, Zhao C, et al. Surgical application of pedicle drill template navigation technology for complicated scoliosis. Zhonghua Yi Xue Za Zhi 2014;94:840-3. [PubMed]
21. Lu S, Xu YQ, Zhang YZ, et al. A novel computer-assisted drill guide template for lumbar pedicle screw placement: a cadaveric and clinical study. Int J Med Robot 2009;5:184-91. [Crossref] [PubMed]
22. Lu S, Xu YQ, Chen GP, et al. Efficacy and accuracy of a novel rapid prototyping drill template for cervical pedicle screw placement. Comput. Aided Surg. 2011;16:240-8. [Crossref] [PubMed]
23. Ma T, Xu YQ, Cheng YB, et al. A novel computer-assisted drill guide template for thoracic pedicle screw placement: a cadaveric study. Arch Orthop Trauma Surg 2012;132:65-72. [Crossref] [PubMed]
24. Lu S, Xu YQ, Zhang YZ, et al. Rapid prototyping drill guide template for lumbar pedicle screw placement. Chin J Traumatol 2009;12:177-80. [PubMed]
25. Lu S, Xu YQ, Zhang YZ, et al. A novel computer-assisted drill guide template for placement of C2 laminar screws. Eur Spine J 2009;18:1379-85. [Crossref] [PubMed]
26. Wu ZX, Huang LY, Sang HX, et al. Accuracy and safety assessment of pedicle screw placement using the rapid prototyping technique in severe congenital scoliosis. J Spinal Disord Tech 2011;24:444-50. [Crossref] [PubMed]

(English Language Editor: J. Gray)