Automatic identification of compressions and ventilations during CPR based on the fuzzy c-means clustering and deep belief network

Introduction

The importance of uninterrupted and effective chest compressions (CCs) is critical in cardiopulmonary resuscitation (CPR) (1,2). The compression release rate, compression duty cycles, ventilation cycles, and other ventilation parameters during CCs are imperative for ensuring the quality of CPR (3-5). Unnecessary interruption of compressions during CPR can be avoided by using CC detection and real-time feedback (6). Furthermore, compression detection based on Transthoracic impedance (TTI) signals allows for an accurate estimation of the CC rates and CC pauses, and has enhanced the success rate of CPR (7).

TTI signals are acquired by sending alternating current between defibrillation electrodes and measuring the voltage changes when the current flows through the chest of patient (8).The changes in thoracic impedance during CPR, including the changes induced by thoracic deformation during compression and the variations in blood flow in the heart and vessels could be reflected by TTI signals (9). This signal has been proposed to measure the CC rates and the chest compression fraction of CPR (10). Our previous studies have found that the amplitude change of TTI was correlated with compression depth and coronary perfusion pressure and the TTI could serve as an indicator to estimate quality of chest compression (11). The compression rate and the instantaneous compression frequency can also be assessed using TTI signals during CPR (12,13). The detection and analysis of TTI signals can provide information for guiding CCs and improve the performance of CPR (11,14). In addition, the TTI is the only signal during CPR where compression and ventilation waves are concurrently visible (15), which facilitated a valuable method to discriminate the compressions activity from the ventilations activity in the TTI waveform. Prior investigations commonly used the onset of inspiration and the onset of expiration (TTI peak) as the features of detecting ventilation (16). However, ventilation induced changes of TTI signal was influenced by the corresponding airway pressure and tidal volume curves (15). Thus it is unclear if the onset of expiration could be accurately identified. Recently, the amplitude and duration of TI fluctuations was regarded as the features to automatically identify the CC (17). In fact, these limited features were too simple to guarantee excellent classification accuracy in real-time detection.

The algorithms for CCs and ventilations detection based on the TTI signals have been widely employed. The adaptive threshold method has traditionally been employed to analyze the compression waveforms, however, it has proven difficult to analyze complex waveforms using this method (18). The neural network method has also been commonly applied to recognize ventilation waveforms, though it is too time consuming to meet the requirements of real-time processing and cannot identify some specific signals (19). Xiang used traditional linear discriminant analysis (LDA) to mark the waveforms of compressions and ventilations and found that LDA requires a high signal-to-noise ratio to conduct waveform recognition (20), and is thus not suitable for processing and classifying random TTI fluctuations.

The fuzzy c-means (FCM) clustering method was first introduced by Dunn (21), and was later improved by Bezdek (22). Nayak not only proved the convergence of the algorithm, but also delivered an optimization algorithm based on the least squares iteration of this method (23). The FCM, as one typical algorithm in pattern recognition, has been achieved great performance in many aspects. For example, FCM clustering was proved to be fast and efficient for big data analysis of vehicle classification (24). Besides image segmentation, this algorithm is also significantly effective in classification of bioelectrical signal such as electrocardiogram beats (25). The deep belief network (DBN) is established on the basis of the restricted boltzmann machine (RBM), using the backpropagation algorithm for optimization. DBN has been shown to overcome the problems of traditional neural networks, such as the slow training speed and the tendency to be trapped in the local minimum value, and has also demonstrated superior performance compared to traditional methods in many aspects. The DBN was employed to identify the synthetic aperture radar image, extract emotional features of speech signals and diagnose Parkinson disease by using speech signal (26-28). The fast inference and the higher order network structures of DBN would get better performance in real-time detection of CCs and ventilations compared to the algorithms mentioned above.

To assess the quality of CPR, we proposed real-time automatic detection analysis of TTI signals based on wavelet analysis using the FCM clustering and DBN methods. Firstly, the TTI signals were preprocessed using a denoising algorithm. The potential compression and ventilation waveforms were then marked using a search algorithm with a multi-resolution window. The width, amplitude, and differences between the marked waveforms and their adjacent waveforms were selected as features. The signals were divided into several sections according to the width of the marked waveforms. Next, the original signals were decomposed using wavelets and the energy of each section of a wavelet was extracted. The ratio of the energy of each section to the original signal amplitude was taken as a feature. The features of the waveform were represented by a four-dimensional vector. The FCM clustering method was subsequently utilized to recognize and classify the compression and ventilation segments of the marked waveforms. Finally, the recognition results were compared with those obtained by the adaptive threshold method, the neural network method, and LDA to demonstrate the superiority of the proposed algorithm. The possibility of TTI signals as an indicator in monitoring the quality of chest compressions has been demonstrated in our previous investigation. This study focuses on applying the pattern recognition algorithm to detect the CCs and ventilations using the TTI signal, which could evaluate the CPR quality and improve the success rate of CRP in real-time. We first proposed to use the FCM clustering and DBN methods to classify the CCs and ventilations using TTI signals, which overcomes the deficiency that the traditional algorithms are too time consuming to identify the waveforms and cannot detect the complex waveforms. This is an extension of our previous study.

We present the following article in accordance with the ARRIVE reporting checklist (available at http://dx.doi.org/10.21037/atm-20-5906).

Methods

Experimental data

Data collection

The experimental data were provided by the Institute of Surgical Research of Daping Hospital, the Third Military Medical University in Chongqing, China. This study was carried out in strict accordance with the recommendations in the Guidance for the Care and Use of Laboratory Animals of the National Institutes of Health. The protocol was approved by the Animal Ethics Committee (Permit Number: IAEC-2011-0701), Sun Yat-sen University, Guangzhou, China.

Data was collected from a cardiac arrest model that electrically induced cardiac arrest in pigs. In total, 16 healthy adult boars of matched weight (18–22 kg in weight) were included in the study. The unhealthy animals or the animals with abnormal physiological parameters were excluded from the analysis. The purchased domestic pigs were fed in the laboratory for more than one day to ensure the physiological parameters to be stable. The experimental animals have fasted before the experiments, but they have free access to water. The Anesthesia was initiated by intramuscular injection of ketamine (20 mg/kg) and completed by ear vein injection of sodium pentobarbital (30 mg/kg). Tracheal intubation was conducted immediately after anesthesia and the animals were mechanically ventilated with a volume-controlled ventilator (model Avs III, T Bird, CA, USA). In order to measure the aortic pressure, a 6Fr fluid-filled angiographic catheter was advanced from the surgically exposed right femoral artery into the thoracic aorta. For measurements of right atrial pressure and pulmonary arterial pressure, a 7-Fr, pentalumen, thermodilution-tipped catheter was advanced from the surgically exposed right femoral vein and flow-directed into the pulmonary artery. A 5-Fr pacing catheter (Cordis Corporation, Miami Lakes, FL, USA) was advanced into the right ventricle to induce the ventricular fibrillation (VF) electrically. In order to collect TTI signals, a pair of defibrillation pads (stat-padz, Zoll Medical Corporation, Chelmsford, MA, USA) was stuck to the front chest anteriorly to laterally and a circuit with a sinusoid-wave excitation current of 2 mA and 30 kHz was parallelly connected to the defibrillation pads. The TTI signals of the pig were measured (upon stabilization of physiological parameters) using the WinDaq data acquisition system (DATAQ Instruments Inc., Akron, OH, USA) with a sampling frequency of 300 Hz.

Experimental procedures

VF was induced by applying a 2 mA alternate current through the 5-Fr pacing catheter. The cardiac arrest was confirmed when VF sustained for 30 seconds after the electrical stimulation and the arterial blood pressure was below 40 mmHg. Since the VF has been successfully induced, mechanical ventilation was removed and cardiac arrest was lasted for 6 minutes. Then, the CRP was performed by an emergency medical doctor at a rate of 100 per min. The compression depth was set to 25% of the anterior posterior diameter of the chest. The CC fraction was 50% and the interruptions in compressions were avoided. The bag-valve device was applied to provide the ventilation for animals during CPR. Chest compression was synchronized to provide a compression/ventilation ratio of 30:2 with equal compression-relaxation intervals. After 2 minutes of CC, a single 120 J rectilinear biphasic shock (M-Series, Zoll Medical Corporation, Chelmsford, MA, USA) was used for defibrillation. The following electrocardiogram analysis was preformed until the confirmation of spontaneous circulation. The defibrillation was thought to be successful when the VF conversion to an organized rhythm that generates arterial pressure pulsation ≥60 mmHg for an interval ≥10 s. If spontaneous circulation was not restored, CC was continued for another 2 minutes, after which defibrillation was attempted with another single 120 J shock. This sequence was repeated for a maximum of 5 cycles. Catheters were removed after 1 h of post resuscitation monitoring, and the animals were euthanized by injection of 150 mg/kg intravenous pentobarbital. The details of the animal experiments have been described in our previous studies (11).

Signal data

The quality of CPR decreases as time passes, which ultimately affects its success rate (29). So, data from the first 2 minutes is more effective and widely used in evaluating the quality of CPR (30). In an actual rescue of drowning or asphyxiating cardiac arrest patients, five cycles (2 minutes) of CPR should be administered before initiating the emergency medical service system. Thus, data from the first 2 minutes of CPR were acquired as a dataset in our study, and contained a continuous signal waveform.

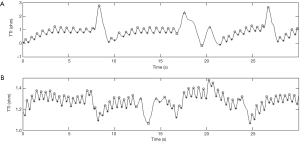
The mean compression rate was 100 compressions per minute and the CC fraction was 50%. The compression to ventilation ratio was 30:2 and interruptions in compressions were avoided (except for ventilations). Each ventilation lasted for no longer than one second to avoid excessive ventilation. A continuous waveform with a peak-and-trough indicated a CC in the TTI signals (31). For each compression, the amplitude change of the TTI signals was described by the difference between the adjacent peak and trough of an impedance waveform. Examples of segments of TTI signals collected in this experiment are shown in Figure 1. Figure 1A shows an example of standard signal waveforms in which the compression segments were easily distinguishable from the ventilation segments. As seen in Figure 1B, part of the compression waveform was similar to the ventilation waveform due to abnormal compressions. In Figure 1C, some of the signals were difficult to identify on account of the interference of high-frequency noises and a baseline drift.

Figure 1 The segment examples of TTI signals collected in this experiment. (A) The waveforms of a standard signal; (B) an abnormal signal; (C) a signal affected by noise and baseline drift. TTI, transthoracic impedance.

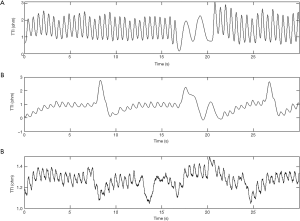
Automatic detection algorithms of the thoracic impedance signals

Waveform analysis based on a multi-resolution window search method

Interferences in TTI signals were mainly caused by high-frequency noises and a baseline drift. High-frequency noises have a sharp waveform and small amplitude. Noises and interferences can be eliminated by denoising and smoothing to obtain clearer signals. We considered TTI fluctuations as a function of the sampling points and defined the function as f(). Theoretically, the peaks and troughs of TTI fluctuations could be found by an extremum search. Since some pseudo and composite waves were caused by multiple interferences, the conventional optimization methods (local optimization method) were no longer valid for analyzing the wavelets.

Multi-resolution analysis is an effective signal processing method that adopts different resolutions to process the same signal. Using this method, the local optimal values under different resolutions can be determined and combined to obtain more precise optimal values. Assuming that there were n resolutions, the widths of the search window varied in the multi-resolution analysis. In this study, three resolutions (n=3) were analyzed and the widths of each search window were set to 20, 40, and 60. To identify whether p_i was an extremum point, a search was performed in the first resolution using the following equations:

$$f(p_i)=\max (f(p_{i-10},p_{i-9},\cdots p_i,\cdots ,p_{i+9},p_{i+10}))$$[1]

$$f(p_i)=\min (f(p_{i-10},p_{i-9},\cdots p_i,\cdots ,p_{i+9},p_{i+10}))$$[2]

If the left side was equal to the right side of Eq. [1] or Eq. [2], then the weight k was considered as k = k +1 (initial k value was 0 in each search). Searches were then performed under other resolutions. If k >0.5n, then the point p_i was determined as a peak or a trough point.

For the data of each pig, although all peaks and troughs could be identified by the multi-resolution window search method, there may be a small amount of pseudo local extremum points. Pseudo local extremum points induced by pseudo and composite waveforms should be eliminated. With our prior knowledge, we extracted the amplitudes (the amplitude difference between neighboring wave peaks and troughs) and time spans (the distance of neighboring peaks and troughs) of signal waveforms as features. After identifying every potential peak or trough, the average amplitude and time distance between adjacent peaks or troughs were calculated and represented as M_ad and M_td, respectively. The amplitude distance (D_a) and time distance (D_t) of each neighboring peak and trough were compared to M_td and M_td. For the convenience of calculation, we assumed the amplitude distance and time distance of the i_th adjacent peak and trough were D_ai and D_ti, respectively. If D_ai < m · M_ad or D_ti < m · M_td (where m denotes the threshold coefficient, m =0.1), then the peak or trough was considered to be wrong.

Feature extraction

Extraction of characteristics of TTI fluctuations

After the peaks and troughs of the TTI fluctuations were labeled exactly, the width L and amplitude H of each section of waveform were obtained. The waveforms were divided into sections according to their width. When the CCs matched the internationally prescribed ventilation ratio of 30:2, we found that most of the ventilations were double-period waves and were different from the compression waves in Figure 1. Feature differences between neighboring waveforms were extracted as a new feature. The feature difference of the n_th waveform was:

$$Dif(n)=(\frac{H(n)}{H(n-1)}+\frac{H(n)}{H(n+1)})+(\frac{L(n)}{L(n-1)}+\frac{L(n)}{L(n+1)})$$[3]

Feature extraction based on wavelet decomposition

Wavelet analysis is a powerful time-frequency localization method. Translation and scaling of wavelet functions allows for a signal to be denoted by the sum of various sub-bands in the time and frequency domains. Using this method, we can detect certain frequency characteristics of the original signals. Figure 1 illustrates that the waveform of the compression segment had a width of approximately 0.5 s, which was evidently different from the ventilation segment. We highlighted the features of the compression segments and weakened the ventilation segments through wavelet decomposition to distinguish the compression and ventilation waveforms. An example of wavelet decomposition under different scales is shown in Figure 2.

Figure 2 Detailed wavelet coefficients. (A) The 1st level; (B) the 2nd level; (C) the 3rd level; (D) the 4th level; (E) the 5th level; (F) the 6th level; (G) the 7th level; (H): the 8th level; (I) the 9th level.

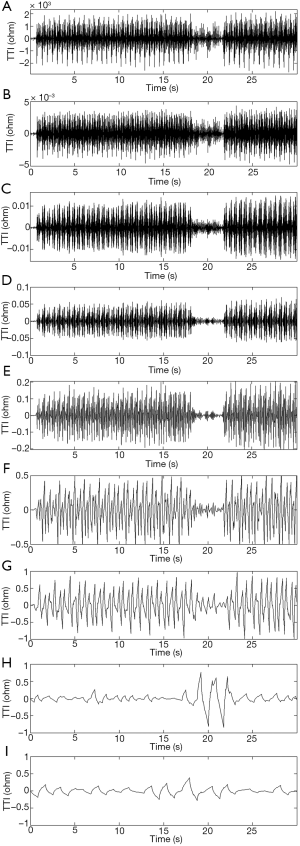
Based on the principle of wavelet decomposition frequency division, a TTI signal was extracted with discrete wavelet decomposition, making each sub-band a dichotomy of frequency domains from high frequencies to low frequencies. If the frequency space of the original signal showed V₀ = [0, f_s / 2], then the frequency space of the wavelet coefficients in the first level was W₁= [2^–1, f_s, f_s], and the frequency space of the wavelet coefficients in the second level was W₂= [2^–2, f_s, 2^–1f_s]. By parity of reasoning, the frequency space of the wavelet coefficients in the Nth level was W_N = [2^–N, f_s, 2^–N+1f_s], where f_s denotes the sampling rate of the TTI signal.

The frequency of ventilations was lower than that of compressions. The corresponding frequency was:

$$f_V=f_s/n$$[4]

where n denotes the number of samples of ventilation waveforms. Therefore, with a level number i, the frequency was:

$$f_V\in [2^{-i}{f}_s,2^{-i+1}{f}_s]$$[5]

Thus, the features of ventilation could be reflected in the i_th level of the wavelet decomposition.

The number of samples of the ventilation waveform was between 400 and 600. According to Eq. [4], the frequency in relation to the width of the ventilation waveform was f_V = f_s / n =300/600=0.5. According to Eq. [5], the features of this waveform fell into the range of the sub-band in the ninth level; therefore, the number of optimal decomposition levels was nine. The original signal (a) was decomposed by nine-level wavelet decomposition with a Daubechies 2 (db2) wavelet.

Following wavelet decomposition of the original signals (in the detailed wavelet function of the 5th level), we found that the compression and ventilation segments were different in the waveforms of wavelet coefficients. Moreover, compression waveforms with smaller amplitudes in the TTI fluctuations had corresponding smaller wavelet coefficients. In order to remove such interferences, the ratio of the original waveform’s amplitude to the energy of the 5th wavelet coefficient was selected as a feature in a certain section of the original waveform.

$$D_w=H(n)/p(n)$$[6]

where H(n) denotes the amplitude of the nth section of the original waveform and p(n) denotes the energy of the 5th wavelet coefficient. The feature curve of D_w of the standard signal (a) is shown in Figure 3.

Figure 3 Feature curve of discrete wavelet transform Dw; the ratio of the original waveform’s amplitude to the energy of the 5th wavelet coefficient.

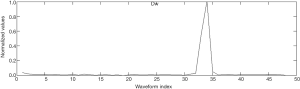
The feature D_w of the ventilation waveform was larger than that of the compression waveform. Therefore, D_wwas considered as a basis for classification.

Normalization

After the two feature extractions above were described, we obtained a four-dimensional feature vector that included width L, amplitude H, difference of features, and the ratio of amplitude to the energy of the wavelet coefficient D_w. Since each feature shared the same weight, linear normalization was applied.

$$x_{nor}(n)=\frac{x(n)-\min (x)}{\max (x)-\min (x)}$$[7]

where x_nor(n) are the normalization results and x(n) are the features. The value of features was normalized to a range of zero to one.

Classification and identification

The pseudo and composite waves were automatically excluded from the analysis after processed by the characteristics extraction and wavelet decomposition. The FCM clustering and DBN methods were used in classification and identification to mark the waveforms of compressions and ventilations. To obtain results with high generalization in FCM clustering, the compression-ventilation ratio 30:2 was used as a priori knowledge to modify the identification. In DBN, the 10-fold cross-validation was used. A random group of pigs were used to validate the algorithm, while the remaining pigs were used to study the algorithm. There was no overlapping between the training set and the validation set. Two neighboring wave troughs were used to identify a waveform and the data from each pig consisted of multiple waveforms.

FCM clustering analysis

The FCM algorithm achieves the optimal partition of samples by minimizing the objective function. For instance, suppose that we have n samples that could be clustered into c classes. In this case, the objective function is $J={\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^c{\mu }_{ij}^m}\Vert x_i-v_j\Vert \stackrel{2}{}$, which satisfies the constraint condition ${\displaystyle \sum _{j=1}^c{\mu }_{ij}^{}}=1$. Here, x_i is the vectors of feature for sample i, V_j is the clustering center of class j, μ_ij is the membership degree of sample i to class j, and m is the weighting function. The FCM algorithm optimizes the objective function by updating V_j and μ_ij. According to the extreme value theory of Lagrange multipliers, the updated formulas were defined as:

$${\mu }_{ij}^{}=\frac{1}{{{\displaystyle \sum _{k=1}^c\left(\frac{\Vert x_i-v_j\Vert }{\Vert x_i-v_k\Vert }\right)}}^{\frac{2}{m-1}}}$$[8]

$$v_j=\frac{{\displaystyle \sum _{i=1}^n{\mu }_{ij}^m{x}_i}}{{\displaystyle \sum _{i=1}^n{\mu }_{ij}^m}}$$[9]

When the equation: $|J_t-J_{t-1}|<\epsilon$ is satisfied by the obtained value of the target function after two adjacent rounds of iteration, the updating is stopped because an acceptable clustering result is achieved. The sign of ε is a very small positive number, namely, the allowable error. Finally, based on the maximum membership degree principle, the samples are categorized into a class according to its maximum membership degree (32,33).

DBN

The DBN is a probabilistic generative model composed of stacked RBMs [21] (34). A RBM is a bipartite undirected graphical model (i.e., a type of Markov random field) that describes the dependency among a set of random variables with a two-level architecture (35). In this model, the visible stochastic units $v\text{=}{\left[v_1,\mathrm{..},v_V\right]}^T$ are connected to the hidden stochastic units $h\text{=}{\left[h_1,\mathrm{..},h_H\right]}^T$. V denotes the number of units of the visible levels, while H signifies those of the hidden levels, and (.)^T indicates the matrix transpose. Assuming that $v\in {\left\{0,1\right\}}^v$ and $h\in {\left\{0,1\right\}}^H$, each visual node is independent of the other visual nodes and is connected with hidden nodes. Also, each hidden node is only affected by visual nodes, which makes it easy to train a RBM. The model parameters are composed of $a\text{=}{\left[a_1,\mathrm{..},a_V\right]}^T$, $b\text{=}{\left[b_1,\mathrm{..},b_V\right]}^T$, and $W\text{=}{\left\{w_{ij}\right\}}_{V\times H}$. According to the parameters, RBM encodes sample x as the following rule: given that $x\text{=}(x_1,x_2,\mathrm{..},x_n)$, the sample was encoded to $y\text{=}(y_1,y_2,\mathrm{..},y_n)$. The probability of the j^th feature values for one of hidden nodes is computed as:

$$p(h_j=1|v)=\sigma ({\displaystyle \sum _{i=1}^n{w}_{ij}\times v_i+b_j})$$[10]

where the value of v is x and h_j is y_j. That is, the probability of the j^th position value for one of sample y is p(h_j = 1|v). Here, v is a training sample, and h_j is the class label (when there is only one hidden node, the probability of the hidden node value is one). The RBM can be used for classification.

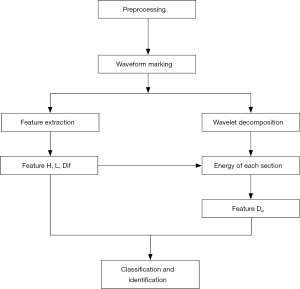
Flow chart of automatic detection algorithm of TTI signals

The flow chart of the algorithm is shown in Figure 4. This algorithm is conducted according to the following steps:

• The high frequency noise was removed using wavelet denoising combined with a moving average filter.
• Compression and ventilation waveforms were marked with the multi-resolution window search. The extracted features included the width L, amplitude H, and the feature difference between neighboring waveforms Dif.
• TTI signals were decomposed and preprocessed by wavelet decomposition. The ratio of the original waveform’s amplitude to the energy of the 5th wavelet coefficient is defined as D_w.
• The four-dimensional feature vector (including the L, H, Dif, and D_w) of the waveform was obtained and normalized.
• The FCM clustering and DBN methods were applied to identify and classify the compressions and ventilations in the marked waveforms.

Figure 4 Flow chart of automatic detection algorithm of TTI signals. This algorithm is conducted with preprocessing, waveform marking, wavelet decomposition and other steps. TTI, transthoracic impedance.

Results

The identification of compression and ventilation waveforms

The classification results of the abnormal signal (Figure 1B) and the signal affected by noise and baseline drift (Figure 1C) are shown in Figure 5. The circles and stars represent the peaks and troughs of compression waveforms, respectively, and the triangles and squares represent the peaks and troughs of ventilation waveforms, respectively. All compression waveforms were identified (in the rectangle). The isolated pseudo compression waveforms were not identified, demonstrating that the pseudo waveforms could be effectively eliminated.

Figure 5 Classification results of original data. (A) An abnormal signal (original data: Figure 1B); (B) a signal affected by noise and baseline drift (original data: Figure 1C). The circles and stars represent the peaks and troughs of compression waveforms, respectively. The triangles and squares represent the peaks and troughs of ventilation waveforms, respectively. TTI, transthoracic impedance.

The positive predictive value and sensitivity for classifiers

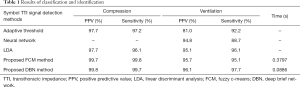
The recordings included in this study were collected from 16 pigs that underwent electrically induced cardiac arrest and subsequent CPR. For each pig, the positive predictive value (PPV), the sensitivity of recognition, and the time cost were calculated using the FCM clustering and DBN methods for compression and ventilation, respectively. In order to verify the performance of the proposed algorithm, other relative algorithms were chosen for comparison.

For FCM clustering, the PPVs of compression and ventilation were 99.7% and 95.7%, respectively, and for DBN, these values were 99.8% and 96.1%, respectively. Furthermore, for FCM clustering, the recognition sensitivities of compression and ventilation were 99.8% and 95.1%, respectively, and for DBN, these values were 99.7% and 97.7%, respectively. The average running time to process each group of datum (36,000 sampling points) was 0.3797 and 0.0886 s for FCM and DBN, respectively (Table 1). The classification and identification of TTI signals were conducted to denoise and eliminate pseudo waves. The PPV and recognition sensitivity obtained by our analysis were higher than both the adaptive threshold (18) and neural network (19) methods.

Table 1 Results of classification and identification
Full table

Discussion

In this study, we proposed two real-time automatic detection algorithms (FCM clustering and DBN) for TTI signals. We used wavelet decomposition to preprocess the signals and identify the compression and ventilation waveforms (morphological and wavelet features) to evaluate CPR quality. The proposed algorithms effectively eliminated the majority of interferences caused by distortions and noise, and precisely identified the compression and ventilation waveforms. Real-time feedback of compression and ventilation information can be provided to a rescuer to guide CPR. Our findings suggest that FCM clustering and DBN methods can be used to effectively and accurately evaluate CPR quality and provide information for improving the success rate of CPR.

Comparison of different algorithms

The conventional methods have some disadvantages in the detection of TTI signals. For the neural network method, pseudo ventilation waveforms were found in the ventilation segments, however the neural network method has a low capacity of anti-pseudo-waves processing. For the adaptive threshold method, the parameters were fixed, while the features of compression and ventilation varied across different TTI signals. Hence, the fixed parameters might have failed to accurately classify and identify the waveforms. The low capacity of these methods for processing anti-pseudo waves will lead to unsatisfactory identification results. LDA seemed to be adequate for classification, however, it was difficult to estimate the time cost using this approach, which is a critical factor for evaluating a TTI detection algorithm. Compared to the aforementioned methods, the FCM clustering and DBN methods proposed in this study had a relatively high accuracy and low time cost.

Automatic detection of the TTI signal is essential for classification. The TTI signals had minimum fluctuations and drifts, and thus, pseudo peaks and troughs might interfere with TTI signals processed using a conventional method of extremum or local optimization. The extremum judgment with multi-resolution can reduce pseudo peaks and troughs. Though, in general, it is challenging to differentiate between the compressions and ventilations, and better features are needed. Through multilevel wavelet decomposition, we found that the differences between compression and ventilation waves were amplified by wavelet features, and the accuracy of classification was improved. In addition, using this method allowed us to calculate the time cost, which was not addressed in previous studies. Furthermore, our study was the first to use DBN in TTI detection, and the results were exceptional in both accuracy and time cost. Our method provided a real-time automatic detection of TTI signals. Also, methods such as the neural network are not suitable for dense samples; a certain amount of training time is needed to determine weights. In contrast, the FCM clustering and DBN methods can balance the accuracy and time cost by adapting weights.

Limitations and future directions

Although this study applied the FCM clustering and DBN methods to detect the compression and ventilation using TTI signals from pigs, there were two noteworthy limitations to our investigation. Firstly, the compression to ventilation ratio in this animal experiment was set at 30:2 to guarantee that CPR was delivered in a prescribed and controlled way. However, CPR patterns vary. For instance, compression-only (i.e., without ventilation) CPR and longer interruptions occur frequently, and the compression to ventilation ratio is not fixed. Hence, the applicability of the proposed method may be limited. In future studies, we intend to explore this method with other CPR patterns to uncover its applicability. Secondly, the disconnections, defibrillation, and pause were not included in the TTI signals in this study. However, these events are critically important during CPR in people. It is therefore crucial that future datasets include many other events and a greater number of samples to detect compression and ventilation, which may ultimately contribute to improving the success rate of CPR.

Acknowledgments

Funding: The research was supported by the Chongqing Technology and Innovation Program of Social and Livelihood (cstc2016shmszx130014, HHZ) and the Youth Training Project of Army Medical Technology (13QNP120, HHZ) by the Training Project of Army Medical University for Research Talents in Clinical Medicine (2018XLC3066).

Footnote

Reporting Checklist: The authors have completed the ARRIVE reporting checklist. Available at http://dx.doi.org/10.21037/atm-20-5906

Data Sharing Statement: Available at http://dx.doi.org/10.21037/atm-20-5906

Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/atm-20-5906). The authors have no conflicts of interest to declare.

Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. This study was carried out in strict accordance with the recommendations in the Guidance for the Care and Use of Laboratory Animals of the National Institutes of Health. The protocol was approved by the Animal Ethics Committee (Permit Number: IAEC-2011-0701), Sun Yat-sen University, Guangzhou, China.

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.

References

1. Hirose T, Iwami T, Ogura H, et al. Effectiveness of a simplified cardiopulmonary resuscitation training program for the non-medical staff of a university hospital. Scand J Trauma Resusc Emerg Med 2014;22:31. [Crossref] [PubMed]
2. Alalwan A, Ehlenbach WJ, Menon PR, et al. Cardiopulmonary resuscitation among mechanically ventilated patients. Intensive Care Med 2014;40:556-63. [Crossref] [PubMed]
3. Russell JK, González-Otero DM, Ruiz de Gauna S, et al. Can chest compression release rate or recoil velocity identify rescuer leaning in out-of-hospital cardiopulmonary resuscitation? Resuscitation 2018;130:133-7. [Crossref] [PubMed]
4. Cortegiani A, Baldi E, Iozzo P, et al. Real-time feedback systems for cardiopulmonary resuscitation training: time for a paradigm shift. J Thorac Dis 2018;10:E162-3. [Crossref] [PubMed]
5. Kramerjohansen J, Edelson DP, Losert H, et al. Uniform reporting of measured quality of cardiopulmonary resuscitation (CPR). Resuscitation 2007;74:406-17. [Crossref] [PubMed]
6. Lin S, Scales DC. Cardiopulmonary resuscitation quality and beyond: the need to improve real-time feedback and physiologic monitoring. Critical Care 2016;20:182. [Crossref] [PubMed]
7. Ruiz J, De Gauna SR, Bahillo P, et al., editors. Estimation of Chest Compression Rate and Detection of Hands-off Intervals During Resuscitation With Automated External Defibrillators. computing in cardiology conference; 2018.
8. Ristagno G. Transthoracic impedance waveform during cardiopulmonary resuscitation: One size does not fit all! Resuscitation 2014;85:579-80. [Crossref] [PubMed]
9. Aramendi E, Ayala U, Irusta U, et al. Suppression of the cardiopulmonary resuscitation artefacts using the instantaneous chest compression rate extracted from the thoracic impedance. Resuscitation 2012;83:692-8. [Crossref] [PubMed]
10. González-Otero DM, Sofía RDG, Ruiz J, et al. Chest compression rate feedback based on transthoracic impedance. Resuscitation 2015;93:82-8. [Crossref] [PubMed]
11. Zhang H, Yang Z, Huang Z, et al. Transthoracic impedance for the monitoring of quality of manual chest compression during cardiopulmonary resuscitation. Resuscitation 2012;83:1281-6. [Crossref] [PubMed]
12. Alonso E, Gonzalezotero DM, Aramendi E, et al. Can thoracic impedance monitor the depth of chest compressions during out-of-hospital cardiopulmonary resuscitation? Resuscitation 2014;85:637-43. [Crossref] [PubMed]
13. Lin S, Turgulov A, Taher A, et al. Automated Data Abstraction of Cardiopulmonary Resuscitation Process Measures for Complete Episodes of Cardiac Arrest Resuscitation. Acad Emerg Med 2016;23:1178-81. [Crossref] [PubMed]
14. Stecher FS, Olsen J, Stickney RE, et al. Transthoracic4impedance used to evaluate performance of cardiopulmonary resuscitation during out of hospital cardiac arrest. Resuscitation 2008;79:432-7. [Crossref] [PubMed]
15. Berve PO, Irusta U, Kramer-Johansen J, et al. Transthoracic Impedance Measured with Defibrillator Pads-New Interpretations of Signal Change Induced by Ventilations. J Clin Med 2019;8:724. [Crossref] [PubMed]
16. Risdal M, Aase SO, Stavland M, et al. Impedance-based ventilation detection during cardiopulmonary resuscitation. IEEE Trans Biomed Eng 2007;54:2237-45. [Crossref] [PubMed]
17. Ayala U, Eftestøl T, Alonso E, et al. Automatic detection of chest compressions for the assessment of CPR-quality parameters. Resuscitation 2014;85:957-63. [Crossref] [PubMed]
18. Alonso E, Ruiz J, Aramendi E, et al. Reliability and accuracy of the thoracic impedance signal for measuring cardiopulmonary resuscitation quality metrics. Resuscitation 2015;88:28-34. [Crossref] [PubMed]
19. Risdal M, Aase SO, Stavland M, et al. Impedance-based ventilation detection during cardiopulmonary resuscitation. IEEE Trans Biomed Eng 2007;54:2237-45. [Crossref] [PubMed]
20. Xiang D. Automatic detection algorithm for chest compressions signal with classification algorithm. Adv Mat Res 2014;926-930:3493-6. [Crossref]
21. Dunn JC. A fuzzy relative of the SODATA process and its use in detecting compact well-separated cluster. J Cybemet 1974;3:32-57.
22. Bezdek JC, Dunn JC. Optimal fuzzy partitions: a heuristic for estimating the parameters in a mixture of normal distributions. IEEE Trans Comput 1975;C-24:835-8. [Crossref]
23. Nayak J, Naik B, Behera HS. Fuzzy C-means (FCM) clustering algorithm: a decade review from 2000 to 2014. Computational Intelligence in Data Mining. New Delhi, India: Springer; 2015.
24. Javadi S, Rameez M, Dahl M, et al. Vehicle classification based on multiple fuzzy c-means clustering using dimensions and speed features. Procedia Computer Science 2018;126:1344-50. [Crossref]
25. Haldar NAH, Khan FA, Ali A, et al. Arrhythmia classification using Mahalanobis distance based improved Fuzzy C-Means clustering for mobile health monitoring systems. Neurocomputing 2017;220:221-35. [Crossref]
26. Zhao Z, Jiao L, Zhao J, et al. Discriminant deep belief network for high-resolution SAR image classification. Pattern Recognition 2017;61:686-701. [Crossref]
27. Huang C, Gong W, Fu W, et al. A research of speech emotion recognition based on deep belief network and SVM. Mathematical Problems in Engineering 20144. [Crossref]
28. Al-Fatlawi AH, Jabardi MH, Ling SH, editors. Efficient diagnosis system for Parkinson's disease using deep belief network. 2016 IEEE Congress on Evolutionary Computation (CEC); 2016. doi: [Crossref]
29. Meaney PA, Bobrow BJ, Mancini ME, et al. Cardiopulmonary resuscitation quality: improving cardiac resuscitation outcomes both inside and outside the hospital: a consensus statement from the American Heart Association. Circulation 2013;128:417-35. [Crossref] [PubMed]
30. Weichert V, Sellmann T, Wetzchewald D, et al. Two minutes CPR versus five cycles CPR prior to reanalysis of the cardiac rhythm: A prospective, randomized simulator-based trial. Resuscitation 2015;96:142-7. [Crossref] [PubMed]
31. Ruiz J, Ayala U, de Gauna SR, et al. Feasibility of automated rhythm assessment in chest compression pauses during cardiopulmonary resuscitation. Resuscitation 2013;84:1223-8. [Crossref] [PubMed]
32. Jalali A, Berg RA, Nadkarni VM, et al. Mathematical Modeling of Cardiopulmonary Resuscitation. 2015. doi: 10.1115/DSCC2015-9978. [Crossref]
33. Silva Filho TM, Pimentel BA, Souza RMCR, et al. Hybrid methods for fuzzy clustering based on fuzzy c-means and improved particle swarm optimization. Expert Syst Appl 2015;42:6315-28. [Crossref]
34. Ling Z, Deng L, Yu D. Modeling spectral envelopes using restricted boltzmann machines and deep belief networks for statistical parametric speech synthesis. IEEE T Audio Speech 2013;21:2129-39. [Crossref]
35. Smolensky P. Information processing in dynamical systems: Foundations of harmony theory. In: Rumelhart DE, McClelland JL, editors. Parallel Distributed Processing. Cambridge: MIT Press; 1986:194-281.

(English Language Editor: A. Kassem)