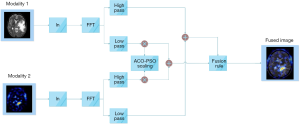
Application of hybrid particle swarm and ant colony optimization algorithms to obtain the optimum homomorphic wavelet image fusion

The medical image fusion methods illustrate beneficial aspects to enhance the clinical assessment to give satisfying biomedical data. The multimodal fused images supply prosperous diagnosis abilities in medical cases compared to the single image. The multimodal clinical image fusion is a procedure in which different fusion methods are combined to enhance the capability of the image processing in the clinical evaluations. On the recent papers on the image merging process, multimodal image fusion plays a vital role in information fusion. In this regard, the decompositions, according to the multi-scale procedure, are mostly conducted applying transformation functions. Bhateja et al. (1) presented a hybrid method on the Contourlet and wavelet functions for medical image fusion aims where a multi-stage fusion approach is carried out for MRI and CT scan images fusion. For the clinical image, merging aims, a practical, functional mapping, along with an efficient structural mapping, is an essential element. There have been proposed different techniques for medical image fusion in various literature in recent few years. For instance, Srivastava et al. (2) presented the image fusion by the aim of the curvelet method, where the Curvelet techniques present much more structural properties. In another work, Bhateja (3) suggested the NSCT (non-subsampled contourlet transform) method for image fusing of the medical images, where the complementary modalities high and low frequencies are merged according to the single fusion principles. Newly presented image fusion methods, namely decomposition framework on the moving frames, are intended to image local geometry.

For example, Chen et al. (4) developed moving frames for keeping the local geometry in image processing. Liu et al. (5) presented a novel approach called non-subsampled shearlet transform (NSST) method, where more edges and text data can be shifted from the primary images into the final fused images. In recent years, methods on the hybridized fuzzy Contourlet were employed to the fusion of the multi-level clinical images, where the high frequency of the contourlet domain and approximation properties have been fused applying according to the fuzzy techniques (6). Du et al. (7) presented a decomposition method on the Laplacian filtering for multimodal image fusion. Yang et al. (8) fused the multi-level MR-CT, MR-SPECT, and MR-PET images with the non-subsampled contourlet fuzzy logic technique. Wang et al. (9) applied a novel method, namely SIST (shift-invariant shearlet transform), shaped with the Gaussian density function for the multimodal image fusion. The methods for the Wavelet decomposition play a vital role in the multi-level image fusion (10).

For more literature reviews, the quaternion wavelet transform (QWT) is proposed by Chai et al. (11), where the intended method is applied for the medical images, infrared-visible images, multi-focus images, and remote-sensing images. Discrete fractional wavelet transform (DRWT) method can give multimodal time-fractional frequency zone properties of the purposed image (12). Zhu et al. proposed a novel dictionary-learning method for multimodal image fusion. Their suggested method forms three stages. The first step is image sample patching; the second step is the clustering algorithm for classification of the patches of the images, and the third step is combining the sub-dictionaries for the creation of a comprehensive dictionary. In the produced dictionary, only the essential data which describe the images efficiently are chosen (13). Chen et al. (14) recommended a novel technique according to the intensity-hue-saturation (IHS) model, and log-Gabor wavelet transforms to assist the doctor for a better detection by the aim of rendering the anatomical structures. Du et al. (15) proposed an advantageous technique for anatomical and functional images fusion in which the merging of the images performed within combining the parallel saliency properties in the multimodal domain. A novel method for multi-level image fusion has been presented by Chavan et al. (16). Their proposed method is applied for lesion evaluation in diagnosing process and Neurocysticercosis analysis. The presented Multimodality Medical Image Fusion is a novel method for the fusion of CT and MRI images of a patient by the aim of the NSRCxWT transform technique. In the last few years, different computational methods have been employed for combining the multimodal images. Kavitha et al. (17) proposed a novel hybrid method for multimodality image fusion. Their proposed algorithm is an integration of ant colony optimizer and a pulse-coupled neural network for enhanced image fusion aims. Xu et al. (18) presented an integrated method, including a pulse-coupled neural network, coupled with quantum-behaved particle swarm optimization for image fusion aims.

Besides the presented methods, there are different literature focusing on image fusion with soft computational techniques. Liu et al. (19) employed convolutional neural network (CNN), Human Visual System (HVS) inspired method applied by Bhatnagar et al. (20), the fuzzy-adaptive RPCNN (reduced pulse-coupled neural network) employed by Das et al. (21), hybrid grey wolf and cuckoo search-based model (22), grey wolf optimizer (23).

Furthermore, there are many applications intelligent-based image fusion, including tumor diagnosis, brain surgery, treatment of the Alzheimer’s, and other medical applications (24-30).

In the present work, the greatest homomorphic filtration creates multi-level decomposition. For obtaining the best image fusion, a hybrid method which is an integration of particle swarm optimizer (PSO) and ACO algorithms. We present the following article in accordance with the MDAR reporting checklist (available at http://dx.doi.org/10.21037/atm-20-5997).

The sections of the paper organized as the following order:

• Part 2 is that the filtrating method is comprehensively described.
• Part 3 presents the proposed hybrid optimization.
• Part 4 discusses the results.

Methods

This part of the paper implemented the proposed homomorphic filtering method to enhance the image’s brightness as well as its contrast. The Butterworth filter that is a high-pass filter is used for sharpening purposes for improvement of the picture.

Homomorphic filtering method

As depicted in Figure 1, the conventional filtering procedure of the homomorphic filtering contains the ln (denoting the logarithmic transforming), fast Fourier transform (FFT), filter H(u,v), Inverse FFT (IFFT). Finally, the exponential transform (exp) is applied. As depicted in the below formula, each picture is the production of the illumination (z₁(x,y)) and reflectance (z₂(x,y)) (31):

Figure 1 Schematic of generalized homomorphic method of filtering.

z(x,y) = z₁(x,y) * z₂(x,y) [1]

The low-frequency constituents and horizontal sections in the frequency and spatial domains are related to the illumination. Whereas, the high-frequency components, as well as the indicate edge, details, and noises, are related to the reflectance. This paper employed ln to divide the illumination from reflectance as follows:

z(x,y) = ln(z₁(x,y)) + ln(z₂(x,y)) [2]

This study also implemented FFT on Eq. [2] as:

Z(u,v) = Z₁(u,v) + Z₂(u,v) [3]

Following that, the homomorphic filtering is applied as follows:

S(u,v) = H(u,v)Z(u,v) = H(u,v)Z₁(u,v) + H(u,v)Z₂(u,v) [4]

It is possible to improve the illumination and reflectance constituents in various manners by choosing a proper filter. Thus, the homomorphic filtering is an important task. The main aim of the filtering is to improve the picture details (repression of the low-frequency sections and amplification of the high-frequency sections). Therefore, it must use a high-pass filter to sharpen an image.

After the stated steps, inverse FFT and exp operators are applied to the filtered constituents as:

s(x,y) = F^−1[S(u,v)] = F^−1[H(u,v)Z₁(u,v)] + F^−1[H(u,v)Z₂(u,v)] = s₁(x,y) + s₂(x,y) [5]

And the final filtered image can be presented by:

g(x,y) = exp s(x,y) = exp [s₁(x,y) + s₂(x,y)] = exp s₁(x,y) * exp s₂(x,y) = s_1,0(x,y) * s_2,0(x,y) [6]

As can be seen, the final image composed of illumination and reflection terms being the low and high-frequency parts, respectively.

Presented greatest homomorphic filter

The proposed homomorphic filtering method is the best multi-level scaling technique, where the multi-scale decomposition is conducted on the wavelet transform. The procedure for the proposed method is illustrated in Figure 2. The input image includes illumination and reflection constant values, as presented in Eq. [1] mapped to the logarithmic domain, and the output picture is conferred in Eq. [2]. The resultant image of the logarithmic domain is mapped to the wavelet domain.

Figure 2 Schematic of presented homomorphic method of filtering on wavelet transform.

$$\{\begin{array}{c}{W}_{1\mathrm{ϕ}}\left(j_0,m,n\right)=\frac{1}{\sqrt{MN}}\underset{x=0}{\overset{M−1}{{\displaystyle ∑}}}\underset{y=0}{\overset{N−1}{{\displaystyle ∑}}}z\left(x,y\right)\mathrm{ϕ}\left(j_0,x,y\right)\\ W_{1\mathrm{ψ}}^i\left(j_0,m,n\right)=\frac{1}{\sqrt{MN}}\underset{x=0}{\overset{M−1}{{\displaystyle ∑}}}\underset{y=0}{\overset{N−1}{{\displaystyle ∑}}}z\left(x,y\right){\mathrm{ψ}}^i\left(j_0,x,y\right)\end{array}$$[7]

$$\{\begin{array}{c}{W}_{2\mathrm{ϕ}}\left(j_0,m,n\right)=\frac{1}{\sqrt{MN}}\underset{x=0}{\overset{M−1}{{\displaystyle ∑}}}\underset{y=0}{\overset{N−1}{{\displaystyle ∑}}}z\left(x ,y\right)\mathrm{ϕ}\left(j_0,x,y\right)\\ W_{2\mathrm{ψ}}^i\left(j_0,m,n\right)=\frac{1}{\sqrt{MN}}\underset{x=0}{\overset{M−1}{{\displaystyle ∑}}}\underset{y=0}{\overset{N−1}{{\displaystyle ∑}}}z\left(x ,y\right){\mathrm{ψ}}^i\left(j_0,x,y\right)\end{array}$$[8]

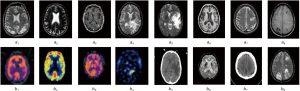
The modalities one and two decomposed high and low pass filtered properties are presented in Figures 3 and 4, in which i={H,V,D} indicates the input modality horizontal, vertical, and diagonal features.

Figure 3 The required input data sets MR-SPECT(a₁, a₂, b₁, b₂), MR-PET(a₃, a₄, b₃, b₄), MR-CT(a₅, a₇, b₅, b₇), and MR-T1-T2(a₆, a₈, b₆, b₈). MR-SPECT, magnetic resonance spectroscopy; MR-PET, magnetic resonance positron emission tomography; MR-CT, magnetic resonance computed tomography; MR-T1-T2, magnetic resonance-transform 1-transform 2.

Figure 4 Fused images (A) DCT, (B) DWT, (C) FFT, (D) IHS, (E) OWMF-GA, (F) presented method. DCT, discrete computed tomography; DWT, discrete wavelet transform; FFT, fast fourier transform; HIS, intensity-hue-saturation; OWMF-GA, optimum wavelet-based homomorphic-genetic algorithm.

$$z_1\left(u,v\right)=W_{2\mathrm{ϕ}}\left(j_0,m,n\right)+W_{1\mathrm{ψ}}^i\left(j,m,n\right)$$[9]

$$z_2\left(u,v\right)={\mathrm{σ}}_1{W}_{\mathrm{ϕ}}\left(j_0,m,n\right)+{\mathrm{σ}}_2{W}_{\mathrm{ψ}}^i\left(j,m,n\right)$$[10]

Herein, the output of the adder 1 and 2 are represented by z₁(u,v) and z₂(u,v), respectively.

z_fused = Average(z₁(u,v), z₂(u,v))[11]

z(x,y)=W^−1(z(u,v))[12]

g(x,y)=exp(z(x,y))[13]

Therein, z(u,v) denotes the resultant of the fused wavelet homomorphic, as presented in Eq. [11]. Besides, g(x,y) stands for the fused image in the spatial domain on Eq. [13].

The proposed hybrid optimization method

PSO algorithm

The PSO is an evolutionary method, suggested in (32) for the first time. This method is inspired by the treatment of the birds’ swarm. This algorithm creates some probable answers randomly. Then, these solutions will be enhanced until achieving the best solution for the problem. Each of the individuals in the PSO population has a location and velocity. This algorithm records the best-obtained solution of everyone (pbest) and the best solution of all individuals (gbest). These greatest solutions affect the movement of individuals (33). The best solution achieves in this algorithm by an objective function (OF). The PSO updates the velocity of everyone by:

V_new = w*V_old+c₁*r₁*(pbest−P_old )+c₂*r₂*(gbest−P_old)[14]

Where, P_old and V_old denote the location and velocity of the individual for the prior iterative step; V_new indicates the computed velocity of the current step; c₁ and c₂ signify the training parameters both in the range of 0–1. Also, r₁ and r₂ are two randomly generated numbers at the interval of 0–1. These two random numbers are generated for keeping the velocity in an allowable range. Moreover, w shows the weight (inertia parameter). Subsequently, the new location of every one is obtained as:

P_new = V_new + P_old[15]

This process will be continued until satisfying the end condition. This algorithm is presented step-by-step in the below:

• Initializing the location/velocity of everyone by random.
• Iteration.
• Computing the pbest and gbest.
• Updating the velocities and locations of the individuals using Eq. [14] and relation Eq. [15], respectively.
• The optimization procedure is over by satisfying the end condition.
• The best solution is the obtained global best.

ACO algorithm

Each of the ants records the OF value (its obtained the best location) (34). Two criteria are considered, including a distance criterion and a probability one, which are presented in Eq. [16]. Each of the ants moves to rely on these two metrics and updates the amount of the deposited pheromone on its covered path using Eq. [17]. This algorithm continues until converging all ants to an identical path.

$$p_{ij}\left(t\right)=\frac{{\left[{\mathrm{Ï„}}_{ij}\left(t\right)\right]}^{\mathrm{Î\pm }}{\left[{\mathrm{η}}_{ij}\left(t\right)\right]}^{\mathrm{β}}}{{{\displaystyle ∑}}_{j∈N_i}\left({\left[{\mathrm{Ï„}}_{ij}\left(t\right)\right]}^{\mathrm{Î\pm }}{\left[{\mathrm{η}}_{ij}\left(t\right)\right]}^{\mathrm{β}}\right)}$$[16]

In which, p_ij(t) denotes the probability of ant selecting the path of i^th to j^th node; Ï„_ij indicates the concentration of the pheromone in the edge among i^th and j^th nodes, and:

$${\mathrm{η}}_{ij}\left(t\right)=\frac{1}{d_{ij}}$$[17]

In which, d_ij shows the distance of i^th to the j^th node. Also, α and β signify the decay parameters that presented the pheromone’s fading value by the time. Value of the pheromone will be computed in each step by:

τ_ij(t+1) = τ(t)*(1−ρ)+Δτ_ij(t)[18]

In this equation, ρ denotes the ratio of the pheromone decay, which takes value in the range of 0–1. As well, Δτ_ij(t) is the furthered pheromone deposited on the t^th the time interval that can be computed as follows:

Δτ_ij(t) = ∑τ_ij(k) for 1≤k≤m[19]

The ant colony optimizer has the main drawback, which is the probability of converging to the local best answer. Steps of this algorithm are presented as follows:

• Initializing the ants’ locations and pheromone values.
• Iterating for each ant.
• Structuring the distance index, which is based on the flow data and length of the path.
• Structuring the probability index based on the Eq. [16].
• Employing the local exploration for movement deciding of the ants based on two introduced metrics.
• Updating the concentration of the pheromone using Eq. [18].
• Continue until reaching the end term or edge router.

Combined PSO-ACO optimizer

These results suggested the hybrid method unifies the ACO and PSO algorithms, which are on the distance and velocity, respectively. This novel hybrid method promotes the efficiency of the Ant Colony optimizer. The PSO and ACO algorithms have a common drawback trapping in the local best solution. The reason behind this drawback is the unreal initialization of the pheromone concentration and individuals’ distance in the Ant Colony and Particle Swarm Optimizers, respectively. In the Ant Colony method, movements are decided on the prior greatest movements of ants. In the proposed hybrid, locations of the ants are updated on the local and globally best solutions, which leads to more velocity and accuracy. As well, this proposed method achieved the greatest solution with a lower count of the ants. So, it can be claimed that this hybrid method reduces the computing burden comparatively with the standard ACO method. Local visibility of k^th ant for achieving the target placed in (i,j) is represented by:

$${\mathrm{η}}_{ij}^k\left(t\right)=\frac{{\text{Ω}}^k}{d_{is}^k\left(t\right)}$$[20]

The obtained value must be lower than 1, and once it is higher than one, it should be adjusted to 1. In this relation, Ω^k denotes the local detection parameter on the flow data. ^{Also^}$d_{is}^k\left(t\right)$^{shows the distance ofkth ant and the attack} resource. High visibility of the target denotes the ant is close to the attack source. So, the ant movement is on this parameter. It moves by the updated velocity/location. In the proposed hybrid optimizer, the velocity of everyone is computed by Eq. [21]. After that, updated their locations Eq. [22]. In this process, three weight parameters (Ψ_e,Ψ_c and Ψ_s) are used to compute the individual’s velocity. The first factor (Ψ_e) is the explorative parameter that assists the ant to collect information from the environment; Ψ_c denotes the cognitive parameter and its value relies on the obtained pbest points; Ψ_s indicates the social parameter, and its value relies on the obtained gbest solution.

$$V_{i,d}^k\left(t+1\right)={\text{Ψ}}_e*r_e*V_{i,d}^k\left(t\right)+{\text{Ψ}}_c*r_c*\left[P_c−P_{i,d}^k\left(t\right)\right]+{\text{Ψ}}_s*r_s*\left[P_s−P_{i,d}^k\left(t\right)\right]$$[21]

Then, a new location can be computed by:

$$P_{i,d}^k\left(t+1\right)=P_{i,d}^k\left(t\right)+V_{i,d}^k\left(t+1\right)$$[22]

In these equations, P_c is the pbest point, while P_s denotes ^{thegbest solution;}$P_{i,d}^k\left(t\right)$^{is the location of}k^{th ant at time}t on (i,d) edge and V_i,d(t) denotes its velocity. Also, r_e,r_c and r_s are three haphazard values in the range of 0-1. Use of ant colony optimizer is provided in Eqs. [23-24] in the proposed optimization procedure, where the pheromone concentration is computed by:

$$J_{ij}^k\left(t+1\right)=\mathrm{ρ}\left[J_{ij}^k\left(t\right)+T_{ij}^k\right]−\left(1−\mathrm{ρ}\right)*e*J_{ij}^k\left(t\right)$$[23]

In which, ρ takes value in the range of 0–1, and e denotes the elimination factor presenting the decay of the pheromone concentration by the time. Its value is supported lower than one, in a way that, decaying the pheromone be slower than its deposition by the ants. The ants whom they are not sourced agents only distribute the pheromone, which reached from the source one. In the above relations, $T_{ij}^k$ denotes the pheromone concentration obtained from adjacent ants, and it can be presented by:

$$T_{ij}=\{\begin{array}{c}\mathrm{Î\pm }      for source pheromone\\ \mathrm{β}     for other ones\end{array},0<\mathrm{β}<\mathrm{Î\pm }<1$$[24]

A source ant is defined as an agent, who can find the path with no aid of the adjacent ants. Also, the source pheromone is the distributed pheromone of a source ant. The target utility can be computed by:

$${\mathrm{μ}}_{ij}^k\left(t\right)=\frac{k_1*W_{ij}^k\left(t\right)−k_2*J_{ij}^k\left(t\right)}{R}$$[25]

Where $W_{ij}^k\left(t\right)$ is the path weight, and $J_{ij}^k\left(t\right)$ is the pheromone concentration. Value of $W_{ij}^k\left(t\right)$ relies on the flow data as an indicator for the count of attack packets over the path. Also, R denotes the local redundancy parameter showing the count of the adjacent agents that refer to the equal path. Moreover, k₁,k₂ are the two coefficients. Agents of ant colony optimizer tend to select the paths with higher target utility, which results in converging to a local greatest point. The proposed hybrid algorithm tackles this problem. The suggested PSO-ACO optimizer is represented in Algorithm 1.

Results

Source images

The efficiency of the suggested fusion method is investigated in the present part of the paper. These results suggested the fusion method is applied to different input modalities, including MR-SPECT, MR-PET, and MR-CT modalities, as well as MR-T1-T2 one. The utilized dataset of images is taken from http://www.med.harvard.dedu/AANLIB/home.html.

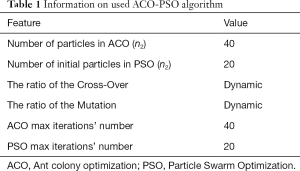
Information on the used ACO-PSO algorithm is listed in Table 1. The obtained best scales by the proposed ACO-PSO hybrid algorithm are presented in Table 2. In this table, σ₁ and σ₂ are the best values related to modalities 1 and 2. The simulations are carried out on MATLAB.

Table 1 Information on used ACO-PSO algorithm
Full table

Table 2 Obtained best scale values by hybrid ACO-PSO algorithm
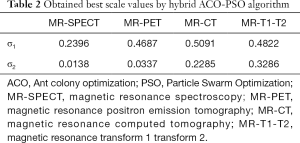
Full table

Objective assessment metrics

It’s relatively a hard task to assess the quality of the fused images using quantitative metrics. The main reason behind this hardness is that there is no practical reference image. Many fusion indices are suggested recently in the literature. However, none of these metrics is proved globally to be always more reliable compared with other ones in different fusion cases. So, it’s essential to considered multitude indices achieving a reliable assessment. In the present work, several indices are considered for quantitative analysis of the proposed method including edge quality (Q^AB/F) and entropy (E) (35) as well as MI (denoting the mutual-information) (36) and SD (standard deviation) (37). Let A and B indicate two source images, whereas, F denotes the fused image.

Edge quality

The edge quality is a popular fusion criterion that computes the amount of gradient information injected to the fused image from the source one. This metric is comprehensively defined in (35).

Entropy

This metric can be computed by:

$$E=−\underset{l=0}{\overset{L−1}{{\displaystyle ∑}}}{p}_F\left(l\right){\log }_2{p}_F\left(l\right)$$ [26]

In which, L denotes the number of gray level, and p_F(l) indicates the normalized histogram of the fused image. Entropy is employed for measuring the amount of information in a fused image.

Mutual information

This metric can be defined as:

MI=H(I₁)+H(I₂)−H(I₁,I₂) [27]

In which, I₁ and I₂ are the reference and sensed images, respectively; H(I₁) is the entropy value of I₁; H(I₂) indicates the entropy value of I₂; H(I₁,I₂) signifies the entropy of the joint probability distribution of the images intensities.

H(I₁)=−∑ip₁(i)log₂p₁(i) [28]

H(I₂)=−∑ip₂(i)log₂p₂(i) [29]

H(I₁,I₂)=−∑(i,j)p₁₂(i,j)log₂p₁₂(i,j) [30]

Where, p₁ and p₂ denote probability densities. Also, p₁₂ indicates the joint probability density.

Statistical intensities of images, as well as their joint probability distribution, are considered in MI metric. So, this metric can guarantee that the max level is achieved once two images are matched.

Standard deviation

This metric can be computed by:

$$SD=\sqrt{\frac{1}{HW}\underset{x=1}{\overset{H}{{\displaystyle ∑}}}\underset{y=1}{\overset{W}{{\displaystyle ∑}}}{\left[F\left(x,y\right)−\mathrm{μ}\right]}^2}$$ [31]

In this formula, μ denotes the average value of the fused image. This metric measures the total contrast of the fused image.

Additionally, a comparison is performed between the suggested method and different well-known methods, including DCT (38), DWT (39), FFT (40), and HIS (41). As well, the proposed optimization is compared with some famous optimizers like Genetic Algorithm and Particle Swarm Optimization. Instances of two input image modalities are represented in Figure 3.

Moreover, four different modalities including MR-SPECT, MR-PET, and MR-CT, and MR-T1-T2 modalities are employed to show advantages of the suggested fusion method. Firstly, efficiency of the proposed method based on the hybrid PSO-ACO algorithm is verified using the mentioned objective fusion metrics. Following that, an overall comparison is made regarding considered objective metrics.

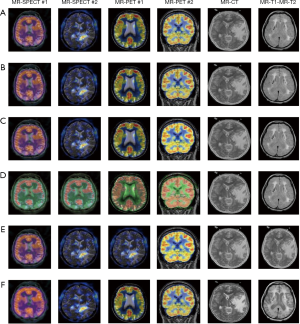
MR-SPECT cases

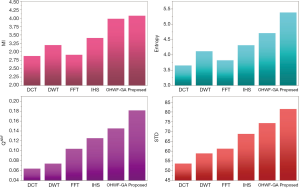
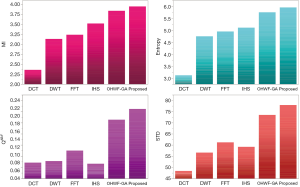
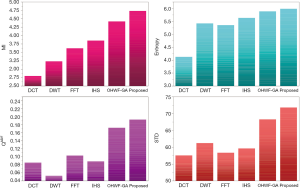
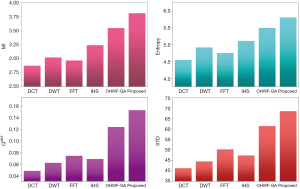
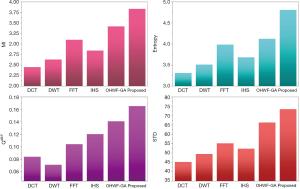
The fusion results of SPECT-MRI are illustrated in Figure 4. In Figure 4, first and second columns are the fused images of SPECT-MRI our proposed method. As can be seen, metabolic data of SPECT images is mapped on the anatomy characteristics of MRI images. Figures 5 and 6 illustrate the obtained results for datasets 1 and 2 of MR-SPECT images, respectively. On the presented results in Table 2, the suggested method could overtake other methods in the considered metrics. Also, the evaluation indices of proposed and comparing methods are demonstrated in Figures 5 and 6. These figures show our suggested fusion method has the best performance on all the image fusion metrics, including MI, Entropy, Q^AB/F, and STD. Therefore, as our stated approach presents more excellent performance on both subjective visual and objective metrics, it can designate our proposed technique outperforms conventional methods.

Figure 5 The obtained results for the fusion of MR-SPECT case #1 images. MR-SPECT, magnetic resonance spectroscopy.

Figure 6 The obtained results for the fusion of MR-SPECT case #2 images. MR-SPECT, magnetic resonance spectroscopy.

MR-PET cases

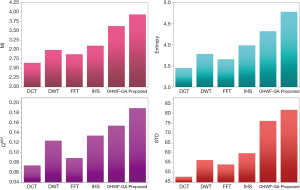
MRI–PET is a new imaging modality that links anatomic and metabolic data acquisition. The MRI image can give a clear soft-tissue image, and the PET image can create a 3D image of tracer concentration within the body. The benefits of MRI–PET fusion are registration of the two modalities that cannot only largely replace PET-only scanners in clinical routine, but also expand the clinical and research roles considerably. The suggested method is used here for the fusion of the MR images with PET images, and obtained results are illustrated in Figure 4 for datasets 3 and 4. Also, the obtained results are compared in Figures 7 and 8 for various methods in terms of the considered metrics. It can be seen obviously that the suggested technique outperforms other methods in MI results in Figures 7 and 8. MI is a matching measure of the visual image quality. In that case, on the visualization, the proposed method is better than the rivals. Also, the proposed method is leading in the Entropy and STD metrics. Besides, the suggested multi-modal medical image fusion method illustrates better performance than the traditional approaches in terms of Q^AB/F. Briefly, the recommended method performs superior compared to other common techniques.

Figure 7 The obtained results for the fusion of MR-PET case #1 images. MR-PET, magnetic resonance positron emission tomography.

Figure 8 The obtained results for the fusion of MR-PET case #2 images. MR-PET, magnetic resonance positron emission tomography.

MR-CT and MR-T1-T2 cases

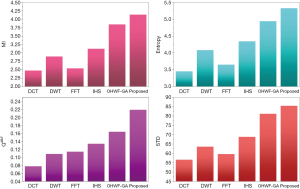
Two other modalities (CT and T1–T2) are also fused with MR images using the suggested method. In this subsection, MR soft tissues are fused with CT pictures. While both soft and hard tissues, data can be mapped to a single frame. The obtained metrics for various methods are depicted in Figures 9-12. As can be seen from these results, our suggested method led to higher performance compared with other well-known methods. As well, the fusion results for both modalities are depicted in Figure 4.

Figure 9 The obtained results for the fusion of MR-CT case #1 images. MR-CT, magnetic resonance computed tomography.

Figure 10 The obtained results for the fusion of MR-CT case #2 images. MR-CT, magnetic resonance computed tomography.

Figure 11 The obtained results for the fusion of MR-T1-T2 case #1 images. MR-T1-T2, magnetic resonance-transform 1-transform 2.

Figure 12 The obtained results for the fusion of MR-T1-T2 case #2 images. MR-T1-T2, magnetic resonance-transform 1-transform 2.

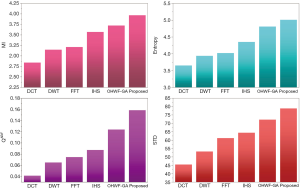
Our suggested OWHF method on the hybrid ACO-PSO algorithm could overtake other well-known methods in various cases. Moreover, a higher number of anatomic/metabolic characteristics are mapped to a single image using our suggested method. Using hybrid ACO-PSO algorithms can also be considered our second novelty of this work, which could present a dynamic range for scale values.

Discussion

Medical imaging is an important issue in medicine due to its great impact and sensitivity on diagnosing various medical issues. Recently, medical image fusion has appeared as an effective method in merging the medical images of different modalities. Indeed, the fused image helps the physician in disease diagnosis for efficient treatment planning. The fusion process combines multi-modal images to incur a single image with excellent quality, retaining original images' information. The fusion algorithm is an aid to radiologists for better visualization, accurate interpretation, and precise localization of the lesions formed in the brain. In the present work, a novel method, namely the optimum homomorphic wavelet fusion (OHWF) technique, is proposed to fuse the multimodal clinical images. In the present work, a novel method, namely the OHWF technique, to fuse the multimodal clinical images. The technique gathered both advantages of the wavelet decomposition method and the homomorphic filter in a single configuration. The benefits of homomorphic filtering and wavelet transformation in the image fusion process are highlighted. The suggested scheme increases the quality of the fusion of the medical images through the combination of the functional and anatomical characteristics applying multi-level decomposition. The proposed fusion technique is authenticated, using different fusion assessment metrics for MR-PET, MR-SPECT, MR-T1-T2, and MR-CT image fusions.The suggested scheme increases the quality of the fusion of the medical images through the combination of the functional and anatomical characteristics applying multi-level decomposition. The proposed fusion technique is authenticated, applying different fusion assessment metrics for MR-PET, MR-SPECT, MR-T1-T2, and MR-CT image fusions. The best image fusion values are obtained utilizing hybrid ant colony and particle swarm algorithms (hybrid ACO-PSO).

To improve the fusion efficiency, a new hybrid optimization algorithm called the hybrid ACO-PSO is presented and applied to the wavelet system for optimal decomposition. To show the system efficiency, the simulation results are analyzed by comparing with different medical image fusion methods based on different measures, including MI, Q^AB/F, STD, and Entropy values. The obtained results illustrated that the employed technique for image fusion overweights the other well-known methods in the fusion results. Moreover, a higher number of anatomic/metabolic characteristics are mapped to a single image using the suggested method.

For analyzing the efficiency of the hybrid optimization method, the ACO-PSO hybrid method is compared to different image fusing methods by considering different performance criteria, including information, edge quality, entropy, and standard deviation. The obtained results illustrated that the employed technique for image fusion overweights the other well-known methods in the fusion results. In the clinical diagnosis, the fusion methods, likewise, the multi-level decomposition approach, plays an important role which was obtained within the proposed method.

Acknowledgments

We thank Guangzhou Yujia Biotechnology Co., Ltd for helpful conversations.

Funding: None.

Footnote

Reporting Checklist: The authors have completed the MDAR reporting checklist. Available at http://dx.doi.org/10.21037/atm-20-5997

Data Sharing Statement: Available at http://dx.doi.org/10.21037/atm-20-5997

Conflicts of Interest: Both authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/atm-20-5997). The authors have no conflicts of interest to declare.

Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.

References

1. Bhateja V, Patel H, Krishn A, et al. Multimodal medical image sensor fusion framework using cascade of wavelet and contourlet transform domains. IEEE Sensors Journal. 2015;15:6783-90. [Crossref]
2. Srivastava R, Prakash O, Khare A. Local energy-based multimodal medical image fusion in curvelet domain. IET Computer Vision 2016;10:513-27. [Crossref]
3. Bhateja V, Moin A, Srivastava A, et al. Multispectral medical image fusion in Contourlet domain for computer based diagnosis of Alzheimer’s disease. Rev Sci Instrum 2016;87:074303. [Crossref] [PubMed]
4. Chen Y, Liu J, Hu Y, et al. Discriminative feature representation: an effective postprocessing solution to low dose CT imaging. Phys Med Biol 2017;62:2103. [Crossref] [PubMed]
5. Liu X, Mei W, Du H. Multi-modality medical image fusion based on image decomposition framework and nonsubsampled shearlet transform. Biomed Signal Process Control 2018;40:343-50. [Crossref]
6. Darwish SM. Multi-level fuzzy contourlet-based image fusion for medical applications. IET Image Processing 2013;7:694-700. [Crossref]
7. Du J, Li W, Xiao B, et al. Union Laplacian pyramid with multiple features for medical image fusion. Neurocomputing 2016;194:326-39. [Crossref]
8. Yang Y, Que Y, Huang S, et al. Multimodal sensor medical image fusion based on type-2 fuzzy logic in NSCT domain. IEEE Sensors Journal 2016;16:3735-45. [Crossref]
9. Wang L, Li B, Tian LF. EGGDD: An explicit dependency model for multi-modal medical image fusion in shift-invariant shearlet transform domain. Information Fusion 2014;19:29-37. [Crossref]
10. Lifeng Y, Donglin Z, Weidong W, et al. Multi-modality medical image fusion based on wavelet analysis and quality evaluation. Journal of Systems Engineering and Electronics 2001;12:42-8.
11. Chai P, Luo X, Zhang Z. Image fusion using quaternion wavelet transform and multiple features. IEEE Access 2017;5:6724-34.
12. Xu X, Wang Y, Chen S. Medical image fusion using discrete fractional wavelet transform. Biomed Signal Process Control 2016;27:103-11. [Crossref]
13. Zhu Z, Chai Y, Yin H, et al. A novel dictionary learning approach for multi-modality medical image fusion. Neurocomputing 2016;214:471-82. [Crossref]
14. Chen CI. Fusion of PET and MR brain images based on IHS and log-Gabor transforms. IEEE Sensors Journal 2017;17:6995-7010. [Crossref]
15. Du J, Li W, Xiao B. Fusion of anatomical and functional images using parallel saliency features. Information Sciences 2018;430:567-76. [Crossref]
16. Chavan SS, Mahajan A, Talbar SN, et al. Nonsubsampled rotated complex wavelet transform (NSRCxWT) for medical image fusion related to clinical aspects in neurocysticercosis. Comput Biol Med 2017;81:64-78. [Crossref] [PubMed]
17. Kavitha CT, Chellamuthu C. Medical image fusion based on hybrid intelligence. Applied Soft Computing 2014;20:83-94. [Crossref]
18. Xu X, Shan D, Wang G, et al. Multimodal medical image fusion using PCNN optimized by the QPSO algorithm. Applied Soft Computing 2016;46:588-95. [Crossref]
19. Liu Y, Chen X, Peng H, et al. Multi-focus image fusion with a deep convolutional neural network. Information Fusion 2017;36:191-207. [Crossref]
20. Bhatnagar G, Wu QMJ, Liu Z. Human visual system inspired multi-modal medical image fusion framework. Expert Syst Appl 2013;40:1708-20. [Crossref]
21. Das S, Kundu MK. A neuro-fuzzy approach for medical image fusion. IEEE Trans Biomed Eng 2013;60:3347-53. [Crossref] [PubMed]
22. Daniel E, Anitha J, Gnanaraj J. Optimum laplacian wavelet mask based medical image using hybrid cuckoo search–grey wolf optimization algorithm. Knowledge-Based Systems 2017;131:58-69. [Crossref]
23. Daniel E, Anitha J, Kamaleshwaran KK, et al. Optimum spectrum mask based medical image fusion using Gray Wolf Optimization. Biomed Signal Process Control 2017;34:36-43. [Crossref]
24. Daniel E, Anitha J. Optimum wavelet based masking for the contrast enhancement of medical images using enhanced cuckoo search algorithm. Comput Biol Med 2016;71:149-55. [Crossref] [PubMed]
25. Li S, Kang X, Fang L, et al. Pixel-level image fusion: A survey of the state of the art. Information Fusion 2017;33:100-12. [Crossref]
26. Iwatsuki M, Harada K, Baba H, et al. Higher rate of colon polyp detection aided by an artificial intelligent software. Transl Gastroenterol Hepatol 2018;3:106. [Crossref] [PubMed]
27. Wu Y, Jiang JH, Chen L, et al. Use of radiomic features and support vector machine to distinguish Parkinson's disease cases from normal controls. Ann Transl Med 2019;7:773. [Crossref] [PubMed]
28. Oliveira FP, Tavares JM. Medical image registration: a review. Comput Methods Biomech Biomed Engin 2014;17:73-93. [Crossref] [PubMed]
29. Zhang X, He Y, Jia K, et al. Does selected immunological panel possess the value of predicting the prognosis of early-stage resectable non-small cell lung cancer? Transl Lung Cancer Res 2019;8:559-74. [Crossref] [PubMed]
30. Oliveira FP, Pataky TC, Tavares JM. Registration of pedobarographic image data in the frequency domain. Comput Methods Biomech Biomed Engin 2010;13:731-40. [Crossref] [PubMed]
31. Adelmann HG. Butterworth equations for homomorphic filtering of images. Comput Biol Med 1998;28:169-81. [Crossref] [PubMed]
32. Eberhart R, Kennedy J. A new optimizer using particle swarm theory. MHS'95. Proceedings of the Sixth International Symposium on Micro Machine and Human Science. IEEE, 1995.
33. Kuo RJ, Hong SY, Huang Y. Integration of particle swarm optimization-based fuzzy neural network and artificial neural network for supplier selection. Applied Mathematical Modelling 2010;34:3976-90. [Crossref]
34. Lai GH, Chen CM, Jeng BC, et al. Ant-based IP traceback. Expert Syst Appl 2008;34:3071-80. [Crossref]
35. Liu Y, Liu S, Wang Z. A general framework for image fusion based on multi-scale transform and sparse representation. Information Fusion 2015;24:147-64. [Crossref]
36. Zhuang Y, Gao K, Miu X, et al. Infrared and visual image registration based on mutual information with a combined particle swarm optimization–Powell search algorithm. Optik 2016;127:188-91. [Crossref]
37. Li J, Peng Z. Multi-source image fusion algorithm based on cellular neural networks with genetic algorithm. Optik 2015;126:5230-6. [Crossref]
38. Cao L, Jin L, Tao H, et al. Multi-focus image fusion based on spatial frequency in discrete cosine transform domain. IEEE Signal Processing Letters 2015;22:220-4. [Crossref]
39. Vijayarajan R, Muttan S. Discrete wavelet transform based principal component averaging fusion for medical images. Int J Electron Commun 2015;69:896-902. [Crossref]
40. Sharma JB, Sharma KK, Sahula V. Hybrid image fusion scheme using self-fractional Fourier functions and multivariate empirical mode decomposition. Signal Processing 2014;100:146-59. [Crossref]
41. He C, Liu Q, Li H, et al. Multimodal medical image fusion based on IHS and PCA. Procedia Engineering 2010;7:280-5. [Crossref]

(English Language Editor: J. Chapnick)