
Development and application of a dynamic prediction model for esophageal cancer
Introduction
Esophageal cancer (EC) is a malignant tumor with an extremely poor prognosis, with a 5-year overall survival (OS) rate of approximately 20% (1). Different pathological types of EC differ greatly in terms of their male to female ratio, time trends, geographic patterns, and primary risk factors across countries (2-4). These diverse characteristics can interact with survival outcomes, making it difficult to obtain estimations of individual prognosis. Therefore, there is an urgent need for accurate survival prediction tools that take into account the heterogeneity of patients to help clinicians predict individual survival and propose treatment recommendations. A recent systematic review indicated that there were at least 15 prediction models for EC patients between January 1st, 2000 and February 6th, 2017 (5). However, most previous prediction models were developed using the Cox proportional hazards model, which fundamentally assumes that the hazard ratio of covariates does not change with time (6). However, several studies have discovered that some prognostic variables may exhibit time-varying effects on the outcome, leading to changes in mortality risk over time (7-12). Therefore, these predicted results could be misleading if covariates exhibit time-varying effects.
In addition, there is a practical problem that the currently available prediction models cannot solve in the study of EC. For example, a patient may pay more attention to the survival probability or mortality of “w” years after a cancer diagnosis, which is often asked by questions such as: “How long will I live?” or “What is the probability of being alive ‘w’ years from now?” Furthermore, these questions are not only asked at diagnosis, but also at any time during the follow-up (FU) visits. However, most existing prediction models ignore this issue because they were designed only based on the patient’s baseline status at diagnosis or at a specific time during treatment, and ultimately obtain a corresponding 3- or 5-year survival rate. However, they are unable to calculate survival probabilities at different time points and therefore cannot reflect the change in patient survival probability during the follow-up period. Therefore, van Houwelingen et al. proposed a new dynamic prediction model based on the proportional baselines landmark supermodel (PBLS), which takes time-varying effects into account and is able to update survival probabilities over time (13,14). The predicted 5-year OS probability is known as a 5-year dynamic overall survival (DOS). Our previous research has compared the effect of using the PBLS versus the Cox proportional hazards model when constructing a cervical cancer prediction model in the context of time-varying effects. We found that with the time-varying effects, the PBLS model was recommended to predict a patient’s w year dynamic survival rate (15). To the best of our knowledge, no previous dynamic prediction model based on the PBLS has been developed for patients with EC.
The aim of this research was to explore covariates with time-varying effects in EC and to develop a universally applicable and accurate prediction model that can dynamically predict survival probabilities for patients with EC during the entire follow-up period. Therefore, a prediction model with time-varying effects was developed and internally validated using the Surveillance, Epidemiology, and End Results (SEER) database. Moreover, an independent Chinese EC patient cohort was used for external validation of the model. The resulting model can predict an individual patient’s 5-year survival probability at different prediction time points up to 5 years after EC diagnosis. Specific patient examples were also used to illustrate how predicted survival probabilities vary at different time points during follow-up and how the model can assist clinicians in their medical practice. Compared with previous studies, the innovation of our model was that the variables with time-varying effects were taken into account, which enabled the model to dynamically predict the survival probabilities of patients at different time points during the follow-up period. We present the following article in accordance with the TRIPOD reporting checklist (available at https://dx.doi.org/10.21037/atm-21-4964).
Methods
Data source
The SEER database is a population-based cancer database that covers approximately 28% of the U.S. population. Patient information, including demographics, clinical characteristics, pathological features, treatment, and survival data were downloaded from the SEER 18 Regs Custom Data (with additional treatment) released in November 2018 Sub [1975–2016] using SEER*Stat version 8.3.6. The information of 19,362 cases of patients with microscopically-confirmed EC was extracted between January 2007 and December 2011. Only histologic codes for squamous cell cancers (ICD-O-3 histology codes: 8000-8046, 8051-8131, 8148-8157, 8230-8249, 8508, 8510-8513, 8560-8570, 8575, 8950, 8980-8981) and adenocarcinoma (codes: 8050, 8140-8147, 8160-8162, 8170-8175, 8180-8221, 8250-8507, 8514-8551, 8514-8551, 8576, 8940-8941, 8140-8573) were included in the research.
Cohort selection
Baseline patient- and tumor-specific factors included in the model were as follows: age at diagnosis, marital status, race, sex, histological type, primary tumor site, grade, T stage, N stage, M stage, surgery primary site, radiation, chemotherapy, survival months, and vital status. The period was restricted between 2007 and 2011, during which patient pathological staging was characterized according to the American Joint Committee on Cancer (AJCC) Tumor Node Metastasis (TNM) sixth edition staging criteria.
The exclusion criteria were as follows: (I) patients who were not diagnostically confirmed by positive histology (N=904); (II) those whose tumor was not the first malignant primary indicator (N=4,992); (III) patients whose reporting source was an autopsy, hospice, death certificate, or nursing home (N=204); (IV) those with an unknown marital status (N=648); (V) patients of unknown or American Indian/Alaska Native race (N=87); (VI) those with a primary tumor site code C15.1 or C15.9 (N=1,484); (VII) patients whose histologic type was not adenocarcinoma or squamous cell carcinoma (N=26); (VIII) those lacking a histological grade (N=1,832); (IX) patients with an unknown (N=1,869) or T0 T stage (N=4); (X) those without specific N and M stages (N=384); (XI) patients with a surgery primary site code 10–27 (local tumor excision, N=23); (XII) those with a surgery primary site code 90 (NOS, N=23) or 99 (unknown, N=9); (XIII) patients with a radiation code radioisotopes (N=1); and (XIV) those with unknown or <3 survival months (N=1,302). Finally, 5,423 patients were eligible for inclusion in this study. These patients were randomly divided into a training cohort (N=4,541) and an internal validation cohort (N=882) at a ratio of 5:1. The screening process is presented in detail in Figure 1.
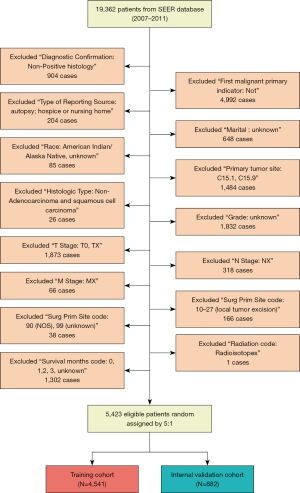
The eligible data were defined, integrated, and grouped. First, data were divided by age into five groups: age <50, 50–59, 60–69, 70–79, and >80 years. Patients who were separated, divorced, single patients (never married), or widowed at diagnosis were integrated into the unmarried group, and married patients (including common-law marriages) were designated as the married group. Tumor sites were divided into four groups: upper third of the esophagus (C15.0, C15.3), middle third of the esophagus (C15.4), lower third of the esophagus (C15.2, C15.5), and overlapping lesion of the esophagus (C15.8). Patients were grouped into radiotherapy and no radiotherapy/unknown groups based on their radiotherapy treatment. Surgery primary site reflected whether the patient has undergone surgery and the surgical site. Thus, patients in this study were divided into surgery (codes: 30–80) and no surgery (codes: 0) groups.
A retrospective Chinese patient cohort consisting of 99 EC patients from the Zhujiang Hospital of the Southern Medical University (Guangzhou, Guangdong Province, China) between January 2004 and September 2010 was used to externally validate this dynamic prediction model. The inclusion and exclusion criteria for all cases were the identical to the screening criteria for the SEER database. All procedures performed in this study involving human participants were in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by the Medical Ethics Committee of Zhujiang Hospital, Southern Medical University, Guangzhou, China (ethics committee approval number: 2020-KY-001-01). Individual consent for this retrospective analysis was waived. Using SEER data does not require additional informed consent as patient privacy information is protected by the SEER cancer registries.
Statistical analysis
All-cause mortality (death from any cause) served as the primary endpoint in this study. Survival time was measured in years from the date of diagnosis until (I) the date of death, (II) the date last known to be alive, or (III) December 31, 2016.
The categorical data were indicated as frequencies (percentages). The Kaplan-Meier curves of OS were compared using the log-rank test. The univariable and multivariable Cox proportional hazard (PH) models were used to estimate hazard ratios (HRs) and 95% confidence intervals (CIs). The PHs assumption was checked using the Grambsch-Therneau test. A PBLS (for more details, see Supplemental method I) was established to obtain the 5-year DOS. Firstly, the prediction window was fixed at w=5, where w was the patient’s response to the question “How long will I live?” at any prediction time point (). Next, a set of prediction landmark time points was selected at every third month between 0 and 5 years after the diagnosis of EC (see the blue circles and the yellow parts in Figure S1). A Cox PH model for 5-year OS at a specific s was then estimated on the subset of patients, who were still alive at s and administrative censored at s + w (see the red circles and the blue parts in Figure S1). A super prediction data set (for construction, see Supplemental method II) was stacked with all-created small subsets (the number of patients in each landmark subset is shown in Figure S2). The following model was constructed for our study, where and .
A backward selection procedure was then used to select covariates with time-varying effects in two steps. Initially, all of the interactions (Z × s2) between quadratic s2 and the covariates were tested, and non-significant terms were then removed. In the second step, interactions (Z × s2) for linear s and prognostic factors were tested, and only significant effects were retained. The w-year dynamic HR at different time points could then be calculated using the following equations:
The performance of the model was evaluated in terms of both discrimination and calibration. The model’s ability to correctly discriminate between patients was evaluated using the area under the curve (AUC). Calibration was evaluated using the heuristic shrinkage factor. All analyses were performed using R software (version 3.6.1) (https://www.r-project.org/), and the significance level was set at 0.05.
Results
Patient characteristics
A total of 5,423 EC patients from the SEER database were included in the analyses. 4,541 randomly-assigned patients were used as the training cohort for the development of the prediction model, and 882 patients were used as the internal validation cohort for the model. The median follow-up time for the training cohort was 16.00 (95% CI: 15.31–16.69) months (range, 4–119 months), while the 3- and 5-year survival rates of the training cohort were 27.99% (95% CI: 26.71–29.32%) and 20.28% (95% CI: 19.14–21.49%), respectively. The median follow-up time for the interval validation cohort was 18.00 (95% CI: 16.19–19.81) months (range, 4–119 months), while the 3- and 5-year survival rates of the interval validation cohort were 28.53% (95% CI: 25.70–31.68%) and 21.01% (95% CI: 18.46–23.90%), respectively. A total of 99 patients from a Chinese patient cohort were investigated as the external validation cohort. Their median follow-up time was 13.00 (95% CI: 10.94–15.07) months (range, 2–98 months), and the 3- and 5-year survival rates of the entire cohort were 15.15% (95% CI: 9.51–24.15%) and 9.26% (95% CI: 4.78–17.96%), respectively. The OS curves of the three cohorts are shown in Figure 2. The baseline demographics and tumor characteristics of the included patients are presented in Table 1. The Kaplan-Meier survival curves (Figure S3) for age at diagnosis, sex, T stage, chemotherapy, and radiotherapy had intersecting evidence. Moreover, the Cox PH model (Table S1) could not satisfy the PH assumption that the HR is constant over time. To obtain the 5-year DOS, we used the PBLS to analyze our study.
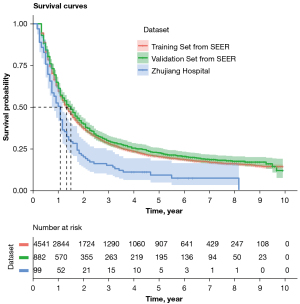
Table 1
| Characteristics | Training cohort (N=4,541) | Internal validation (N=882) | External validation (N=99) | |||||
|---|---|---|---|---|---|---|---|---|
| n | % | n | % | n | % | |||
| Age | ||||||||
| <50 years | 416 | 9.16 | 79 | 8.96 | 1 | 1.01 | ||
| 50–59 years | 1,105 | 24.33 | 206 | 23.36 | 42 | 42.42 | ||
| 60–69 years | 1,572 | 34.62 | 311 | 35.26 | 33 | 33.33 | ||
| 70–79 years | 1,008 | 22.20 | 190 | 21.54 | 13 | 13.13 | ||
| 80+ years | 440 | 9.69 | 96 | 10.88 | 2 | 2.02 | ||
| Sex | ||||||||
| Male | 823 | 18.12 | 136 | 15.42 | 80 | 80.81 | ||
| Female | 3,718 | 81.88 | 746 | 84.58 | 19 | 19.19 | ||
| Marriage status | ||||||||
| Married | 2,807 | 61.81 | 561 | 63.61 | 99 | 100.00 | ||
| Unmarried | 1,734 | 38.19 | 321 | 36.39 | 0 | 0.00 | ||
| Race | ||||||||
| Asian or Pacific islander | 205 | 4.51 | 35 | 3.97 | 99 | 100.00 | ||
| Black | 423 | 9.32 | 74 | 8.39 | 0 | 0.00 | ||
| White | 3,913 | 86.17 | 773 | 87.64 | 0 | 0.00 | ||
| Histological types | ||||||||
| Squamous cell carcinoma | 1,409 | 31.03 | 260 | 29.48 | 91 | 91.92 | ||
| Adenocarcinoma | 3,132 | 68.97 | 622 | 70.52 | 8 | 8.08 | ||
| Primary tumor site | ||||||||
| Upper third of esophagus | 289 | 6.36 | 44 | 4.99 | 10 | 10.10 | ||
| Middle third of esophagus | 703 | 15.48 | 126 | 14.29 | 40 | 40.40 | ||
| Lower third of esophagus | 3,375 | 74.32 | 679 | 76.98 | 20 | 20.20 | ||
| Overlapping lesion | 174 | 3.83 | 33 | 3.74 | 29 | 29.29 | ||
| Grade | ||||||||
| Grade I | 261 | 5.75 | 45 | 5.10 | 6 | 6.06 | ||
| Grade II | 1,926 | 42.41 | 380 | 43.08 | 62 | 62.63 | ||
| Grade III/grade IV | 2,354 | 51.84 | 457 | 51.81 | 31 | 31.31 | ||
| T stage | ||||||||
| T1 | 1,366 | 30.08 | 240 | 27.21 | 3 | 3.03 | ||
| T2 | 607 | 13.37 | 127 | 14.40 | 11 | 11.11 | ||
| T3 | 1,970 | 43.38 | 412 | 46.71 | 63 | 63.64 | ||
| T4 | 598 | 13.17 | 103 | 11.68 | 22 | 22.22 | ||
| N stage | ||||||||
| N0 | 1,953 | 43.01 | 392 | 44.44 | 39 | 39.39 | ||
| N1 | 2,588 | 56.99 | 490 | 55.56 | 60 | 60.61 | ||
| M stage | ||||||||
| M0 | 3,302 | 72.72 | 658 | 74.60 | 79 | 79.80 | ||
| M1 | 1,239 | 27.28 | 224 | 25.40 | 20 | 20.20 | ||
| Surgery | ||||||||
| Yes | 1,795 | 39.53 | 352 | 39.91 | 68 | 68.69 | ||
| No/unknown | 2,746 | 60.47 | 530 | 60.09 | 31 | 31.31 | ||
| Chemotherapy | ||||||||
| Yes | 3,520 | 77.52 | 670 | 75.96 | 69 | 69.70 | ||
| No/unknown | 1,021 | 22.48 | 212 | 24.04 | 30 | 30.30 | ||
| Radiation | ||||||||
| Yes | 3,185 | 70.14 | 597 | 67.69 | 43 | 43.43 | ||
| No/unknown | 1,356 | 29.86 | 285 | 32.31 | 56 | 56.57 | ||
Variables with time-constant and time-varying effects
Regression coefficients and HRs with 95% CI for the variables included in the model are represented in Table 2 and Figure 3. Variables with time-constant and time-varying effects on the 5-year DOS were also determined. Patient baseline demographics and tumor characteristics, including marital status, race, grade, N stage, M stage, and radiotherapy, had a time-constant effect (Table 2, Figure 3). The HR for these variables was constant regardless of time point during the follow-up period (Figure 3B,3C,3G,3I,3J,3M). For instance, the HR for unmarried patients compared to married patients was 1.156 (95% CI: 1.061–1.260) at the time of diagnosis with EC (0 years). During the following 5 years after diagnosis, the HR value remained at 1.156, demonstrating a significant time-constant effect (Figure 3B).
Table 2
| Covariates | Regression coefficient | Hazard ratio | (95% CI) | P value |
|---|---|---|---|---|
| Covariates with time-constant effects | ||||
| Marriage status (ref: married) | ||||
| Unmarried | 0.145 | 1.156 | 1.061–1.260 | 0.001 |
| Race (ref: White) | ||||
| Black | 0.172 | 1.187 | 1.024–1.377 | 0.023 |
| Asian or Pacific Islander | −0.195 | 0.823 | 0.675–1.004 | 0.055 |
| Grade (ref: grade I) | ||||
| Grade II | 0.187 | 1.206 | 1.005–1.447 | 0.044 |
| Grade III/grade IV | 0.353 | 1.424 | 1.187–1.708 | <0.001 |
| N stage (ref: N0) | ||||
| N1 | 0.238 | 1.269 | 1.162–1.386 | <0.001 |
| M stage (ref: M0) | ||||
| M1 | 0.391 | 1.479 | 1.332–1.642 | <0.001 |
| Radiation (ref: yes) | ||||
| No/unknown | −0.019 | 0.981 | 0.880–1.094 | 0.735 |
| Covariates with time-varying effects | ||||
| Age at diagnosis (ref: per 10 years) | ||||
| Constant | ||||
| Age | 0.075 | 1.078 | 1.042–1.116 | <0.001 |
| Time-varying effect | ||||
| Age (s) | −0.111 | 0.895 | 0.715–1.121 | 0.334 |
| Age (s2) | 0.450 | 1.568 | 1.161–2.119 | 0.003 |
| Sex (ref: female) | ||||
| Constant | ||||
| Male | 0.175 | 1.192 | 1.066–1.332 | 0.002 |
| Time-varying effect | ||||
| Male (s) | 0.664 | 1.943 | 1.287–2.935 | 0.002 |
| Histological types (ref: adenocarcinoma) | ||||
| Constant | ||||
| Squamous cell carcinoma | −0.020 | 0.980 | 0.879–1.092 | 0.715 |
| Time-varying effect | ||||
| Squamous cell carcinoma (s) | −0.815 | 0.443 | 0.257–0.764 | 0.003 |
| Squamous cell carcinoma (s2) | 0.892 | 2.441 | 1.331–4.476 | 0.004 |
| Primary tumor site (ref: lower) | ||||
| Constant | ||||
| Upper | −0.076 | 0.926 | 0.779–1.101 | 0.387 |
| Middle | 0.018 | 1.018 | 0.894–1.159 | 0.788 |
| Overlapping | 0.296 | 1.344 | 1.110–1.628 | 0.002 |
| Time-varying effect | ||||
| Upper (s) | 0.238 | 1.269 | 0.660–2.439 | 0.475 |
| Middle (s) | 0.563 | 1.756 | 1.170–2.636 | 0.007 |
| Overlapping (s) | −0.087 | 0.917 | 0.355–2.366 | 0.857 |
| Chemotherapy (ref: yes) | ||||
| Constant | ||||
| No/unknown | 0.216 | 1.241 | 1.107–1.391 | <0.001 |
| Time-varying effect | ||||
| No/unknown (s) | −1.379 | 0.252 | 0.138–0.460 | <0.001 |
| No/unknown (s2) | 1.135 | 3.111 | 1.589–6.093 | 0.001 |
| Surgery (ref: yes) | ||||
| Constant | ||||
| No | 0.863 | 2.370 | 2.152–2.611 | <0.001 |
| Time-varying effect | ||||
| No (s) | −0.738 | 0.478 | 0.346–0.661 | <0.001 |
| T stage (ref: T1) | ||||
| Constant | ||||
| T2 | −0.057 | 0.945 | 0.829–1.076 | 0.393 |
| T3 | 0.199 | 1.220 | 1.103–1.349 | <0.001 |
| T4 | 0.300 | 1.350 | 1.184–1.539 | <0.001 |
| Time-varying effect | ||||
| T2 (s) | 0.598 | 1.818 | 1.191–2.776 | 0.006 |
| T3 (s) | 0.282 | 1.326 | 0.917–1.919 | 0.134 |
| T4 (s) | 0.417 | 1.517 | 0.888–2.592 | 0.127 |
| Prediction time (ref: years since start of diagnosis) | ||||
| s | 2.648 | 14.128 | 2.861–69.756 | 0.001 |
| s2 | −4.016 | 0.018 | 0.004–0.074 | <0.001 |
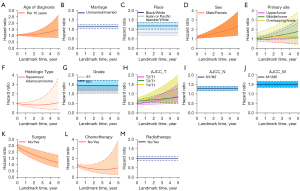
On the contrary, age at diagnosis, sex, primary tumor site, histologic type, stage AJCC T, surgery, and chemotherapy demonstrated significant time-varying effects on the 5-year DOS. These HRs were constantly changing with each successive s (Figure 3A,3D,3E,3F,3H,3K,3L). For example, the HR value for a patient without chemotherapy immediately after primary treatment compared to a patient with chemotherapy (Yes) was 1.241, which was calculated using the following formula (Table 2): . This value decreased to 0.986 after 1 year of follow-up, 0.816 after 3 years of follow-up, and 0.972 after 5 years of follow-up (Figure 3L). Age, sex, primary tumor site, histologic type, chemotherapy, and AJCC T stage also demonstrated a significant time-varying effect.
Internal model validation
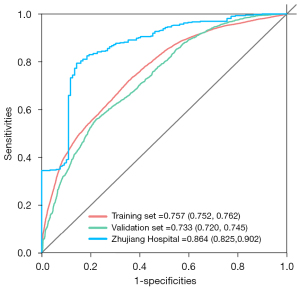
The heuristic shrinkage factor was 0.995, which indicated good model calibration. The model discriminatory accuracy was verified using the SEER validation cohort using the AUC, resulting in values of 0.763 (95% CI: 0.745–0.78), 0.746 (95% CI: 0.732–0.760), and 0.733 (95% CI: 0.720–0.745) at 1, 2, and 3 years, respectively, and self-verified by training cohort, resulting in values of 0.784 (95% CI: 0.776–0.791), 0.767 (95% CI: 0.761–0.773), and 0.757 (95% CI: 0.752–0.762) at 1, 2, and 3 years, respectively (Figure 4), which both reflected satisfactory accuracy.
External model validation
A retrospective Chinese patient cohort consisting of 99 EC patients from Zhujiang Hospital of the Southern Medical University (Guangzhou, Guangdong Province, China) between January 2004 and September 2010 was used for external model validation. Model discriminatory accuracy was verified using the AUC, resulting in values of 0.865 (95% CI: 0.811–0.919), 0.871 (95% CI: 0.827–0.914), and 0.864 (95% CI: 0.825–0.902) at 1, 2, and 3 years respectively (Figure 4).
Model application
The most important function of the dynamic prediction model is to intuitively portray the change in patient survival probability, in order to assist clinicians in performing their medical practice. Our study selected 14 patients as examples for model application to respectively demonstrate the impact of different variables’ time-varying effect on survival and to map the patient’s 5-year DOS curves (Figure 5).
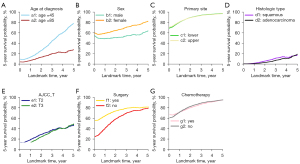
For instance, clinicians often face the problem of receiving adjuvant chemotherapy after an esophagectomy for an early EC patient. In this case, clinicians can use the dynamic survival prediction model to map the survival curves under different conditions for clinical decision-making. Figure 5G displays the 5-year probabilities of survival for a 55-year-old married Caucasian female patient with esophageal adenocarcinoma in the lower third of the esophagus, diagnosed with T1N1M0 stage, and treated with an esophagectomy. The g1 line shows the 5-year survival probability for this patient receiving adjuvant chemotherapy after esophagectomy. Conversely, the g2 line shows the survival probability for this patient without receiving adjuvant chemotherapy after esophagectomy. It is evident that postoperative adjuvant chemotherapy increases the survival probability for this patient in the early follow-up phase (time point = 0–1 years), but subsequently resulted in a lower survival probability during the follow-up period. This example shows that this model can assist doctors in developing individualized treatment strategies for patients.
The latest National Comprehensive Cancer Network (NCCN) clinical practice guidelines for EC recommend that patients with early EC undergo radical surgery. However, many patients will refuse surgery for various reasons. In this case, patients can be educated using dynamic survival curves resulting from this prediction model. For example, Figure 5F demonstrates a 55-year-old married Asian male patient diagnosed with squamous cell carcinoma in the middle third of the esophagus, with a stage of T1N0M0. The f1 line shows the 5-year survival probability for this patient receiving radical surgery for EC. Conversely, the f2 line shows this patient’s survival probability without receiving radical surgery. The 5-year dynamic survival curves suggest that in the early follow-up phase for this patient, the 5-year survival rate after undergoing radical surgery is significantly higher than that after refusing surgery. Although the gap will be shortened over time, this still underscores the importance of radical surgery for patients with early EC. There are also several additional examples shown in Figure 5, which are not elaborated in the article, and detailed patient information is attached to Table S2.
In clinical practice, this model can be used for EC patients to predict their 5-year survival probabilities at different time points during the follow-up period. In addition, this model can map patient-specific dynamic survival curves to assist clinicians in their practice.
Discussion
To the best of our knowledge, there are few prediction models for EC that can dynamically predict 5-year OS at a specific time point during follow-up after diagnosis. The main highlight of this model is that it takes into account prognostic variables with time-varying effects, including age, sex, primary tumor site, histologic type, chemotherapy, surgery, and AJCC T stage. The discovery and addition of time-varying effects in the model make its predicted results more optimal because the model can adjust the HR of prognostic variables, thereby adjusting the patient’s survival probability at different time points. Most importantly, the prominent advantage of this model is that it can predict the 5-year survival probability of patients at different time points, making the prediction more accurate and more practical.
Several EC prediction models currently exist. These models have different manifestation forms, prognostic covariates, use conditions, and predictive purposes. For example, Eil et al. created a web-based prediction tool to determine the OS of patients treated with esophagectomy or neoadjuvant chemoradiotherapy followed by esophagectomy (16). The covariates included in the model were sex, T and N classification, histology, the total number of lymph nodes examined, and treatment. Cao et al. used a population-based SEER database for constructing a nomogram to predict patient survival esophagectomy (17), which incorporated covariates such as age at diagnosis, recorded race, histological type, tumor site and size, grade, T category, N category, and retrieved lymph nodes. Custodio et al. developed a survival prediction model for Caucasian patients with advanced esophagogastric adenocarcinoma receiving first-line chemotherapy (18). Tang et al. developed a model predicting cancer-specific survival for patients initially diagnosed with metastatic EC (mEC) (19). The novelty of this study was that it filled the gap in predicting mEC.
Numerous studies have demonstrated that some prognostic variables may exhibit time-varying effects that result in a change in the HR over time during long-term follow-up. These variables include age at diagnosis (20,21), tumor size (8,21,22), lymph nodal status (8,21), tumor stage (23), histological grade (8,9,24), hormone receptors status (9,24), tumor biomarker level (10), drug exposure, and chemotherapy (21,25). In addition, Fontein et al. demonstrated that high-risk N-stage (N2/3), Human Epidermal Growth Factor Receptor 2-positive (HER2 -positive), and locoregional recurrence are all characteristics that have time-varying effects in postmenopausal, endocrine-sensitive breast cancer patients, and further designed a dynamic prediction model that can update predictions at different time points (26). Rueten-Budde et al. determined that surgical margin and tumor histology exhibit significant time-varying effects on OS, and modeled a dynamic prediction for patients with high-grade extremity soft tissue sarcoma (27). However, the EC prediction models above did not take into account that some predictive variables may have time-varying effects. Moreover, these models are not able to update predictions at different time points during the follow-up period. To date, there is no existing EC prediction model that involves variables with time-varying effects and can dynamically predict the survival probability of patients at different time points.
The present study explored the effect of predictive variables over time in EC and found significant time-varying effects of age, sex, primary tumor site, histologic type, chemotherapy, surgery, and T stage on OS. We then developed a prediction model based on the PBLS, which takes into account variables with time-varying effects. Many studies have shown that the prognostic effect of age on survival changes during long-term follow-up, which is similar to our results on the time-varying effect of age (20,21). Chemotherapy has also been shown to have time-varying effects in several studies, which is consistent with our findings (21,25). No previous research has discovered the time-varying effects of the remaining five prognostic factors, which therefore deserve further investigation. The accumulation and interaction of these time-varying effects result in a change in the risk of death for EC patients and lead to a dynamic prediction of survival probabilities. Compared with other ‘static’ prediction models, the advantages of this model were to take into account variables with time-varying effects for the first time in EC, so that the model has the ability to dynamically predict and update survival probabilities at different time points.
Owing to its ability to predict survival probabilities dynamically, this model can play an important role in practical applications. As mentioned above, when faced with the tricky problem of postoperative adjuvant chemotherapy benefit for a T1N1M0 EC patient after surgery, clinicians can use the dynamic prediction model to calculate the 5-year DOS for both chemotherapy and non-chemotherapy at different time points during the follow-up period, and choose the treatment according to its predictive results. In conclusion, this dynamic prediction model can make predictions more accurate by updating the survival probabilities over time, and can assist clinicians in patient counseling, individualized therapy decision-making, and treatment risk evaluation.
Several limitations exist in this dynamic prediction model. The retrospective nature of the SEER database data, as well as a large number of missing patient clinical pathology registration information are the main limitations of this study. Also, since the data used to construct the model is retrospective, a lot of registered information (which used an early classification version, such as the AJCC-TNM 6th edition staging criteria) was included in the present model, with subtle time differences in clinical applications. Moreover, some important variables that may alter patient prognosis during the follow-up period, such as locoregional and distant recurrences, were not included in the present study, as this information is not registered in the SEER database. For the same reason, the lack of treatment-related variables, such as induction chemoradiotherapy, the quality of esophagectomy, surgical margins, degree of response to therapy, and comorbidity information, also represent disadvantages of the model. Finally, this prediction model could benefit from presentation in an easy-to-use medium, such as a nomogram, web-based calculator, or mobile application.
Conclusions
This study explored and discovered variables that exhibit time-varying effects in EC, and then developed a prediction model that can predict survival probabilities at different time points in the follow-up period. Our dynamic prediction model can continuously revise the patient residual death risk and track changes in patient survival, thereby assisting clinicians in selecting individualized therapy. Additionally, this study underscores the importance of using prediction models for clinical guidance, not only at the time of diagnosis but also during the follow-up period.
Acknowledgments
Funding: This work is supported by a grant from the National Natural Science Foundation of China (No. 81974434), and a grant from the Natural Science Foundation of Guangdong Province (No. 2020A0505100038), grant from the Science and Technology Program of Guangzhou City (No. 201907010037), grant from the Affiliated Cancer Hospital & Institute of Guangzhou Medical University (No. 2020-YZ-01), and grant from Clinical Key Specialty Construction Project of Guangzhou Medical University (No. YYPT202017).
Footnote
Reporting Checklist: The authors have completed the TRIPOD reporting checklist. Available at https://dx.doi.org/10.21037/atm-21-4964
Data Sharing Statement: Available at https://dx.doi.org/10.21037/atm-21-4964
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://dx.doi.org/10.21037/atm-21-4964). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. All procedures performed in this study involving human participants were in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by the Medical Ethics Committee of Zhujiang Hospital, Southern Medical University, Guangzhou, China (ethics committee approval number: 2020-KY-001-01). Individual consent for this retrospective analysis was waived. Using the SEER data did not require additional informed consent as patient privacy information is protected by the SEER cancer registries.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Jemal A, Ward EM, Johnson CJ, et al. Annual Report to the Nation on the Status of Cancer, 1975-2014, Featuring Survival. J Natl Cancer Inst 2017;109:djx030 [Crossref] [PubMed]
- Coleman HG, Xie SH, Lagergren J. The Epidemiology of Esophageal Adenocarcinoma. Gastroenterology 2018;154:390-405. [Crossref] [PubMed]
- Abnet CC, Arnold M, Wei WQ. Epidemiology of Esophageal Squamous Cell Carcinoma. Gastroenterology 2018;154:360-73. [Crossref] [PubMed]
- Cook MB, Chow WH, Devesa SS. Oesophageal cancer incidence in the United States by race, sex, and histologic type, 1977-2005. Br J Cancer 2009;101:855-9. [Crossref] [PubMed]
- van den Boorn HG, Engelhardt EG, van Kleef J, et al. Prediction models for patients with esophageal or gastric cancer: A systematic review and meta-analysis. PLoS One 2018;13:e0192310 [Crossref] [PubMed]
- Cox DR. Regression models and life-tables. J Royal Stat Soc (B) 1972;34:187-220. [Crossref]
- Fisher LD, Lin DY. Time-dependent covariates in the Cox proportional-hazards regression model. Annu Rev Public Health 1999;20:145-57. [Crossref] [PubMed]
- Warwick J, Tabàr L, Vitak B, et al. Time-dependent effects on survival in breast carcinoma: results of 20 years of follow-up from the Swedish Two-County Study. Cancer 2004;100:1331-6. [Crossref] [PubMed]
- Baulies S, Belin L, Mallon P, et al. Time-varying effect and long-term survival analysis in breast cancer patients treated with neoadjuvant chemotherapy. Br J Cancer 2015;113:30-6. [Crossref] [PubMed]
- Chang C, Chiang AJ, Wang HC, et al. Evaluation of the Time-Varying Effect of Prognostic Factors on Survival in Ovarian Cancer. Ann Surg Oncol 2015;22:3976-80. [Crossref] [PubMed]
- Rakovitch E, Sutradhar R, Hallett M, et al. The time-varying effect of radiotherapy after breast-conserving surgery for DCIS. Breast Cancer Res Treat 2019;178:221-30. [Crossref] [PubMed]
- Rogoz B, Houzé de l'Aulnoit A, Duhamel A, et al. Thirty-Year Trends of Survival and Time-Varying Effects of Prognostic Factors in Patients With Metastatic Breast Cancer-A Single Institution Experience. Clin Breast Cancer 2018;18:246-53. [Crossref] [PubMed]
- van Houwelingen HC. Dynamic prediction by landmarking in event history analysis. Scandinavian Journal of Statistics 2007;34:70-85. [Crossref]
- Houwelingen HV, Putter H. Dynamic Prediction in Clinical Survival Analysis. Lyon: CRC Press; 2012.
- Li L, Yang Z, Hou Y, et al. Moving beyond the Cox proportional hazards model in survival data analysis: a cervical cancer study. BMJ Open 2020;10:e033965 [Crossref] [PubMed]
- Eil R, Diggs BS, Wang SJ, et al. Nomogram for predicting the benefit of neoadjuvant chemoradiotherapy for patients with esophageal cancer: a SEER-Medicare analysis. Cancer 2014;120:492-8. [Crossref] [PubMed]
- Cao J, Yuan P, Wang L, et al. Clinical Nomogram for Predicting Survival of Esophageal Cancer Patients after Esophagectomy. Sci Rep 2016;6:26684. [Crossref] [PubMed]
- Custodio A, Carmona-Bayonas A, Jiménez-Fonseca P, et al. Nomogram-based prediction of survival in patients with advanced oesophagogastric adenocarcinoma receiving first-line chemotherapy: a multicenter prospective study in the era of trastuzumab. Br J Cancer 2017;116:1526-35. [Crossref] [PubMed]
- Tang X, Zhou X, Li Y, et al. A Novel Nomogram and Risk Classification System Predicting the Cancer-Specific Survival of Patients with Initially Diagnosed Metastatic Esophageal Cancer: A SEER-Based Study. Ann Surg Oncol 2019;26:321-8. [Crossref] [PubMed]
- Jørgensen TL, Teiblum S, Paludan M, et al. Significance of age and comorbidity on treatment modality, treatment adherence, and prognosis in elderly ovarian cancer patients. Gynecol Oncol 2012;127:367-74. [Crossref] [PubMed]
- Tanis E, van de Velde CJ, Bartelink H, et al. Locoregional recurrence after breast-conserving therapy remains an independent prognostic factor even after an event free interval of 10 years in early stage breast cancer. Eur J Cancer 2012;48:1751-6. [Crossref] [PubMed]
- Sauerbrei W, Royston P, Look M. A new proposal for multivariable modelling of time-varying effects in survival data based on fractional polynomial time-transformation. Biom J 2007;49:453-73. [Crossref] [PubMed]
- Bolard P, Quantin C, Esteve J, et al. Modelling time-dependent hazard ratios in relative survival: application to colon cancer. J Clin Epidemiol 2001;54:986-96. [Crossref] [PubMed]
- Bellera CA, MacGrogan G, Debled M, et al. Variables with time-varying effects and the Cox model: some statistical concepts illustrated with a prognostic factor study in breast cancer. BMC Med Res Methodol 2010;10:20. [Crossref] [PubMed]
- Cormier JN, Huang X, Xing Y, et al. Cohort analysis of patients with localized, high-risk, extremity soft tissue sarcoma treated at two cancer centers: chemotherapy-associated outcomes. J Clin Oncol 2004;22:4567-74. [Crossref] [PubMed]
- Fontein DBY, Klinten Grand M, Nortier JWR, et al. Dynamic prediction in breast cancer: proving feasibility in clinical practice using the TEAM trial. Ann Oncol 2015;26:1254-62. [Crossref] [PubMed]
- Rueten-Budde AJ, van Praag VM, van de Sande MAJ, et al. Dynamic prediction of overall survival for patients with high-grade extremity soft tissue sarcoma. Surg Oncol 2018;27:695-701. [Crossref] [PubMed]
(English Language Editor: A. Kassem)


