Polarized photoacoustic microscopy based on high-order harmonics for anisotropy detection

Tao Wang; Jun Yang; Wensai Wang; Lingxiao Wang; Xiaochun Wang; Sheng Zhou

doi:10.21037/atm-22-794

Original Article

Polarized photoacoustic microscopy based on high-order harmonics for anisotropy detection

Tao Wang, Jun Yang, Wensai Wang, Lingxiao Wang, Xiaochun Wang, Sheng Zhou

Chinese Academy of Medical Sciences & Peking Union Medical College, Institute of Biomedical Engineering, Tianjin, China

Contributions: (I) Conception and design: T Wang; (II) Administrative support: J Yang; (III) Provision of study materials or patients: J Yang; (IV) Collection and assembly of data: T Wang; (V) Data analysis and interpretation: T Wang; (VI) Manuscript writing: All authors; (VII) Final approval of manuscript: All authors.

Correspondence to: Jun Yang. Chinese Academy of Medical Sciences & Peking Union Medical College, Institute of Biomedical Engineering, Tianjin, China. Email: Yangj3210@hotmail.com.

Background: Anisotropy which encodes rich structure and function information is one of the key and unique characteristics of tissues. Polarized photoacoustic imaging shows tremendous potential for the detection and quantification of the anisotropy of tissues. The existing polarized photoacoustic imaging methods cannot quantify anisotropy and detect the orientation of the optical axis in 3D imaging.

Methods: We proposed a versatile polarized photoacoustic imaging method based on the detection of high-order harmonics of the photoacoustic signal, which can be used for both 2D and 3D polarized photoacoustic imaging, This method can detect and quantify the anisotropy and the orientation of the optical axis of the anisotropic objects by the amplitude and initial phase of the high-order harmonics. A double-focusing polarized photoacoustic microscopy was developed to validate the proposed method. Experiments were conducted on 2D and 3D anisotropic phantoms.

Results: The results showed that the anisotropy and the orientation of the optical axis of the anisotropic object can be detected and quantified accurately by the amplitude and initial phase of the high-order harmonics, even at a depth of triple transport mean free path. The imaging depth of the polarized photoacoustic microscopy is mainly limited by laser energy attenuation rather than depolarization.

Conclusions: Polarized photoacoustic microscopy based on high-order harmonics has tremendous potential for imaging the anisotropy of deep biological tissues in vivo. It also extends the capability of photoacoustic microscopy to image the anisotropy of tissues.

Keywords: Anisotropy; high-order harmonic; polarized photoacoustic microscopy

Submitted Jan 12, 2022. Accepted for publication Mar 01, 2022.

doi: 10.21037/atm-22-794

Introduction

Anisotropy refers to the directional dependence of physical properties of a material or that the particular property of interest differs when measured across different axes. Anisotropy is a key and unique characteristic of tissues (1). Several tissues exhibit anisotropy, including skin, cornea, sclera, cartilage, and other connective tissues (2). The anisotropy structure is crucial for the mechanical stability, elasticity, and functioning of tissues and organs. Indeed, collagen fibrils in sclera cannot transmit light owing to their random size and arrangement, whereas the cornea shows transparency owing to its polycrystalline lattice structure (3). The anisotropic architecture of the tissue alteration can cause serious conditions such as Ehlers-Danlos syndrome, glaucoma, and alpha-2-deficient collagen disease (4). Certain alterations will even remodel the extracellular matrix, which in turn influences the course and progression of several other pathological conditions, including fibrosis, skin disorders, and cancer (5). Therefore, anisotropy encodes rich structural and functional information, besides being important for diagnosing certain specific diseases.

The detection of the anisotropy of tissues remains a challenge. Several techniques have been employed to address this problem, including small-angle light scattering (SALS) (6), X-ray scattering (7), second harmonic generation microscopy (SHG) (8), polarization sensitive optical coherence tomography (PS-OCT) (9), and polarized light microscopy (PLM) (10). Besides these techniques being useful, some of them can even achieve sub-micron resolution. Several of these techniques have delivered promising results, such as detecting the collagen fiber structure of the cornea and sclera. However, all of these techniques have one or more limitations. For example, most of these techniques require chemical processing and sectioning of tissues, which is highly invasive and can damage the original structure of the tissues (11). Consequently, these techniques can rarely achieve in vivo imaging. Furthermore, certain techniques such as SHG are only sensitive to a few specific tissues (12). Other birefringence-based techniques, such as SALS, suffer from limitations in imaging depth (13). Hence, it is preferable to develop a non-invasive technique to detect anisotropic architecture in deep tissues.

Photoacoustic imaging, which is a non-invasive imaging technique that combines both the high resolution of optical imaging and the penetration depth of ultrasound imaging, has been extensively studied. However, in most photoacoustic imaging systems, the anisotropy of the tissues and the polarization state of light are not considered. The concept of dichroism-sensitive photoacoustic imaging was first proposed by Hu et al. (14). They pointed out that photoacoustic imaging has certain advantages in detecting dichroism contrasts of biomolecules and can eliminate the background of non-anisotropy. Thereafter, only a few works on polarized photoacoustic imaging have been reported, and the imaging methods of these works vary. These imaging methods are effective in certain cases, though with certain limitations. Direct usage of photoacoustic imaging, acquired at a different polarization angle of the incident linearly polarized light, cannot quantify the anisotropy and detect the orientation of the optical axis of the targets. Imaging methods based on modulating the polarization angle of the incident linearly polarized light require a plethora of photoacoustic images (15). Other imaging methods based on the concept of the degree of anisotropy (DOA) exclude the factor of energy attenuation following the passing of the light through the anisotropic targets, and hence they are only suitable for 2D imaging (16).

We have analyzed the photoacoustic effect of 2D and 3D anisotropic targets generated by linear polarized light in detail, and a versatile polarized photoacoustic imaging method based on the detection of the high-order harmonics of the photoacoustic signal has been proposed. This imaging method can be employed to distinguish the anisotropic targets in both 2D and 3D polarized photoacoustic imaging. It can also quantify the anisotropy and detect the orientation of the optical axis of the targets. Furthermore, double-focusing polarized photoacoustic microscopy has been developed. Experiments conducted on the 2D and 3D anisotropic phantoms verified the effectiveness of the proposed method. The anisotropy and the orientation of the optical axis of the anisotropic objects can be detected and quantified precisely by the amplitude and initial phase of the high-order harmonics, even at a depth of triple transport mean free path. Polarized photoacoustic microscopy based on high-order harmonics has tremendous potential for imaging the anisotropy of deep biological tissues in vivo. It also extends the capability of photoacoustic microscopy to image the anisotropy of tissues.

Methods

Theory

When an object is irradiated by a pulse laser with a polarization angle of $ϕ$ , the amplitude of the photoacoustic signal $P A (\vec{r}, ϕ)$ induced by the photoacoustic effect in the imaging plane is a function of the spatial position $\vec{r}$ of the object and the polarization angle $ϕ$ of the laser. Specifically, $P A (\vec{r}, ϕ)$ is proportional to the absorption coefficient of object $μ_{a} (\vec{r}, ϕ)$ , and the local laser energy deposition $F (\vec{r}, ϕ)$ is given below as

$P A (\vec{r}, ϕ) \propto μ_{a} (\vec{r}, ϕ) F (\vec{r}, ϕ)$ [1]

For polarized photoacoustic imaging, it is necessary to consider the anisotropy of the object. The absorption coefficient is different when the polarization angle of the laser is perpendicular or parallel to the optical axis of the anisotropic object. Thus, the absorption coefficient $μ_{a} (\vec{r}, ϕ)$ in Eq. [1] needs to be converted into the absorption coefficient along the polarization angle of the laser as

$μ_{a} (\vec{r}, ϕ) = μ_{a ⊥} (\vec{r}) \frac{n^{3} (\vec{r}, ϕ)}{n^{3}_{⊥} (\vec{r})} \cos^{2} (ϕ - θ (\vec{r})) + μ_{a ∥} (\vec{r}) \frac{n^{3} (\vec{r}, ϕ)}{n^{3}_{⊥} (\vec{r})} \sin^{2} (ϕ - θ (\vec{r}))$ [2]

where $θ (\vec{r})$ is the angle of the optical axis at position $\vec{r}$ in the object, and $n (\vec{r}, ϕ)$ , $n_{⊥} (\vec{r})$ , and $n_{∥} (\vec{r})$ are the real parts of the refractive index along the polarization direction, perpendicular to the optical axis, and parallel to the optical axis, respectively. The terms $μ_{a_{⊥}} (\vec{r})$ and $μ_{a ∥} (\vec{r})$ are the absorption coefficients, perpendicular and parallel to the optical axis, respectively. For several anisotropic objects, the refractive index changes $Δ n / \bar{n} = (n_{⊥} - n_{∥}) / (\frac{n_{⊥} + n_{∥}}{2})$ are miniscule in both directions, perpendicular and parallel to the optical axis. We assume that $n (\vec{r}, ϕ) \approx n_{⊥} (\vec{r}, ϕ) \approx n_{∥} (\vec{r}, ϕ)$ , and the Eq. [2] can be simplified as

$\begin{array}{l} μ_{a} (\vec{r}, ϕ) = μ_{a, ⊥} (\vec{r}) \cos^{2} (ϕ - θ (\vec{r})) + μ_{a, ∥} (\vec{r}) \sin^{2} (ϕ - θ (\vec{r})) \\ = \frac{μ_{a, ⊥} (\vec{r}) + μ_{a, ∥} (\vec{r})}{2} + \frac{μ_{a, ⊥} (\vec{r}) - μ_{a, ∥} (\vec{r})}{2} \cos (2 (ϕ - θ (\vec{r}))) \\ = μ_{a} (\vec{r}) [1 + \frac{Δ μ_{a} (\vec{r})}{2 \bar{μ_{a}} (\vec{r})} \cos (2 (ϕ - θ (\vec{r})))] \end{array}$ [3]

where $Δ μ_{a} (\vec{r}) = μ_{a, ⊥} (\vec{r}) - μ_{a, ∥} (\vec{r})$ is the variation of the absorption coefficient, representing the anisotropy of the object, and $μ_{a} (\vec{r}) = \frac{μ_{a, ⊥} (\vec{r}) + μ_{a, ∥} (\vec{r})}{2}$ is the average of the absorption coefficient. If the linear polarized laser with a polarization angle $ϕ$ has been obtained from a circular polarized laser, which implies that the laser fluence is the same at all polarization angles, then $F (\vec{r}, ϕ)$ can be replaced with $F (\vec{r})$ and the Eq. [1] can be rewritten as

$F A (\vec{r}, ϕ) \propto \bar{μ_{a}} (\vec{r}) F (\vec{r}, ϕ) [1 + \frac{Δ μ_{a} (\vec{r})}{2 \bar{μ_{a}} (\vec{r})} \cos (2 (ϕ - θ (\vec{r})))]$ [4]

We find that the amplitude of the photoacoustic signal oscillates with the polarization angle of the laser when the anisotropic object is illuminated by a linear polarized laser. However, when the isotropic object is illuminated by the linear polarized laser, the absorption coefficient of the isotropic object is $μ_{a} (\vec{r}, ϕ) = \frac{μ_{a, ⊥} (\vec{r}) + μ_{a, ∥} (\vec{r})}{2} = μ_{a, ⊥} (\vec{r}) = μ_{a, ∥} (\vec{r})$ , and $\nabla μ_{a} (\vec{r})$ in Eq. [4] becomes zero. The absorption coefficient of the isotropic object is independent of the polarization angle of the laser, and the amplitude of the photoacoustic signal is a constant. Hence, for 2D polarized photoacoustic imaging, the absence of the second harmonic term can be utilized for distinguishing and determining the anisotropy of the object. The anisotropy can be quantified by detecting the intensity of the second harmonic term. The initial phase $θ (\vec{r})$ describes the optical axis direction angle, and this can be used to detect the optical axis direction of the uniaxial object such as the orientation of a collagen fiber.

For 3D polarized photoacoustic imaging, we suppose that an object is composed of n layers, as shown in Figure 1.

Figure 1 Photoacoustic signal generated by the linearly polarized laser at different layers. The yellow arrow indicates the polarization angle of the laser, and the white arrow indicates the orientation of the optical axis. PA, photoacoustic.

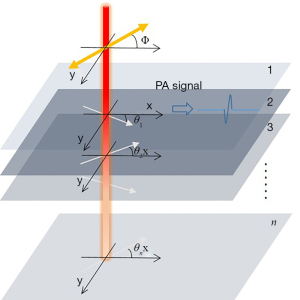
The absorption coefficients for the directions parallel and perpendicular to the optical axis of each layer are $μ_{n, ∥}$ and $μ_{n, ⊥}$ , respectively. The angle of the optical axis of each layer is $θ (n)$ , and the polarization angle of the incident laser is $ϕ$ , besides its rotation at a frequency f. F(n) is the laser energy at layer n, and the amplitude of the photoacoustic signal at layer n is $P A (n, ϕ)$ . The amplitude of the photoacoustic signal generated by the linear polarized laser has been introduced to simplify the formula. The terms $\frac{μ_{n, ⊥} + μ_{n, ∥}}{2}$ and $\frac{μ_{n, ⊥} - μ_{n, ∥}}{2}$ are simplified as a_n and b_n, respectively, and then the amplitude of the photoacoustic signal at the first and second layer are as shown in Eq. [5] and Eq. [6]. The amplitude of the photoacoustic signal at the first layer is identical to the 2D polarized photoacoustic imaging. However, for the second layer, owing to the absorption, the local fluence at the second layer can be expressed as $F (2) = F (1) [1 - a_{1} - b_{1} \cos 2 (ϕ - θ (1))]$ , and then the amplitude of the photoacoustic signal at the second layer can be expressed as

$P A (1, ϕ) \propto F (1) [a_{1} + b_{1} \cos 2 (ϕ - θ (1))]$ [5]

$P A (2, ϕ) \propto F (2) [a_{2} + b_{2} \cos 2 (ϕ - θ (2))]$ [6]

$P A (2, ϕ) \propto F (1) [\begin{array}{l} a_{2} - a_{1} a_{2} - a_{2} b_{1} \cos (2 ϕ - 2 θ (1)) + (1 - a_{1}) b_{2} \cos (2 ϕ - 2 θ (2)) \\ - \frac{b_{1} b_{2}}{2} (\cos (4 ϕ - 2 θ (2) - 2 θ (1)) + \cos (2 θ (1) + 2 θ (2))) \end{array}]$ [7]

As shown in Eq. [7], if both the first and second layer are anisotropic, then a high-order harmonic term at 4f besides the fundamental modulation frequency of 2f has occurred in the photoacoustic signal at the second layer. The absence of the high-order harmonic term can be utilized to distinguish the anisotropy of the second layer. Furthermore, the initial phase in the high-order harmonic term is the sum of the optical axis angles of the first and second layers, and this can be used to detect the optical axis of the second layer. The intensity of the high-order harmonic term is the product of the variation of absorption coefficient at the first and second layer, and this can be used to characterize the anisotropy of the second layer.

For the amplitude of the photoacoustic signal at the n_th layer, it is easy to deduce the following

$\begin{array}{l} P A (n, ϕ) \propto F (n) [a_{n} + b_{n} \cos 2 (ϕ - θ (n))] \\ = F (n - 1) [1 - a_{n - 1} - b_{n - 1} \cos 2 (ϕ - θ (n - 1))] [a_{n} + b_{n} \cos 2 (ϕ - θ (n))] \end{array}$ [8]

When the laser passes through an anisotropic layer, the multiplication of the oscillatory term will produce a high-order harmonic term, which results in a unique term with a frequency 2nf. Therefore, the absence of frequency 2nf can be used to distinguish the anisotropic and isotropic objects at the n_th layer. The initial phase of the high-order harmonic can be utilized to detect the optical axis of the n layer. The intensity of the high-order harmonic term can be used to characterize the anisotropy of the n_th layer.

Experimental setup

A diagram of the polarized photoacoustic microscopy system is shown in Figure 2, and the laser source is a pulsed Q-switched laser (Model AO-L-1064-II, Changchun New Industries Optoelectronics Technology Inc., Changchun, China) with 1 kHz repetition rate. The output of the laser is an elliptically polarized laser (as per inset 1 indicated in Figure 2). The laser beam is first frequency doubled, hence the wavelength of the laser beam is 532 nm. Then, the laser beam passes through a spatial filter, which is composed of 2 plano-convex lenses and an iris to collimate and adjust the beam size. The collimated laser is sampled by a beam sampler (BS), and a part of the laser is recorded by the photodetector (PD) for compensating the fluctuation of the laser energy. Thus, the major part of the laser passes through the first Gelan-polarizer (GT-P1) and quarter wave plate (QWP) to obtain a circular polarized laser (as per inset 3 indicated in Figure 2). The circular polarized laser then passes through the second Gelan-polarizer (GT-P2). The circular polarized laser is transformed to a linear polarized laser (as per inset 2 indicated in Figure 2). By rotating the Gelan-polarizer, a linear polarized laser beam with a different polarization angle, but similar energy, can be obtained. The linear polarized laser is then reflected by a mirror and passes through 2 axicons, which change the laser orientation and reshape the circular beam to an annular beam. Finally, the annular beam focuses on the sample surface by a costumed plano-convex lens with a central hole. A single element concave transducer, with a central frequency of 50 MHz and 80% bandwidth of the transducer, is placed in the hole. The transducer collects the photoacoustic signal and then amplifies it by a costumed amplifier. The amplified photoacoustic signal is sampled by a data acquisition card (Model QT1144, Queentest Inc., Beijing, China) and processed by the computer.

Figure 2 Diagram of the polarized photoacoustic microscopy system. The inset represents the angle dependence of laser intensity at 1, 2, and 3 positions. BS, beam sampler; GT-P1, the first Gelan-polarizer; QWP, quarter wave plate; GT-P2, the second Gelan-polarizer; PD, photodetector; AMP, amplifier; DAQ, data acquisition card.

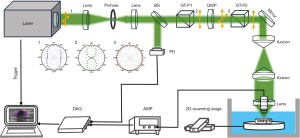
The GT-P2 is driven by a stepper motor. The samples are driven by a 2D scanning stage. Before the image acquisition process, by adjusting the focal zone of the transducer and the laser beam focus confocal, the polarized photoacoustic microscopy system can work on the optical resolution for the 2D polarized photoacoustic imaging. By adjusting the focal zone of the transducer below the laser beam focus, the polarized photoacoustic microscopy system can work on the acoustic resolution for the 3D polarized photoacoustic imaging. During the image acquisition process, point-by-point raster scanning is performed by the 2 linear translation stages. For each point, a series of photoacoustic A-lines at different polarization angles are acquired and finally reconstructed to a sequence of images at different polarization angles. The laser fluence is less than 0.5 mJ/cm², much below the American National Standards Institute safety limit.

Statistical analysis

The amplified photoacoustic signal is sampled by a data acquisition card (Model QT1144, Queentest Inc., Beijing, China) and processed by the computer.

Results

2D phantom imaging by the polarized photoacoustic microscopy system

To verify the theory of 2D polarized photoacoustic imaging, a 2D phantom made from linear polarizers and silicone rubber were imaged. Linear polarizers have served as useful anisotropic phantoms in previous work. Silicone rubber has also been imaged as an isotropic phantom. Figure 3A is the image of the phantom, where 2 linear polarizers were placed perpendicular to each other, and the silicone rubber was placed near the linear polarizer. Both the linear polarizers and the silicone rubber were embedded in agar gels (1.5% agar in distilled water). During the data acquisition process, the photoacoustic image was acquired at every 15° interval, ranging from 0° to 705°, and 48 photoacoustic images were acquired in total.

Figure 3 2D anisotropy phantom result. (A) Image of the linear polarizer and silicone rubber phantom. (B) Image sequences of the phantom acquired by the polarized photoacoustic system. (C) Normalized photoacoustic amplitude as a function of the relative polarized angle of the excited laser at represented positions A, B, and C marked by red rectangles in (A). (D) Spectrum of the normalized photoacoustic signal at represented positions A, B, and C. (E) Second-harmonic frequency image reconstructed from the amplitude of the spectrum at frequency f=2. (F) Color-coded optical axis orientation image of the phantom. (G) DOA image of the phantom. LP, linear polarizer; SR, silicone rubber; PA, photoacoustic; DOA, degree of anisotropy.

Figure 3B shows parts of the polarized photoacoustic microscopy images acquired at different polarization angles, and the number above the image is the relative polarization angle of the linearly polarized laser excited on the phantom. As shown in the image sequence, the photoacoustic signal intensity of the silicone rubber was greater than that of the polarizer. However, the photoacoustic signal intensity of the polarizer changed with the polarization angle of the incident laser, whereas the silicone rubber remained unchanged. By selecting representative positions of the polarizer and silicone rubber, as per the red rectangles marked in Figure 3A, we took the photoacoustic signal intensity of these pixels as a function of the relative polarization angle of the incident laser. The curve of the function is shown in Figure 3C. According to Figure 3C, the photoacoustic signal intensity of the polarizer changed with the relative polarization angle of the incident laser by following a sinusoidal law, since the polarizer is anisotropic and its absorption coefficient changes with the polarization angle of the incident laser. However, the silicone rubber is isotropic and its absorption coefficient will not alter with the polarization angle of the incident laser. The result is consistent with the 2D polarized photoacoustic imaging theory given in the “Methods” section.

In this experiment, the period of the polarization angle was 2π. The sample frequency was taken as 24, by assuming that the polarization of the laser beam has a frequency f=2. According to the Fourier spectrum of the normalized photoacoustic signal as shown in Figure 3D, there was an obvious peak at f=2 in the spectrum, which was twice the frequency of the polarization angle of the incident laser. The spectrum of the photoacoustic signal of the silicon rubber was near zero at f=2. The initial phase of the 2 polarizers had a phase difference of π/2 at f=2, since the 2 polarizers were placed perpendicularly, and their optical axis angles differed by 90°. By calculating the spectrum and initial phase from the image sequences of polarized photoacoustic microscopy, pixel by pixel, the second-harmonic frequency image was reconstructed from the amplitude of the spectrum at frequency f=2, as shown in Figure 3E. The linear polarizers were much more prominent when compared with the image sequences of polarized photoacoustic microscopy, whereas the silicon rubber in the second-harmonic frequency image was invisible. The intensity of each pixel of the linear polarizer was basically proximate to 1, since the materials of the 2 polarizers and the anisotropy of the 2 polarizers were the same. The intensity ratio of the linear polarizers to the silicone rubber was approximately 26.2 dB. Figure 3F is the color-coded optical axis orientation image reconstructed from the initial phase at frequency f=2.

According to the definition of DOA,

$D O A = \sqrt{Q_{P A}^{2} + U_{P A}^{2}} / I_{P A}$ [9]

where $Q_{P A} = I_{H - P A} - I_{V - P A}$ , $U_{P A} = I_{P}_{- P A} - I_{M - P A}$ , and $I_{P A} = I_{H - P A} + I_{V - P A}$ . $I_{H - P A}$ , $I_{V - P A}$ , $I_{P - P A}$ , and $I_{M - P A}$ are the amplitudes of the photoacoustic signal when the polarization angle of the laser is 0°, 90°, 45°, and 135° (16), respectively. We reconstructed the DOA image from the photoacoustic images acquired at 0°, 90°, 45°, and 135°. According to Figure 3G, owing to the strong anisotropy of the linear polarizer, the DOA of the linear polarizer was close to 1, whereas the silicon rubber was almost zero. However, there were certain artifacts in the DOA image. Part of the silicon rubber was still visible in the DOA image, and the DOA value of each pixel on the linear polarizer had an obvious difference.

3D phantom imaging by the polarized photoacoustic microscopy system

To verify the theory of 3D polarized photoacoustic imaging, a 3D phantom, made from 3 thin linear polarizers, were imaged. Figure 4A is the image of the phantom. The 3 linear polarizers were at different orientations and fixed at different depths in the agar gel. During data acquisition, the photoacoustic images were acquired at every 5°, ranging from 0° to 715°, and 144 photoacoustic images were acquired in total. Figure 4B is the 3D photoacoustic image which was reconstructed from the photoacoustic image, acquired at 0°, 45°, 90°, and 135°. The photoacoustic signal intensity of each of the linear polarizers changed with the polarization angle of the incident laser.

Figure 4 3D anisotropy phantom. (A) Image of the phantom. (B) 3D photoacoustic image sequences of the phantom acquired by the polarized photoacoustic system.

Figure 5A,5B show the photoacoustic signal intensity of the 3 linear polarizers. A, B, C, D, and E are the 5 representative pixels selected at different positions of the 3 linear polarizers. A, D, and E were selected from the non-overlapping areas on the first-, second-, and third-layer linear polarizer, respectively. B and C are the pixels from the overlapping areas on the second- and third-layer linear polarizer, respectively. According to Figure 5A, since the 3 polarizers were made of the same material, the amplitude and frequency of the photoacoustic signal were basically identical to those of the non-overlapping area. The major difference was the initial phase, since the optical axis of each linear polarizer was different. Nevertheless, for the photoacoustic signal at the overlapping area, the variation of the photoacoustic signal with polarization angle was very complex, and the photoacoustic signals were still periodic signals. However, the frequency components of the photoacoustic signals were complex, which is different from the non-overlapping area.

Figure 5 Analysis of representative point in 3D anisotropy phantom. (A) Normalized photoacoustic amplitude at the non-overlapping area. (B) Normalized photoacoustic amplitude at the overlapping area. (C) Spectrum of the normalized photoacoustic amplitude at the non-overlapping area. (D) Spectrum of the normalized photoacoustic amplitude at the overlapping area. PA, photoacoustic.

Figure 5 shows the Fourier spectrum of the normalized photoacoustic signal at different positions on the linear polarizer. For the non-overlapping area, the Fourier spectrum is shown in Figure 5C. There was only 1 obvious peak at frequency f=2 in the spectrum, and the amplitude of the peak was basically the same. For the overlapping area, the Fourier spectrum is shown in Figure 5D. The spectrum shows 2 peaks at frequencies f=2 and f=4 for the overlapping area on the second linear polarizer layer. For the overlapping area on the third linear polarizer layer, the spectrum shows 3 peaks at frequencies f=2, f=4, and f=6, which were exactly 2, 4, and 6 times that of the polarization angle frequency of the incident laser, respectively.

Figure 6 shows the 3D high-order harmonic images. As shown in Figure 6A, all 3 linear polarizers were visible in the 3D high-order harmonic images reconstructed from the amplitude of the spectrum at frequency f=2, though the intensity of the non-overlapping area was much stronger than that of the overlapping area. Figure 6B is the 3D high-order harmonic image reconstructed from the amplitude of the spectrum at frequency f=4, and the non-overlapping area was removed. Figure 6C is the 3D high-order harmonic image reconstructed from the amplitude of the spectrum at frequency f=6, and only the overlapping area on the third layer was visible. These results are consistent with the 3D polarized photoacoustic imaging theory given in the “Methods” section.

Figure 6 3D high-order harmonic images. (A) Reconstructed from the amplitude of the spectrum at frequency f=2. (B) Reconstructed from the amplitude of the spectrum at frequency f=4. (C) Reconstructed from the amplitude of the spectrum at frequency f=6.

Discussion

The phantom experiment, which uses polarized photoacoustic imaging based on the detection of the high-order harmonics of the photoacoustic signal, is a useful technology to characterize anisotropy and detect the optical axis. For 2D polarized photoacoustic imaging, both the DOA image and second harmonic frequency image can highlight the anisotropic object and eliminate the isotropic background. Furthermore, both the DOA and the amplitude of the second harmonic frequency can quantify anisotropy. However, the second harmonic frequency image is more robust than the DOA image. A small value of I_PA could result in a large DOA value. Additionally, the optical axis can be obtained by calculating the initial phase of the second harmonic frequency, while the DOA image cannot.

For 3D polarized photoacoustic imaging, the photoacoustic signal of the superficial object is identical to that of 2D polarized photoacoustic imaging. However, for the object under the anisotropic material, since both the absorption coefficient and the local fluence oscillate with the polarization angle, the multiplication of the absorption coefficient and the local fluence induce the high-order harmonics term in the photoacoustic signal. The frequency component of the photoacoustic signal becomes increasingly complex for more of the anisotropic material that the linear polarized laser passes through. Owing to the complex frequency component of the photoacoustic signal, directly using DOA to distinguish and quantify anisotropy will produce a wrong result. Thus, the anisotropy of the object under the anisotropic material can only be distinguished and quantified by a high-order harmonic. Moreover, the high-order harmonics image can be employed to estimate the number of layers of the anisotropic material that the linearly polarized laser has passed through prior to reaching the position.

We used the polarization angle of the linearly polarized laser in this experiment as the relative angle. Hence, the calculated optical axis direction of the anisotropic object is also the relative angle, and the absolute angle of the optical axis can be obtained by replacing the polarization angle of the linearly polarized laser with an absolute angle.

Polarized photoacoustic imaging obtains the material anisotropy and optical axis from the photoacoustic signal intensity. The imaging contrast depends on the linear dichroism of material, which is different from certain traditional methods such as polarization microscopy and polarization OCT. Most of these technologies depend on the linear birefringence of the material, and these technologies need to detect the light backscattering or the light passing through the material, which limits the imaging depth. Polarized photoacoustic imaging provides a more direct method, and its imaging depth depends on the energy attenuation and depolarization of the linear polarized transmission in the object. We aimed to assess the imaging depth of polarized photoacoustic microscopy. The depolarization of the incident linear polarized lasers and the photoacoustic signal amplitude of a linear polarizer after the passing of the scattering phantoms with different thickness were tested. The scattering phantom was made by 3% agar and 0.25% intralipid in distilled water. The transport mean free path of the phantom was ~4 mm (15).

The experimental setup for detecting the depolarization of the incident linear polarized laser is shown in Figure 7A. Figure 7B demonstrates that the linearly polarized laser gradually becomes an unpolarized laser with the increase of the thickness of the phantom. According to Figure 7C, both the photoacoustic signal and the degree of the linear polarization (DLP) of the lasers are reduced with the phantom thickness. The amplitude of the second harmonic also reduces with the phantom thickness. However, the attenuation of the energy is faster than the depolarization of the laser. Figure 7C shows that the effective imaging depth is estimated to be about triple transport mean free path. However, this is primarily due to the energy attenuation. A deeper imaging depth can be achieved by enhancing the laser energy for the time period that the laser can maintain sufficient DLP. These results are consistent with certain research published by other groups. Therefore, for the imaging of deep tissue, polarized photoacoustic microscopy based on high-order harmonics has more advantages, and its image is reconstructed from acoustic signals. This makes it possible to realize in vivo imaging, unlike other methods such as polarization light microscopy, which require tissue slices. The polarized photoacoustic microscopy method provides an effective and straightforward strategy for tissue polarimetry, prefiguring great potential for biological imaging and material inspection.

Figure 7 Imaging depth measurement. (A) The experimental setup for detecting the depolarization of the linear polarized laser. (B) The polarization state of the laser after passing through the scattering phantoms. (C) The photoacoustic signal, the DLP of the lasers, and the amplitude of the second harmonic after passing the scattering phantoms. PD, photodetector; NoR.PA, normalized photoacoustic; DLP, degree of the linear polarization.

However, there are certain disadvantages of polarized photoacoustic imaging based on high-order harmonics. To obtain the high-order harmonic frequency of the photoacoustic signal, multiple photoacoustic images at different polarization angles need to be acquired. For the single-layer anisotropic material, according to the Nyquist sampling law, a minimum of 4 photoacoustic images at different polarization angles, ranging from 0 to π, need to be acquired. For 3D imaging, if the object consists of a multi-layer anisotropic material, the polarization angle of the incident laser needs to be subdivided more precisely while acquiring the data. In practice, the sampling rate usually needs to be several times higher than the Nyquist sampling frequency, and this will significantly increase the data acquisition time and the amount of data.

Conclusions

We have proposed a versatile polarized photoacoustic imaging method based on the detection of the high-order harmonics of the photoacoustic signal. This method can be applied for both 2D and 3D anisotropic object imaging. Polarized photoacoustic microscopy based on this method was designed. The effectiveness of the proposed imaging method and the polarized photoacoustic microscopy system was verified by imaging 2D and 3D phantoms. Compared with traditional imaging techniques, polarized photoacoustic microscopy based on high-order harmonics provides a more direct way to image anisotropic objects. The contrast of the polarized photoacoustic microscopy images originates from the anisotropy of the biological tissues, and the anisotropy information of the biological tissues was obtained from the photoacoustic signals. Owing to these advantages, polarized photoacoustic microscopy based on high-order harmonics has tremendous potential for imaging deep anisotropic biological tissues in vivo. Furthermore, it extends the capability of photoacoustic microscopy to image the anisotropy of tissues.

Acknowledgments

Funding: None.

Footnote

Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://atm.amegroups.com/article/view/10.21037/atm-22-794/coif). The authors have no conflicts of interest to declare.

Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.

References

Holmes DF, Lu Y, Starborg T, et al. Collagen Fibril Assembly and Function. Curr Top Dev Biol 2018;130:107-42. [Crossref] [PubMed]
Datta P, Vyas V, Dhara S, et al. Anisotropy properties of tissues: A basis for fabrication of biomimetic anisotropic scaffolds for tissue engineering. J Bionic Eng 2019;16:842-68. [Crossref]
Meek KM, Knupp C. Corneal structure and transparency. Prog Retin Eye Res 2015;49:1-16. [Crossref] [PubMed]
Kiss N, Fésűs L, Bozsányi S, et al. Nonlinear optical microscopy is a novel tool for the analysis of cutaneous alterations in pseudoxanthoma elasticum. Lasers Med Sci 2020;35:1821-30. [Crossref] [PubMed]
Arseni L, Lombardi A, Orioli D. From Structure to Phenotype: Impact of Collagen Alterations on Human Health. Int J Mol Sci 2018;19:1407. [Crossref] [PubMed]
Girard MJ, Dahlmann-Noor A, Rayapureddi S, et al. Quantitative mapping of scleral fiber orientation in normal rat eyes. Invest Ophthalmol Vis Sci 2011;52:9684-93. [Crossref] [PubMed]
Aghamohammadzadeh H, Newton RH, Meek KM. X-ray scattering used to map the preferred collagen orientation in the human cornea and limbus. Structure 2004;12:249-56. [Crossref] [PubMed]
Morishige N, Wahlert AJ, Kenney MC, et al. Second-harmonic imaging microscopy of normal human and keratoconus cornea. Invest Ophthalmol Vis Sci 2007;48:1087-94. [Crossref] [PubMed]
Yasuno Y, Yamanari M, Kawana K, et al. Visibility of trabecular meshwork by standard and polarization-sensitive optical coherence tomography. J Biomed Opt 2010;15:061705. [Crossref] [PubMed]
Jan NJ, Grimm JL, Tran H, et al. Polarization microscopy for characterizing fiber orientation of ocular tissues. Biomed Opt Express 2015;6:4705-18. [Crossref] [PubMed]
Jan NJ, Lathrop K, Sigal IA. Collagen Architecture of the Posterior Pole: High-Resolution Wide Field of View Visualization and Analysis Using Polarized Light Microscopy. Invest Ophthalmol Vis Sci 2017;58:735-44. [Crossref] [PubMed]
Chen X, Nadiarynkh O, Plotnikov S, et al. Second harmonic generation microscopy for quantitative analysis of collagen fibrillar structure. Nat Protoc 2012;7:654-69. [Crossref] [PubMed]
Quantock AJ, Winkler M, Parfitt GJ, et al. From nano to macro: studying the hierarchical structure of the corneal extracellular matrix. Exp Eye Res 2015;133:81-99. [Crossref] [PubMed]
Hu S, Maslov K, Yan P, et al. Dichroism optical-resolution photoacoustic microscopy. In: Biomedical Optics and 3-D Imaging, OSA Technical Digest. Washington, DC: Optica Publishing Group, 2012. doi: 10.1364/BIOMED.2012.BM2B.8.10.1364/BIOMED.2012.BM2B.8
Qu Y, Li L, Shen Y, et al. Dichroism-sensitive photoacoustic computed tomography. Optica 2018;5:495-501. [Crossref] [PubMed]
Zhang Z, Shi Y, Xiang L, et al. Polarized photoacoustic microscopy for vectorial-absorption-based anisotropy detection. Opt Lett 2018;43:5267-70. [Crossref] [PubMed]

(English Language Editor: C. Betlazar-Maseh)

Cite this article as: Wang T, Yang J, Wang W, Wang L, Wang X, Zhou S. Polarized photoacoustic microscopy based on high-order harmonics for anisotropy detection. Ann Transl Med 2022;10(6):293. doi: 10.21037/atm-22-794

Polarized photoacoustic microscopy based on high-order harmonics for anisotropy detection

Introduction

Methods

Theory

Experimental setup

Statistical analysis

Results

2D phantom imaging by the polarized photoacoustic microscopy system

3D phantom imaging by the polarized photoacoustic microscopy system

Discussion

Conclusions

Acknowledgments

Footnote

References

Article Options

Download Citation

Share