Univariate description and bivariate statistical inference: the first step delving into data

Introduction

When data are well prepared by using previously described methods such as correcting, recoding, rescaling and missing value imputation, the next step is to perform statistical description and inference (1,2). In observational studies, the first table is usually a display of descriptive statistics of overall population, as well as statistical inference for the difference between groups. This table is important in that it gives an estimate of the differences in baseline characteristics, and provides evidence for further multivariable analysis. The article first gives an overview of methods for bivariate analysis, and then provides a step-by-step tutorial on how to perform these analyses in R. Finally, I will show how to make the table automatically. This can be useful when there are a large number of variables.

Univariate description and bivariate statistical methods

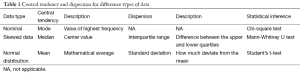
Varieties of methods are available for univariate description and bivariate inference. Table 1 displays central tendency and dispersion for different types of data. Mean and standard deviation are probably the most widely used statistics to describe normally distributed data. For skewed data, we employ median and interquartile range. For nominal data, mode can be used for description of central tendency. However, in practice we frequently describe it by the number of each category and relevant percentage. Student’s t test is typically applied when the test statistic would follow a normal distribution (3). Mann-Whitney U test is a non-parametric test that does not require assumption of normal distribution (4). For studies with multiple groups, analysis of variance (ANOVA) may be the best choice.

Table 1 Central tendency and dispersion for difference types of data
Full table

Working example

In the working example, I created three types of data that are most commonly encountered in practice. Nominal variables include those with multiple levels and those with two levels. Continuous variable include those with normal distribution and skewed data.

In this dataset, gender is a binomial variable that is assigned by “male” or “female”. Variable trt is also binomial, but it is used for grouping purpose. Variable diagnosis is categorical variable with four levels. Variable age is normally distributed with mean of 67 and standard deviation of 20. The last variable wbc is skewed in distribution. The last line combines these variables into a single data frame.

Examination of skewness and kurtosis

Because the choice of statistical methods depends on the distribution of data, the first step is to examine the skewness of data. The distribution can be visualized using histogram (Figure 1).

Figure 1 Histograms of variables of age and wbc. It appears that the distribution of age was symmetrical, while the variable wbc is skewed.

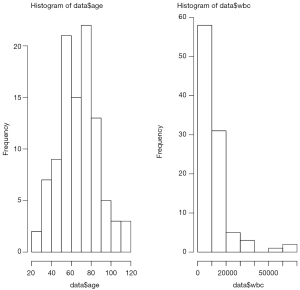
The first line called par() function to dictate that subsequent figures will be drawn in 1×2 array. It is for the purpose of better visualization and users can omit it in their own practices. As we can see from Figure 1, the distribution of age was symmetrical, while the variable wbc is skewed. However, graphic visualization only gives a hint on the distribution of data. To make formal judgment, we need statistical tests. The package moments provides good functions to do the task (5). Data distribution can be described by skewness and kurtosis. The former is a measure of the asymmetry of the probability distribution, and the latter is a measure of the “tailedness” of the probability distribution.

The package employs the D’Agostino skewness test, details of this method can be found in reference (6). The alternative hypothesis is that the data have a skewness. When P<0.05 as for the variable wbc, the alternative hypothesis is accepted and there is skewness.

Anscombe-Glynn kurtosis test is employed to test kurtosis (6,7). Data should have kurtosis equal to 3 under the hypothesis of normality. This test incorporates such null hypothesis and is useful to detect a significant difference of kurtosis in normally distributed data. As expected, the variable wbc has kurtosis that is significantly different from normality.

Univariate description

Since we know the distribution of data, we need to provide central tendency and dispersion in our research. Variable wbc will be expressed as median and interquartile range, and age will be expressed as mean and standard deviation. Other categorical variables will be expressed as number and percentage.

The above codes are used for description of overall cohort. We also want to describe variables separately by the treatment group.

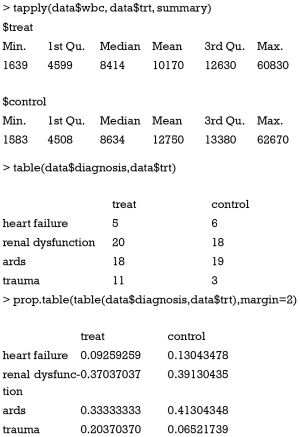
The function tapply() “applies a function to each cell of a ragged array, that is to each (non-empty) group of values given by a unique combination of the levels of certain factors.” (8). In our example, the function summary() is applied to variable wbc, stratified by treatment (trt). The results give summary values separately for each levels of the variable trt. The table() function is easy to use for cross tabulation.

Bivariate statistical inference

After univariate description, investigators can have a general impression on the effectiveness of a treatment. However, we still don’t know whether the difference is caused by random error, or there is a real difference. Varieties of sophisticated methods are designed to answer the question.

In above codes, the functions wilcox.test(), chisq.test() and t.test() are employed for skewed, categorical and normal data, respectively. The outputs of these functions include the name of the test, dataset, statistics and P value. These values can be assigned to an object for further use.

Making publication style table automatically

It is easy to copy and paste the above statistical outputs into a table in Microsoft Word when there are a limited number of variables. However, it is a tedious task when variables expand to dozens. Furthermore, making a blank table and input values by hand is prone to error. We may take the advantage of R that it allows for customized codes to automate the process of table making. It also allows to round number to desired decimal places.

Many journals require that description of a variable should be put in a single cell, thus we need to use character vector to store the output in the form like “mean ± SD”. The paste() function can connect mean and standard deviation by using the symbol “±”. The round() function is used to save only one decimal place. Skewed data can be store in a similar way.

This time I break the whole work into several pieces to make it clearer. The first line calculates the overall mean and standard deviation, and put them to a single cell. The second and third lines calculate the summary statistics for the treatment and control groups, respectively. Because not all summary statistics are wanted, we extracted the second, third and fifth values, which represent the first quartile, median and third quartile values. The last line combines all statistics into a character vector.

Next we need to combine all row variables into a matrix.

The matrix output appears nearly what we want. However, the column and row names are not exactly meet the requirements for submission. We can rename them easily. For the column name I added a new character vector so that each of the names can have a double quote.

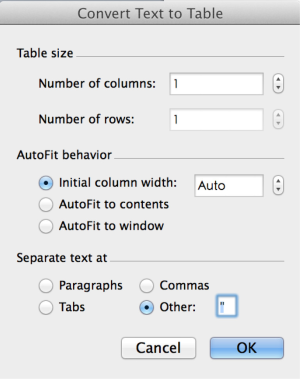
There are double quotes for each value, which is not the format for a publication quality table. The next task is done in Microsoft Word (MS). Users can copy the table from R console to MS and use the “convert text to table” function of the Word processor. In the “separate text at” option, you can use double quotes as the symbol to separate text. After click “OK” button, the double quotes mark will be replaced by lines forming cells of a table (Figure 2). Creating table in this way avoids you from copy and paste values one by one, which is less likely to make errors. Furthermore, because you have recorded every step for making the table in R code, you and others can reproduce the process. This is very important during revision. The rule of thumb in data management and statistical analysis is to make your results exactly reproducible.

Figure 2 Settings in Microsoft Word to convert text to table. Note that the double quote mark is used to separate text.

Summary

The article provides a gentle introduction to univariate statistical description and bivariate statistical inference, which is typically the first step in exploring data. Statistical description includes statistics for central tendency such as mode, mean, median. Dispersion includes standard deviation, range, and interquartile range. They are applied to different types of data. Also, there are several statistical inference methods. They are Student’s t-test, Mann-Whitney U test and Chi-square test. The results of these analyses should be put into a table for publication or conference presentation. The process can be automated by using R code, which makes the process easily reproducible by others and in subsequent revisions.

Acknowledgements

None.

Footnote

Conflicts of Interest: The author has no conflicts of interest to declare.

References

1. Zhang Z. Missing values in big data research: some basic skills. Ann Transl Med 2015;3:323.
2. Zhang Z. Data management by using R: big data clinical research series. Ann Transl Med 2015;3:303.
3. Fay MP, Proschan MA. Wilcoxon-Mann-Whitney or t-test? On assumptions for hypothesis tests and multiple interpretations of decision rules. Stat Surv 2010;4:1-39. [Crossref] [PubMed]
4. Corder GW, Foreman DI. Nonparametric statistics: A step-by-step approach. New York: Wiley, 2014.
5. Komsta L, Novomestky F. moments: moments, cumulants, skewness, kurtosis and related tests. 2012. R package version 0.13; 2014.
6. Ghasemi A, Zahediasl S. Normality tests for statistical analysis: a guide for non-statisticians. Int J Endocrinol Metab 2012;10:486-9. [Crossref] [PubMed]
7. DeCarlo LT. On the meaning and use of kurtosis. Psychological Methods 1997;2:292-307. [Crossref] [PubMed]
8. Breiman L. R. A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria, 2012. Machine Learning 2001;45:5-32. [Crossref] [PubMed]