
This article has an erratum available at: http://dx.doi.org/10.21037/atm-2022-47 the article has been update on 2022-08-09 at here.
Design and optimization of auditory prostheses using the finite element method: a narrative review
Introduction
Hearing mechanism and hearing loss
Auditory perception is how the ear transduces sound waves (vibration) into neural signals. Sound waves enter the outer ear and travel through the middle ear until reaching the inner ear, where hair cells convert the vibration information into neural signals. These signals ultimately reach the auditory cortex for perception (1). The complete auditory system consists of the peripheral and central auditory nervous systems, which is the basis for sound perception. The peripheral auditory system comprises the outer, middle, and inner ear. The outer ear comprises the pinna, ear canal, and tympanic membrane.
Moreover, the tympanic membrane separates the external ear canal from the middle ear. The middle ear includes the ossicular chain, tympanic cavity, and eustachian tube. The ossicular chain, which includes three ossicles (malleus, incus, and stapes), transmits the sound-induced vibrations of the tympanic membrane to the inner ear. The bony labyrinth in the inner ear mainly consists of the vestibule, three semicircular canals, and the coiled cochlea, which is filled with fluid (perilymph and endolymph). The movement of the stapes against the oval window (OW) creates waves in the cochlear fluid, which causes the basilar membrane (BM) to vibrate. The BM vibrations in turn produce motion in the sensory hair cells located in the organ of Corti, thereby stimulating nerve impulses for additional perception in the central auditory nervous system (2).
The central auditory nervous system spans the cerebral cortex of the brainstem, midbrain, and thalamus and is one of the most extensive central pathways in the sensory system. In the central auditory pathway, multiple parallel and overlapping pathways diverge and converge to deliver and analyze different information (3). The ascending auditory pathways achieve advanced processes by passing information to the auditory cortex, which generates conscious perception. In contrast, most of the information carried by the auditory descending pathways is inhibitory. As shown in Figure 1, the entire process of hearing basically involves sound waves traveling through the ear, which eventually reach the central auditory nervous system for perception via some nerve fibers.
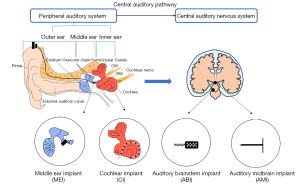
Any damage to the auditory system will result in hearing loss. For instance, damage to the ossicular chain interrupts vibration transmission and causes insufficient inner ear stimulation, which manifests as conductive deafness (4). Lesions in the cochlea or auditory central nervous systems present as sensorineural deafness with impaired sound perception. Mixed deafness occurs when two or more malfunctions coincide (5,6).
Auditory prostheses are devices that are implanted at lesion locations to restore hearing. For example, a middle ear implant (MEI) can be used for an individual with a middle ear disease coupled with ossicular chain damage (7) to reconstruct and repair functionality. A cochlear implant (CI) bypasses the damaged hair cells of the inner ear through direct electrical stimulation of the auditory nerves (8). If the lesion exists in the pathway from the cochlea to the auditory cortex, an auditory brainstem implant (ABI) and auditory midbrain implant (AMI) are considered (5,9-11). The ABI stimulates the cochlear nucleus in the brainstem, bypassing the auditory nerve, while an AMI stimulates the inferior colliculus. Furthermore, the CI, ABI, and AMI are electrode arrays of different sizes; CIs and AMIs are linear arrays, while the ABI is a two-dimensional (2D) array. Some typical auditory prostheses are shown in Figure 1, based on lesion locations.
Auditory prostheses design and optimization methods
There are some limitations to auditory prostheses after implantation. For example, long-term studies have demonstrated that dislocations and extrusions frequently appear after middle ear surgery (12), and residual hearing loss is severe after CI surgery (13,14). Many studies were devoted to optimizing middle ear prostheses. Common optimization parameters include the size, mass, and implant location of the implanted part (15-17). For inner ear prostheses, many parameters need to be optimized, such as the electrode length, electrodeposition, and coding strategy of CI (18-20).
Numerous designs and evaluation methods have been developed to optimize auditory prostheses, such as experiments on human temporal bones of cadavers (21-23), animals (24,25), and clinical volunteers (26). Animal and cadaveric experiments have determined parameters that influence hearing performance. However, it is challenging to conduct multiple experiments or optimize prostheses on specimens after implantation. Furthermore, animal and cadaveric experiments also require high-precision and complex instruments, such as laser Doppler vibrometry or phase Doppler interferometry, which are time-consuming and expensive. For instance, cadaveric experiments have been conducted on fresh human temporal bones by measuring tiny vibration stapes displacement with laser Doppler vibrometry to determine the effects of transducers on MEIs (27). Therefore, a convenient, low-cost, and repeatable method for prosthesis design and optimization is desirable. The finite element method (FEM) can meet these requirements and is carried out on the computer with substantial flexibility in terms of modifying different settings, such as the electrode shape and material.
Purpose and scope of the review
Some parameters of the auditory prosthesis, such as mass, implanted position, and degree, need to be repeatedly designed and optimized based on the realistic geometry of the ear. With the development of imaging and micro-measurement technologies, it has become possible to establish an accurate three-dimensional (3D) finite element (FE) model of the ear and the auditory prosthesis. Based on this 3D-FE model, the implanted components of the auditory prosthesis can be analyzed. This paper reviews the recent advances in the design and optimization of auditory prostheses using the FEM and provides suggestions for future development. We present the following article in accordance with the Narrative Review reporting checklist (available at https://atm.amegroups.com/article/view/10.21037/atm-22-2792/rc).
Methods
We searched PubMed and Web of Science for original research and review articles through 2022. Research terms include various combinations of “finite element method”, “ear”, “middle ear”, “inner ear”, “auditory prosthesis”, “cochlear implant”, “middle ear implant”, “hearing loss”. The literature on the design of auditory prostheses using the FEM has been extensively studied, including different types of ear models, relevant parameters of different auditory prostheses that need to be designed and optimized. Table 1 describes the study sequence and details.
Table 1
| Items | Specification |
|---|---|
| Date of search (specified to date, month and year) | 2021-6-30 to 2022-01-03 |
| Databases and other sources searched | PubMed and Web of Science |
| Search terms used (including MeSH and free text search terms and filters)* | “Finite element method”, “ear”, “middle ear”, “inner ear”, “auditory prosthesis”, “cochlear implant”, “middle ear implant”, “hearing loss” |
| Timeframe | 1989-10-01 to 2021-12-02 |
| Inclusion and exclusion criteria (study type, language restrictions, etc.) | Inclusion criteria: all references were found in PubMed and Web of Science and written in English |
| Selection process (who conducted the selection, whether it was conducted independently, how consensus was obtained, etc.) | Q Cheng, H Yu, Y Bai, G Ni collected and assembled the data. Then Q Cheng, H Yu, J Liu, Q Zheng conducted the classification and analysis of the information. Finally, all authors reached an agreement on the manuscript |
| Any additional considerations, if applicable | None |
*, an independent supplement table (Table S1) to present detailed search strategy from PubMed as an example.
FE models of the ear
In mathematics, the FEM is a numerical technique for solving approximate solutions to boundary value problems of partial differential equations. The FEM is analogous to the idea of connecting multiple tiny straight lines to approximate a circle. It regards the solution domain as consisting of many small interconnected sub-domains called FEs and assumes a suitable approximate solution to each element. The FEM in turn deduces and solves the general satisfaction conditions (such as the equilibrium conditions of the structure) to obtain the solution to the whole problem. It has high calculation accuracy and can be adapted to various complex shapes, making it an effective engineering analytical method for simulating physical systems.
The FEM can predict responses such as displacements, pressures, or voltage distribution in the complex auditory system (28). The FE model generally includes constructing geometry, meshing division, material property assignment, and boundary condition settings. FEM mesh is obtained by dividing a geometric model into many small units or elements. For 3D subjects, tetrahedra, hexahedra, and a combination are usually applied. There are numerous element types for researchers to select according to the research objective. For example, the mechanical element is needed to investigate the vibration of the ear, and electrical elements will be required when analyzing potential distribution in the cochlea. Assigning material properties, such as Young’s modulus or resistivity, is similar to element selection, depending on the analysis type. Different materials determine the different parameters of constitutive equations and can be used to calculate various results, such as mechanical displacement or voltage. The FEM has an apparent advantage in modeling biological systems with complicated structures, which are difficult for other methods such as the lumped parameters method (29,30).
Overall, the FE model can determine detailed responses at a target position of the simulated system. Compared with animal and clinical experiments, the geometry and material properties can be modified according to the design objective to facilitate repeated numerical experiments without equipment limitations. For example, a prosthesis can be integrated into some locations of an ear model to elicit mechanical or electrical responses, which can be used to find better implanted position by evaluating hearing responses (31,32).
Middle ear model
The middle ear model has been developed by including only a single tympanic membrane in a model and then gradually enriched to include the tympanic membrane, ossicular chain, and middle-ear cavity. The components of this model have become more abundant and detailed, including some soft tissues (33,34) and the external auditory canal (35-37), as shown in Figure 2.
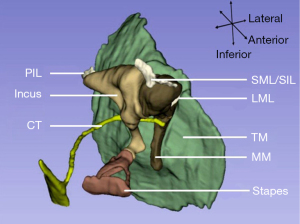
The geometry data for constructing models are often measured using a light microscope from the temporal bone sections at different angles with a rough spatial orientation. Laser scanning microscopy, with its higher resolution, can provide a more accurate geometry and has been used to measure the eardrum and ossicular chain. However, most measurements used to estimate the whole spatial locations of the middle ear are based on different specimens, resulting in some deviations (39). Another method that combines temporal bone histologic sections with computer-integrated 3D geometric reconstruction can improve the spatial accuracy of the ear model, such as the spatial location between three ossicles from the same specimen (40). In contrast, radiation-based imaging methods, magnetic resonance imaging, and computed tomography imaging are non-invasive and more suitable for living animals or human subjects. So that data for building ear models can be acquired clinically using imaging methods (41-44).
Inner ear model
The inner ear model often refers to the cochlear model, which can be simplified into two types: the box model and the spiral model. In the box model, the cochlea is straightened and includes the upper and lower cavities (scala vestibuli and scala tympani) separated by the BM. The arrangement of the spiral model is similar to the box model, but the geometry incorporates cochlea coiling (45,46).
Mechanical responses, such as the BM response, OW and round window (RW) volume velocity, and cochlear fluid pressure, can evaluate the inner ear performance. In addition to studying the mechanical response of the cochlea, some researchers have established volume conduction models to explore the electrical response of the cochlea (31,47-50). The volume conduction model differs from the mechanical model as it uses electrical characteristics, such as resistivity, to simulate each part of the ear (51). In this case, the inner ear model can calculate the electric field, current threshold, and local potential. In addition to these simplified models, more accurate and detailed structures of inner ear models have been developed, including the scalae (52,53), the organ of Corti (54,55), and coiling (56). Some studies also included auditory nerve fibers, which are located in the cochlear modiolus, to study neural response. Specifically, nerve fibers’ shape and starting position were simplified and then drawn along the cochlear modiolus to be integrated with the cochlear model. The neural response can then be presented as the potential distribution of the nerve fibers when conducting electrical analysis on the cochlea (57,58). However, a more complex model does not always provide a more accurate simulation; an appropriate model with relevant details should be constructed according to the research objective.
Whole ear model
Some studies of the inner ear model have applied mechanical stimulation on the OW to study the cochlear response (46,59). In some middle ear models, the cochlea was assumed as a mass, and stimulation was applied to the eardrum to study the middle ear transfer function (40,60-62). Other research has combined middle and inner ear models to study the responses during sound transmission by driving the tympanic membrane (63,64). The stimuli received by these partial models always estimate the external sounds and lack detailed interactions between the different structures from the outer ear to the inner ear. The ear canal and middle cavity are full of air, whereas the cochlea contains fluid, which increases the complexity of the sound transmission process. The whole ear model, which typically includes the ear canal, middle ear, and inner ear, can simulate a detailed sound transmission process and conduct investigations involving acoustic-structure-fluid coupling (28). Brown et al. studied blast wave transmission from the ear canal to the cochlea using a whole ear model and found that the organ of Corti might suffer substantial damage during blast exposure, reflecting the potential auditory injury (65). Although the whole ear model has some advantages, conducting an entire ear study in all ear-related research is unnecessary.
Models for auditory prostheses design and optimization
Models for middle ear prostheses
MEIs can be classified as wither passive or active. A passive MEI is used to reconstruct discontinuous or fixed ossicular chains without strengthening sound waves (66). Partial ossicular replacement prostheses (PORP), total ossicular replacement prostheses (TORP), and stapes prostheses are usually passive MEIs. On the other hand, an active MEI enhances sound waves through an external device before directly stimulating the middle ear components (67).
PORP and TORP
Middle ear prostheses affect the hearing response and thus auditory performance by changing the natural frequency of the ossicular chain (33). The PORP mainly connects the tympanic membrane or malleus handle to the stapes head, while the TORP links the tympanic membrane or malleus handle and the stapes footplate. The TORP can be used for reconstruction if the stapes arch is damaged or severely defective (12). Figure 3 displays situations when an ossicular replacement prosthesis is implanted into the middle ear.
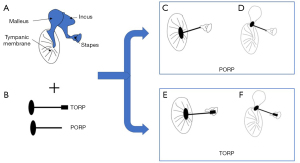
In many studies using the FEM to design and optimize ossicular replacement prostheses, the ossicle replacement prosthesis-induced vibration response of the stapedial footplate or tympanic membrane is regarded as a standard for evaluating the hearing performance of the prosthesis (68). Studies have found that some factors of the prosthesis, such as the geometry, implanting location, materials, and other parameters, are crucial to the performance of the prosthesis (15).
Specifically, an increase or decrease in the stiffness of the MEI affects the vibration amplitude (resonance/anti-resonance peak) of the stapes, too high stiffness of ossicular replacement prostheses will cause excessive stresses of the OW, too low stiffness will cause overlarge movement of resonance peak (34). Therefore, the stiffness of the MEI should match the natural frequency of the ossicular system, which may also help to explain the difference in the clinical manifestations of ossicular replacement surgery. The weight and implanted position of the prosthesis also influence the hearing response. The high stiffness and lightweight improve the efficiency of the incus replacement prosthesis. A PORP, located between the stapes head and the malleus manubrium or near the center of the tympanic membrane can induce a more significant stapes displacement, indicating better performance (69). Among three different contact positions (anterior, center, and posterior) of stapes footplate for a TORP, the footplate center achieved the best hearing recovery performance, providing a theoretical reference for selecting implant sites by surgeons (70). Therefore, the stiffness, mass, contact position, and interactions should be considered optimization factors during prosthesis design.
Stapes prosthesis
In addition to PORP and TORP, stapes prostheses have also been widely used. The only clinically available device is the piston prosthesis, which is commonly used in patients with conductive or mixed hearing loss due to stapes otosclerosis (71). This prosthesis consists of a cylindrical piston and an attachment, and the latter generally uses a wire or ribbon to crimp around the rest ossicles. Three types of stapes prostheses are presented in Figure 4. Previous studies have shown that the parameters of the piston stapes prostheses, including the attachment condition, contacting area, and implanted depth, can significantly influence the performance of the prosthesis after implantation (73-75).
The crimping connection represents the contact status between the attachment and the ossicles. Some studies on temporal bones have shown that crimping conditions (without crimping, loose crimping, tight crimping) affect hearing reconstruction (76). Williams et al. designed two different stapes replacement prostheses with different tightness between ossicular chains (77). Joint flexibility was changed by setting different boundary conditions and the number of joint connections. The results showed that the tightness of the prosthesis in the rest ossicular chain was an essential factor for the reconstruction of natural frequency and vibration mode.
The contact area is also a crucial parameter for optimizing stapes prostheses. Böhnke and Arnold designed two cylindrical stapes prostheses with different cylinder cross-sectional areas and implanted them into a spiral cochlear model. They found that the BM displacement peak was increased by enlarging the stapes prosthesis area, as the pure-tone threshold level decreased with a growing prosthesis area (78). Similarly, Kwacz et al. demonstrated that a more extensive area had a better hearing performance based on a box model of the cochlea (79). Consistent results have also been demonstrated in numerous clinical trials (16,17). Some detailed parameters, such as implanted depth that has been found clinically, also need to be optimized for specific stapes prostheses with the FEM (72).
Active MEI
Compared with the passive MEIs mentioned above, active MEIs, such as Vibrant Soundbridge (80), are more successful in the clinic. Active MEIs can be divided into partially and totally implanted middle ear devices. The typical partially implantable active MEI consists of outer and inner parts. The outer part contains microphones, primary induction coils, and batteries, while the inner part comprises secondary induction coils and actuators. The actuator, which is attached to the ossicular chain, is the most critical component of the inner parts. Piezoelectric and electromagnetic transducers are typical actuators for partially implanted middle ear prostheses (81,82).
There are various partially active MEIs with different driver concepts and attachment points. A combination of the FE model of the ear and prosthesis could be used to optimize the MEI designing parameters; for example, the implantation position, direction, and physical characteristics of transducers, including magnets, attachments, and coils. Transducer attachment sites include the umbo, incus body, incus long process, and stapes. Studies have shown that either the stapes head or footplate can produce better hearing performance than other sites (83,84). It has also been shown that a high coupling stiffness between the attachment clip and the ossicular chain is an optimization factor that can help maximize the stimulation efficiency of the transducer (61).
The stimulation angle of the implanted transducer influences hearing performance. For example, the ratio of equivalent sound pressure is reduced when the excitation direction is 20° and 60° off the longitudinal axis of the stapes (84). Mocanu et al. reported the same conclusion when the excitation direction was 45°–60° off the longitudinal stapes axis (85). Therefore, tilting of the actuator from the stapes longitudinal axis is likely to reduce hearing performance. The mass of the transducer also affects the ear response. Gan et al. found that a lower mass loading of 22.5 mg to the incus long process produced an average improvement of 3.5 dB, compared to 37.5 mg from 250 to 8,000 Hz (86). For the eardrum driving transducer, as the mass increases, the displacement of the stapes will decrease more above 2,000 Hz. For the floating mass transducer, as the mass increases, the displacement of the stapes will deteriorate above 750 Hz (87).
The implanted inner parts convert sound signals into vibrations by directly acting on the ossicular chain. Forward stimulation is a method of achieving hearing compensation by constructing a complete auditory pathway. In most cases, the driving site on the cochlea is the OW. In addition, there is also direct stimulation on the RW to transmit vibrational signals, causing changes in the inner ear pressure to restore hearing, known as reverse stimulation (63). An actuator to stimulate the RW membrane becomes feasible when it is difficult to couple the actuator with the ossicles in patients with ossicular chain injury. Similar to the forward stimulation, parameters such as the contact area and mass of the transducer are considered in the RW drivers. Zhang and Gan studied two RW actuators with different masses and areas and reported that the equivalent sound pressure produced by the two types of drivers is different (83). Tian et al. further studied the effect of the transducer area and found that an actuator occupying 25% of the RW area can produce a higher equivalent sound pressure (88).
Nakajima et al. demonstrated that a coupling layer between the transducer and the RW could improve hearing performance (89). Arnold et al. reported a similar conclusion from a specimen experiment (90). Tian et al. showed that the presence of a coupling layer could reduce the influence of the contact area size on equivalent sound pressure compared to a direct coupling on the interface. Overall, a coupling layer with a lower Young’s modulus can perform better, which may benefit the structural design of the actuator (88). Liu et al. further expanded the range of the transducer area and the elastic modulus of the coupling layer, which was consistent with Tian et al.’s work (88,91).
Loading on the RW transducer can influence hearing performance. Lupo et al. conducted animal experiments and showed that changes in the transducer loading pressure do not affect the performance (92). However, Maier et al. confirmed that applying static preload on the transducer could improve the RW stimulation performance in a human cadaver temporal bone experiment (93). Liu et al. demonstrated that static preload on the RW transducer could slightly reduce low-frequency performance but increase high-frequency performance using the FEM (91). Therefore, applying static preload on the transducer is a better treatment for patients with high-frequency hearing loss.
In addition to the partially implanted active middle ear devices, totally implanted active MEIs can also benefit from the FEM. Gan et al. designed a totally implantable hearing system, including an implantable coil, microphone, audio signal processor, rechargeable battery, and transducer, to study the coupling simulation between the transducer and coil using the FEM. They found that active stimulation of the coupling coil could produce a higher stapes displacement response compared to when the stimulus was applied to the ear canal either without a transducer or a coupling coil (94). Gan et al. also studied the mass load effect using the same model, and all of the results were consistent with their temporal experiment. Moreover, this work demonstrated the advantages of designing and optimizing prostheses using the FEM, which is convenient and repeatable when optimizing the various parameters (94). Therefore, the FEM could be used to study relevant factors in totally implantable active middle ear devices, such as the coils as well as the microphone’s mass, position, and material.
Models for the CI
The most widely used inner ear prosthesis is the CI. Coding strategies (18) and speech processors (95) can improve hearing perception. Electrodes directly stimulating the auditory nerves are critical for optimization. The FEM has been used to optimize the shape, positions, stimulation strategies, and other parameters of the electrodes (96). In addition, the FEM can even simulate some situations that are impossible to perform in a real human cochlea. For example, the 3D CI model provides information about cochlear electrophysiology and neurophysiology from a numerical point of view, which is helpful for deep and scale investigations that are not feasible in animals or living humans (97).
The shape of the CI electrodes can be classified as planar, banded, half banded, and ball electrodes, which affect the efficiency of electrical stimulation. Studies have shown that the planar electrode has the highest stimulation efficiency among the other electrodes (98). Some researchers have also studied the position of the electrode (99). Electrode placement includes the modiolar, midscala, and lateral positions, which correspond to electrodes on the market, such as pre-curved modiolar hugging, midscala, and straight lateral wall electrode arrays. Frijns et al. compared lateral and modiolar hugging electrode positions using a volume conduction model of the cochlea. They found that the latter position could reduce the current thresholds while retaining excellent spatial selectivity in the basal turn, which might be because the electrode was closer to the nerve fiber and lowered the impedance (48). The clinical study is consistent with the result of the simulation. The modiolar electrode had better hearing preservation than midscala or lateral electrode (100). However, some results have shown that the electrode-modiolus distance does not affect the stimulation threshold (101). Overall, the relationship between electrode to modiolus distance and the current levels is still unclear (102-105). This uncertainty could be due to the potentially varying survival nerve fibers in different CI patients. For people with few nerve fibers survival, the distance between electrodes may not have a significant impact. The FEM could be used to establish nerve fiber models of patients with different types of hearing impairment for further investigation.
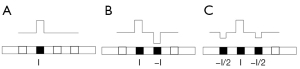
The electrode stimulation strategy, which determines electric field distributions inside the cochlea (106), is a vital factor that has been modified during the CI development stage. Monopolar stimulation can cause extensive electrical interactions, and thus, research into multielectrode stimulation strategies, such as bipolar or tripolar stimulation, has been conducted (106-108). Bipolar stimulation refers to the stimulation of two adjacent electrodes with opposite polarities. Three adjacent electrodes are stimulated in tripolar stimulation, where the center electrode and both sides receive stimulation with opposite polarity. The stimulation current amplitude is half that of the center electrode, as shown in Figure 5. The FEM calculates the spatial selectivity by measuring neural responses under different stimulation strategies. Clinical evaluation can be carried out through postoperative evaluation. Model and clinical experiments have shown that tripolar and bipolar stimulations cover narrower auditory nerve regions than the traditional monopolar stimulation, which signifies better spatial selectivity (19,106,109-111). Although multielectrode stimulation strategies have been widely studied to increase spatial selectivity, monopolar stimulation is still the most common configuration. Because the bipolar and tripolar stimulations need a higher current, thereby reducing or eliminating the current focusing (111-113). In short, multielectrode stimulation requires further research combined with battery development. Furthermore, current steering controls the generation of virtual channels by reasonably distributing the current to the two adjacent electrodes, which is also a promising research direction (114,115).
Although the most widely used CI is partially implanted, the totally implantable cochlear implant (TICI), invisible from the outside, is more promising (116,117). All of the parameters of the implantable parts, such as the electrodeposition and configuration, can be analyzed using FEM, which is similar to the partially implantable CI. Furthermore, microphones, primary induction coils, and batteries that may affect signal transmission should be considered. For example, the surrounding tissues may affect the coil’s working status (118). In addition, electrical coupling between the coil and speech processor that may influence the transmission efficiency also requires further investigation.
Discussion
This paper discussed the design and optimization of auditory prostheses using the FEM. The FEM uses mathematical approximations to simulate the ear and hearing device with parametrical geometry and materials. Imaging and measuring technologies provide geometrical data for modeling, which allows for the determination of the model’s accuracy and simulation credibility. A designed prosthesis model can be implanted into the ear model to simulate some clinically relevant situations. The post-implantation response using FE models could be used as an indicator to evaluate the performance of the prosthesis. Some cadaveric or animal experiments have identified valuable parameters, such as the mass or position of the middle ear prosthesis or the position of the CI electrode, which should be optimized to improve hearing performance. The FEM can overcome the limitations of testing parameters from multiple tests in cadaveric or animal experiments, reduce costs, and increase repeatability. However, this does not mean that the FEM can completely replace cadaveric or animal experiments. The convenience of FEM should be utilized to explore more effective directions for animal experiments. Finally, we proposed some suggestions about auditory prosthesis design and optimization with the FEM.
The scope of the auditory model
Currently, most FEM-based auditory models are used for designing prostheses that act on the auditory peripheral system. However, many auditory prostheses act on the auditory central nervous system, such as ABIs and AMIs (9,10). There is a lack of research about ABI and AMI design or optimization using the FEM, which may be because the model complexity is relatively high. In the future, a hybrid model could be built, which includes the ear and other structures of the auditory center from the cochlea to the auditory cortex (such as nerve fibers) and integrates implanted parts (such as electrodes), to study the post-implanted performance of auditory prostheses by observing the potential distribution. As for ABIs or AMIs, the post-implantation response can be used to design and optimize parameters such as electrodeposition or stimulation strategy.
Accuracy of ear and prosthesis model
It is also essential to determine whether the ear and prosthesis models effectively reflect a clinically relevant situation. Firstly, the level of detail included in a model should be determined based on the research objective; a more detailed model does not necessarily mean higher accuracy. Secondly, the material properties of the ear or prosthesis model require more accurate measurement data, such as the non-linear mechanical properties of soft tissues (119-124). Thirdly, many auditory prostheses are designed based on normal-hearing specimens and cannot reflect the features of lesions. For example, the RW stimulation prosthesis is designed for patients with a damaged ossicular chain. Different deformations of the ossicular chain model can affect the observed ear response, further influencing the design and optimization of the prosthesis (29). Therefore, a model that can reflect the lesion is important.
Modeling time and complexity
Building an accurate and detailed ear and prosthesis model is time-consuming and complicated. Modeling work requires background knowledge from various fields, including anatomy, physiology, audiology, and mechanical engineering. A complicated, highly detailed ear and prosthesis model may be required for studying neural responses or a personalized design, leading to a longer modeling time. Moreover, the simulation time varies with the complexity of the model, ranging from minutes to hours or days, and depends on the computer’s configuration (125).
The FEM can be utilized to shorten the decision time and reduce operational complexity for surgical planning. Therefore, a simple, convenient, and rapid modeling platform is necessary. The platform should automatically and promptly establish a patient-specific ear model and quickly suggest a well-matched prosthesis type and surgical plan. Moreover, the platform should also predict the recovery of hearing performance after implantation.
Evaluation
Numerous studies have shown that auditory-related responses calculated using numerical models can effectively reflect the optimization performance. For example, FE models can predict the evoked compound action potential and compare it with clinical measurements to estimate whether the given CI stimulation level is suitable (126). However, many calculated responses obtained from the model are difficult to relate to clinical data directly. Therefore, researchers need to identify more indicators and compare them with experimental or clinical measurements to evaluate hearing performance.
Acknowledgments
Funding: This work was supported by grants from the National Natural Science Foundation of China (No. 81971698 to GN) and the Beijing-Tianjin-Hebei Basic Research Cooperation Project (No. 18JCZDJC45300 to GN).
Footnote
Reporting Checklist: The authors have completed the Narrative Review reporting checklist. Available at https://atm.amegroups.com/article/view/10.21037/atm-22-2792/rc
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://atm.amegroups.com/article/view/10.21037/atm-22-2792/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Pickles JO. Auditory pathways: anatomy and physiology. Handb Clin Neurol 2015;129:3-25. [Crossref] [PubMed]
- Nieman CL, Oh ES. Hearing Loss. Ann Intern Med 2020;173:ITC81-96. [Crossref] [PubMed]
- Simon E, Perrot X, Mertens P. Functional anatomy of the cochlear nerve and the central auditory system. Neurochirurgie 2009;55:120-6. [Crossref] [PubMed]
- Hill-Feltham PR, Johansson ML, Hodgetts WE, et al. Hearing outcome measures for conductive and mixed hearing loss treatment in adults: a scoping review. Int J Audiol 2021;60:239-45. [Crossref] [PubMed]
- Banakis Hartl RM, Jenkins HA. Implantable Hearing Aids: Where are we in 2020? Laryngoscope Investig Otolaryngol 2020;5:1184-91. [Crossref] [PubMed]
- Korver AM, Smith RJ, Van Camp G, et al. Congenital hearing loss. Nat Rev Dis Primers 2017;3:16094. [Crossref] [PubMed]
- Luers JC, Hüttenbrink KB. Surgical anatomy and pathology of the middle ear. J Anat 2016;228:338-53. [Crossref] [PubMed]
- Wilson BS, Dorman MF. Cochlear implants: current designs and future possibilities. J Rehabil Res Dev 2008;45:695-730. [Crossref] [PubMed]
- Deep NL, Roland JT Jr. Auditory Brainstem Implantation: Candidacy Evaluation, Operative Technique, and Outcomes. Otolaryngol Clin North Am 2020;53:103-13. [Crossref] [PubMed]
- Lim HH, Lenarz T. Auditory midbrain implant: research and development towards a second clinical trial. Hear Res 2015;322:212-23. [Crossref] [PubMed]
- Kaplan AB, Kozin ED, Puram SV, et al. Auditory brainstem implant candidacy in the United States in children 0-17 years old. Int J Pediatr Otorhinolaryngol 2015;79:310-5. [Crossref] [PubMed]
- Arechvo I, Bornitz M, Lasurashvili N, et al. New total ossicular replacement prostheses with a resilient joint: experimental data from human temporal bones. Otol Neurotol 2012;33:60-6. [Crossref] [PubMed]
- Balkany TJ, Connell SS, Hodges AV, et al. Conservation of residual acoustic hearing after cochlear implantation. Otol Neurotol 2006;27:1083-8. [Crossref] [PubMed]
- Boggess WJ, Baker JE, Balkany TJ. Loss of residual hearing after cochlear implantation. Laryngoscope 1989;99:1002-5. [Crossref] [PubMed]
- Zahnert T, Schmidt R, Huttenbrink KB. FE-simulation of vibrations of the Dresden middle ear prosthesis. In: Huttenbrink KB, editor. Middle ear mechanics in research and otosurgery. Dresden: UniMedia GmbH. 1997:200-6.
- Shabana YK, Ghonim MR, Pedersen CB. Stapedotomy: does prosthesis diameter affect outcome? Clin Otolaryngol Allied Sci 1999;24:91-4. [Crossref] [PubMed]
- Marchese MR, Cianfrone F, Passali GC, et al. Hearing results after stapedotomy: role of the prosthesis diameter. Audiol Neurootol 2007;12:221-5. [Crossref] [PubMed]
- Adams D, Ajimsha KM, Barberá MT, et al. Multicentre evaluation of music perception in adult users of Advanced Bionics cochlear implants. Cochlear Implants Int 2014;15:20-6. [Crossref] [PubMed]
- Nogueira W, Würfel W, Penninger RT, et al. Development of a Model of the Electrically Stimulated Cochlea. In: Lenarz T, Wriggers P. editors. Biomedical Technology. Lecture Notes in Applied and Computational Mechanics. Cham.: Springer, 2014;74:145-61.
- O'Connell BP, Hunter JB, Haynes DS, et al. Insertion depth impacts speech perception and hearing preservation for lateral wall electrodes. Laryngoscope 2017;127:2352-7. [Crossref] [PubMed]
- Jakob TF, Kromeier J, Baumann T, et al. Experimental Simulation of Clinical Borderline Situations in Temporal Bone Specimens After Ossiculoplasty. Ear Hear 2018;39:131-8. [Crossref] [PubMed]
- Rönnblom A, Gladiné K, Niklasson A, et al. A New, Promising Experimental Ossicular Prosthesis: A Human Temporal Bone Study With Laser Doppler Vibrometry. Otol Neurotol 2020;41:537-44. [Crossref] [PubMed]
- Ulku CH, Cheng JT, Guignard J, et al. Comparisons of the mechanics of partial and total ossicular replacement prostheses with cartilage in a cadaveric temporal bone preparation. Acta Otolaryngol 2014;134:776-84. [Crossref] [PubMed]
- Mudry A, Mills M. The early history of the cochlear implant: a retrospective. JAMA Otolaryngol Head Neck Surg 2013;139:446-53. [Crossref] [PubMed]
- Merzenich MM, Michelson RP, Pettit CR, et al. Neural encoding of sound sensation evoked by electrical stimulation of the acoustic nerve. Ann Otol Rhinol Laryngol 1973;82:486-503. [Crossref] [PubMed]
- Wilson BS, Finley CC, Lawson DT, et al. Design and evaluation of a continuous interleaved sampling (CIS) processing strategy for multichannel cochlear implants. J Rehabil Res Dev 1993;30:110-6. [PubMed]
- Park IY, Shimizu Y, O'Connor KN, et al. Comparisons of electromagnetic and piezoelectric floating-mass transducers in human cadaveric temporal bones. Hear Res 2011;272:187-92. [Crossref] [PubMed]
- Gan RZ, Reeves BP, Wang X. Modeling of sound transmission from ear canal to cochlea. Ann Biomed Eng 2007;35:2180-95. [Crossref] [PubMed]
- Liu H, Zhang H, Yang J, et al. Influence of ossicular chain malformation on the performance of round-window stimulation: A finite element approach. Proc Inst Mech Eng H 2019;233:584-94. [Crossref] [PubMed]
- Zhao F, Koike T, Wang J, et al. Finite element analysis of the middle ear transfer functions and related pathologies. Med Eng Phys 2009;31:907-16. [Crossref] [PubMed]
- Frijns JH, de Snoo SL, Schoonhoven R. Potential distributions and neural excitation patterns in a rotationally symmetric model of the electrically stimulated cochlea. Hear Res 1995;87:170-86. [Crossref] [PubMed]
- Kwacz M, Marek P, Borkowski P, et al. Effect of different stapes prostheses on the passive vibration of the basilar membrane. Hear Res 2014;310:13-26. [Crossref] [PubMed]
- Prendergast PJ, Ferris P, Rice HJ, et al. Vibro-acoustic modelling of the outer and middle ear using the finite-element method. Audiol Neurootol 1999;4:185-91. [Crossref] [PubMed]
- Ferris P, Prendergast PJ. Middle-ear dynamics before and after ossicular replacement. J Biomech 2000;33:581-90. [Crossref] [PubMed]
- Williams KR, Blayney AW, Rice HJ. Development of a finite element model of the middle ear. Rev Laryngol Otol Rhinol (Bord) 1996;117:259-64. [PubMed]
- Wada H, Metoki T, Kobayashi T. Analysis of dynamic behavior of human middle ear using a finite-element method. J Acoust Soc Am 1992;92:3157-68. [Crossref] [PubMed]
- Funnell WR, Laszlo CA. Modeling of the cat eardrum as a thin shell using the finite-element method. J Acoust Soc Am 1978;63:1461-7. [Crossref] [PubMed]
- Halm S, Haberthür D, Eppler E, et al. Micro-CT imaging of Thiel-embalmed and iodine-stained human temporal bone for 3D modeling. J Otolaryngol Head Neck Surg 2021;50:33. [Crossref] [PubMed]
- Beer HJ, Bornitz M, Hardtke HJ, et al. Modelling of components of the human middle ear and simulation of their dynamic behaviour. Audiol Neurootol 1999;4:156-62. [Crossref] [PubMed]
- Gan RZ, Feng B, Sun Q. Three-dimensional finite element modeling of human ear for sound transmission. Ann Biomed Eng 2004;32:847-59. [Crossref] [PubMed]
- Poznyakovskiy AA, Zahnert T, Kalaidzidis Y, et al. The creation of geometric three-dimensional models of the inner ear based on micro computer tomography data. Hear Res 2008;243:95-104. [Crossref] [PubMed]
- Uzun H, Curthoys IS, Jones AS. A new approach to visualizing the membranous structures of the inner ear - high resolution X-ray micro-tomography. Acta Otolaryngol 2007;127:568-73. [Crossref] [PubMed]
- Lee CF, Chen PR, Lee WJ, et al. Three-dimensional reconstruction and modeling of middle ear biomechanics by high-resolution computed tomography and finite element analysis. Laryngoscope 2006;116:711-6. [Crossref] [PubMed]
- Decraemer WF, Dirckx JJ, Funnell WR. Three-dimensional modelling of the middle-ear ossicular chain using a commercial high-resolution X-ray CT scanner. J Assoc Res Otolaryngol 2003;4:250-63. [Crossref] [PubMed]
- Ni G, Sun L, Elliott SJ. A linearly tapered box model of the cochlea. J Acoust Soc Am 2017;141:1793. [Crossref] [PubMed]
- Ren LJ, Yu Y, Fang YQ, et al. Finite element simulation of cochlear traveling wave under air and bone conduction hearing. Biomech Model Mechanobiol 2021;20:1251-65. [Crossref] [PubMed]
- Briaire JJ, Frijns JH. Field patterns in a 3D tapered spiral model of the electrically stimulated cochlea. Hear Res 2000;148:18-30. [Crossref] [PubMed]
- Frijns JH, Briaire JJ, Grote JJ. The importance of human cochlear anatomy for the results of modiolus-hugging multichannel cochlear implants. Otol Neurotol 2001;22:340-9. [Crossref] [PubMed]
- Nogueira W, Schurzig D, Büchner A, et al. Validation of a Cochlear Implant Patient-Specific Model of the Voltage Distribution in a Clinical Setting. Front Bioeng Biotechnol 2016;4:84. [Crossref] [PubMed]
- Saba R, Elliott SJ, Wang S. Modelling the effects of cochlear implant current focusing. Cochlear Implants Int 2014;15:318-26. [Crossref] [PubMed]
- Micco AG, Richter CP. Electrical resistivity measurements in the mammalian cochlea after neural degeneration. Laryngoscope 2006;116:1334-41. [Crossref] [PubMed]
- Poznyakovskiy AA, Zahnert T, Kalaidzidis Y, et al. A segmentation method to obtain a complete geometry model of the hearing organ. Hear Res 2011;282:25-34. [Crossref] [PubMed]
- Braun K, Böhnke F, Stark T. Three-dimensional representation of the human cochlea using micro-computed tomography data: presenting an anatomical model for further numerical calculations. Acta Otolaryngol 2012;132:603-13. [Crossref] [PubMed]
- Lareida A, Beckmann F, Schrott-Fischer A, et al. High-resolution X-ray tomography of the human inner ear: synchrotron radiation-based study of nerve fibre bundles, membranes and ganglion cells. J Microsc 2009;234:95-102. [Crossref] [PubMed]
- Ni G, Elliott SJ, Baumgart J. Finite-element model of the active organ of Corti. J R Soc Interface 2016;13:20150913. [Crossref] [PubMed]
- Sakellarios AI, Tachos NS, Rigas G, et al. A validated methodology for the 3D reconstruction of cochlea geometries using human microCT images. Measurement Science and Technology 2017;28:54001. [Crossref]
- Frijns JH, Mooij J, ten Kate JH. A quantitative approach to modeling mammalian myelinated nerve fibers for electrical prosthesis design. IEEE Trans Biomed Eng 1994;41:556-66. [Crossref] [PubMed]
- Frijns JH, ten Kate JH. A model of myelinated nerve fibres for electrical prosthesis design. Med Biol Eng Comput 1994;32:391-8. [Crossref] [PubMed]
- Ma J, Yao W, Hu B. Simulation of the Multiphysical Coupling Behavior of Active Hearing Mechanism Within Spiral Cochlea. J Biomech Eng 2020;142:091005. [Crossref] [PubMed]
- Homma K, Du Y, Shimizu Y, et al. Ossicular resonance modes of the human middle ear for bone and air conduction. J Acoust Soc Am 2009;125:968-79. [Crossref] [PubMed]
- Wang X, Hu Y, Wang Z, et al. Finite element analysis of the coupling between ossicular chain and mass loading for evaluation of implantable hearing device. Hear Res 2011;280:48-57. [Crossref] [PubMed]
- Homma K, Shimizu Y, Kim N, et al. Effects of ear-canal pressurization on middle-ear bone- and air-conduction responses. Hear Res 2010;263:204-15. [Crossref] [PubMed]
- Zhang J, Zou D, Tian J, et al. A comparative finite-element analysis of acoustic transmission in human cochlea during forward and reverse stimulations. Applied Acoustics 2019;145:278-89. [Crossref]
- Zhang J, Tian J, Ta N, et al. Finite element analysis of round-window stimulation of the cochlea in patients with stapedial otosclerosis. J Acoust Soc Am 2019;146:4122. [Crossref] [PubMed]
- Brown MA, Ji XD, Gan RZ. 3D Finite Element Modeling of Blast Wave Transmission from the External Ear to Cochlea. Ann Biomed Eng 2021;49:757-68. [Crossref] [PubMed]
- Bittencourt AG, Burke PR, Jardim Ide S, et al. Implantable and semi-implantable hearing AIDS: a review of history, indications, and surgery. Int Arch Otorhinolaryngol 2014;18:303-10. [Crossref] [PubMed]
- Connor SEJ. Contemporary imaging of auditory implants. Clin Radiol 2018;73:19-34. [Crossref] [PubMed]
- Kelly DJ, Prendergast PJ, Blayney AW. The effect of prosthesis design on vibration of the reconstructed ossicular chain: a comparative finite element analysis of four prostheses. Otol Neurotol 2003;24:11-9. [Crossref] [PubMed]
- Koike T, Wada H, Kobayashi T. Analysis of the finite-element method of transfer function of reconstructed middle ears and their postoperative changes. In: Rosowski JJ, Merchant SN. editors. The function and mechanics of normal, diseased and reconstructed middle ears. The Hague: Kugler Publications, 2000:309-20.
- Yao W, Li B, Huang X, et al. Restoring hearing using total ossicular replacement prostheses--analysis of 3D finite element model. Acta Otolaryngol 2012;132:152-9. [Crossref] [PubMed]
- Kwacz M, Sołyga M, Mrówka M, et al. New chamber stapes prosthesis - A preliminary assessment of the functioning of the prototype. PLoS One 2017;12:e0178133. [Crossref] [PubMed]
- Kiryk EA, Kamieniecki K, Kwacz M. Design of a resilient ring for middle ear's chamber stapes prosthesis. Comput Methods Biomech Biomed Engin 2018;21:771-9. [Crossref] [PubMed]
- Gil Mun S, Scheffner E, Müller S, et al. Stapes piston insertion depth and clinical correlations. Acta Otolaryngol 2019;139:829-32. [Crossref] [PubMed]
- Laske RD, Röösli C, Chatzimichalis MV, et al. The influence of prosthesis diameter in stapes surgery: a meta-analysis and systematic review of the literature. Otol Neurotol 2011;32:520-8. [Crossref] [PubMed]
- Teig E, Lindeman HH. Stapedotomy Piston Diameter – Is Bigger Better? Oto-rhino-laryngologia nova 1999;9:252-6.
- Huber AM, Ma F, Felix H, et al. Stapes prosthesis attachment: the effect of crimping on sound transfer in otosclerosis surgery. Laryngoscope 2003;113:853-8. [Crossref] [PubMed]
- Williams KR, Blayney AW, Lesser TH A. 3-D finite element analysis of the natural frequencies of vibration of a stapes prosthesis replacement reconstruction of the middle ear. Clin Otolaryngol Allied Sci 1995;20:36-44. [Crossref] [PubMed]
- Böhnke F, Arnold W. Finite element model of the stapes-inner ear interface. Adv Otorhinolaryngol 2007;65:150-4. [PubMed]
- Kwacz M, Marek P, Borkowski P, et al. A three-dimensional finite element model of round window membrane vibration before and after stapedotomy surgery. Biomech Model Mechanobiol 2013;12:1243-61. [Crossref] [PubMed]
- Zenner HP, Leysieffer H. Total implantation of the Implex TICA hearing amplifier implant for high frequency sensorineural hearing loss: the Tübingen University experience. Otolaryngol Clin North Am 2001;34:417-46. [Crossref] [PubMed]
- Snik AF, Cremers CW. First audiometric results with the Vibrant soundbridge, a semi-implantable hearing device for sensorineural hearing loss. Audiology 1999;38:335-8. [Crossref] [PubMed]
- Goode RL, Rosenbaum ML, Maniglia AJ. The history and development of the implantable hearing aid. Otolaryngol Clin North Am 1995;28:1-16. [Crossref] [PubMed]
- Zhang X, Gan RZ. A comprehensive model of human ear for analysis of implantable hearing devices. IEEE Trans Biomed Eng 2011;58:3024-7. [Crossref] [PubMed]
- Bornitz M, Hardtke HJ, Zahnert T. Evaluation of implantable actuators by means of a middle ear simulation model. Hear Res 2010;263:145-51. [Crossref] [PubMed]
- Mocanu H, Bornitz M, Lasurashvili N, et al. Evaluation of Vibrant® Soundbridge™ positioning and results with laser doppler vibrometry and the finite element model. Exp Ther Med 2021;21:262. [Crossref] [PubMed]
- Gan RZ, Sun Q, Dyer RK Jr, et al. Three-dimensional modeling of middle ear biomechanics and its applications. Otol Neurotol 2002;23:271-80. [Crossref] [PubMed]
- Liu H, Ge S, Cheng G, et al. The effect of implantable transducers on middle ear transfer function: a comparative numerical analysis. Journal of Mechanics in Medicine and Biology 2015;16:1-16.
- Tian J, Huang X, Rao Z, et al. Finite element analysis of the effect of actuator coupling conditions on round window stimulation. J Mech Med Biol 2015;15:1550048. [Crossref]
- Nakajima HH, Dong W, Olson ES, et al. Evaluation of round window stimulation using the floating mass transducer by intracochlear sound pressure measurements in human temporal bones. Otol Neurotol 2010;31:506-11. [Crossref] [PubMed]
- Arnold A, Stieger C, Candreia C, et al. Factors improving the vibration transfer of the floating mass transducer at the round window. Otol Neurotol 2010;31:122-8. [Crossref] [PubMed]
- Liu H, Xu D, Yang J, et al. Analysis of the influence of the transducer and its coupling layer on round window stimulation. Acta Bioeng Biomech 2017;19:103-11. [PubMed]
- Lupo JE, Koka K, Hyde BJ, et al. Physiological assessment of active middle ear implant coupling to the round window in Chinchilla lanigera. Otolaryngol Head Neck Surg 2011;145:641-7. [Crossref] [PubMed]
- Maier H, Salcher R, Schwab B, et al. The effect of static force on round window stimulation with the direct acoustic cochlea stimulator. Hear Res 2013;301:115-24. [Crossref] [PubMed]
- Gan RZ, Dai C, Wang X, et al. A totally implantable hearing system--design and function characterization in 3D computational model and temporal bones. Hear Res 2010;263:138-44. [Crossref] [PubMed]
- Dazert S, Thomas JP, Büchner A, et al. Off the ear with no loss in speech understanding: comparing the RONDO and the OPUS 2 cochlear implant audio processors. Eur Arch Otorhinolaryngol 2017;274:1391-5. [Crossref] [PubMed]
- Hanekom T. Three-dimensional spiraling finite element model of the electrically stimulated cochlea. Ear Hear 2001;22:300-15. [Crossref] [PubMed]
- Hanekom T, Hanekom JJ. Three-dimensional models of cochlear implants: A review of their development and how they could support management and maintenance of cochlear implant performance. Network 2016;27:67-106. [Crossref] [PubMed]
- Lai WD, Choi CTM. Incorporating the Electrode-Tissue Interface to Cochlear Implant Models. IEEE Transactions on Magnetics 2007;43:1721-4. [Crossref]
- Areias B, Parente MPL, Gentil F, et al. Finite element modelling of the surgical procedure for placement of a straight electrode array: Mechanical and clinical consequences. J Biomech 2021;129:110812. [Crossref] [PubMed]
- Ramos-de-Miguel A, Falcón-González JC, Ramos-Macias A. Analysis of Neural Interface When Using Modiolar Electrode Stimulation. Radiological Evaluation, Trans-Impedance Matrix Analysis and Effect on Listening Effort in Cochlear Implantation. J Clin Med 2021;10:3962. [Crossref] [PubMed]
- Hughes ML, Abbas PJ. Electrophysiologic channel interaction, electrode pitch ranking, and behavioral threshold in straight versus perimodiolar cochlear implant electrode arrays. J Acoust Soc Am 2006;119:1538-47. [Crossref] [PubMed]
- Kalkman RK, Briaire JJ, Dekker DM, et al. Place pitch versus electrode location in a realistic computational model of the implanted human cochlea. Hear Res 2014;315:10-24. [Crossref] [PubMed]
- Davis TJ, Zhang D, Gifford RH, et al. Relationship Between Electrode-to-Modiolus Distance and Current Levels for Adults With Cochlear Implants. Otol Neurotol 2016;37:31-7. [Crossref] [PubMed]
- van der Beek FB, Briaire JJ, van der Marel KS, et al. Intracochlear Position of Cochlear Implants Determined Using CT Scanning versus Fitting Levels: Higher Threshold Levels at Basal Turn. Audiol Neurootol 2016;21:54-67. [Crossref] [PubMed]
- Saunders E, Cohen L, Aschendorff A, et al. Threshold, comfortable level and impedance changes as a function of electrode-modiolar distance. Ear Hear 2002;23:28S-40S. [Crossref] [PubMed]
- Zhu Z, Tang Q, Zeng FG, et al. Cochlear-implant spatial selectivity with monopolar, bipolar and tripolar stimulation. Hear Res 2012;283:45-58. [Crossref] [PubMed]
- Seyyedi M, Eddington DK, Nadol JB Jr. Effect of monopolar and bipolar electric stimulation on survival and size of human spiral ganglion cells as studied by postmortem histopathology. Hear Res 2013;302:9-16. [Crossref] [PubMed]
- Chari DA, Jiradejvong P, Limb CJ. Tripolar Stimulation Improves Polyphonic Pitch Detection in Cochlear Implant Users. Otol Neurotol 2019;40:38-46. [Crossref] [PubMed]
- Tognola G, Pesatori A, Norgia M, et al. Numerical Modeling and Experimental Measurements of the Electric Potential Generated by Cochlear Implants in Physiological Tissues. IEEE Transactions on Instrumentation and Measurement 2007;56:187-93. [Crossref]
- Bonham BH, Litvak LM. Current focusing and steering: modeling, physiology, and psychophysics. Hear Res 2008;242:141-53. [Crossref] [PubMed]
- Landsberger DM, Padilla M, Srinivasan AG. Reducing current spread using current focusing in cochlear implant users. Hear Res 2012;284:16-24. [Crossref] [PubMed]
- Chatterjee M, Shannon RV. Forward masked excitation patterns in multielectrode electrical stimulation. J Acoust Soc Am 1998;103:2565-72. [Crossref] [PubMed]
- Kwon BJ, van den Honert C. Effect of electrode configuration on psychophysical forward masking in cochlear implant listeners. J Acoust Soc Am 2006;119:2994-3002. [Crossref] [PubMed]
- Choi CT, Hsu CH. Conditions for generating virtual channels in cochlear prosthesis systems. Ann Biomed Eng 2009;37:614-24. [Crossref] [PubMed]
- Koch DB, Downing M, Osberger MJ, et al. Using current steering to increase spectral resolution in CII and HiRes 90K users. Ear Hear 2007;28:38S-41S. [Crossref] [PubMed]
- Cohen N. The totally implantable cochlear implant. Ear Hear 2007;28:100S-1S. [Crossref] [PubMed]
- Xu XD, Chi FL. A review about the research progress of the acoustical-electrical transducer for totally implantable cochlear implant. Zhonghua Er Bi Yan Hou Tou Jing Wai Ke Za Zhi 2017;52:127-30. [PubMed]
- Ozturan O, Yenigun A, Senturk E, et al. Temporal Scalp Thickness, Body Mass Index, and Suprafascial Placement of Receiver Coil of the Cochlear Implant. J Craniofac Surg 2017;28:e781-5. [Crossref] [PubMed]
- Ladak HM, Funnell WR. Finite-element modeling of the normal and surgically repaired cat middle ear. J Acoust Soc Am 1996;100:933-44. [Crossref] [PubMed]
- Bai S, Encke J, Obando-Leitón M, et al. Electrical Stimulation in the Human Cochlea: A Computational Study Based on High-Resolution Micro-CT Scans. Front Neurosci 2019;13:1312. [Crossref] [PubMed]
- Luo H, Wang F, Cheng C, et al. Mapping the Young's modulus distribution of the human tympanic membrane by microindentation. Hear Res 2019;378:75-91. [Crossref] [PubMed]
- Wong P, George S, Tran P, et al. Development and Validation of a High-Fidelity Finite-Element Model of Monopolar Stimulation in the Implanted Guinea Pig Cochlea. IEEE Trans Biomed Eng 2016;63:188-98. [Crossref] [PubMed]
- Zhang J, Tian J, Ta N, et al. Numerical evaluation of implantable hearing devices using a finite element model of human ear considering viscoelastic properties. Proc Inst Mech Eng H 2016;230:784-94. [Crossref] [PubMed]
- Rohani SA, Ghomashchi S, Agrawal SK, et al. Estimation of the Young's modulus of the human pars tensa using in-situ pressurization and inverse finite-element analysis. Hear Res 2017;345:69-78. [Crossref] [PubMed]
- Motallebzadeh H, Soons JAM, Puria S. Cochlear amplification and tuning depend on the cellular arrangement within the organ of Corti. Proc Natl Acad Sci U S A 2018;115:5762-7. [Crossref] [PubMed]
- Choi CTM, Wang S. Modeling ECAP in Cochlear Implants Using the FEM and Equivalent Circuits. IEEE Transactions on Magnetics 2014;50:49-52. [Crossref]
(English Language Editor: A. Kassem)



