
A finite element analysis of the supportive effect of a new type of rotary support plate on lateral tibial plateau fractures
Introduction
Tibial plateau fracture (TPF) is a common intra-articular fracture resulting from high-energy injury and accounts for 1% of all fractures (1,2). This type of fracture is often caused by the joint surface splitting and collapsing under the simultaneous action of high intensity axial load of the tibia and coronal plane (valgus/varus) stress (3). Due to the special geometric structure and biomechanical characteristics of the human knee joint, about 60% of TPF occur in the lateral column (4). On the basis of imaging anatomy, Ren et al. designed a new type of rotary support bone plate (ARSP; Patent No. CN201520195596.5) and proposed a new surgical approach (5-7) by using the anterolateral skin incision and through the fibula and tibia fibula muscle space. This approach is simple, safe, and effective, and creates little trauma to the surrounding soft tissues of the lateral tibial plateau (5). The new type of support plate used in this approach (Figure 1) which we use the plate to treat TPFs and to reduce and fix the fracture through an anterolateral approach has been proven to be effective in clinical practice (6,7). However, Posterolateral TPFs are often combined with lateral TPFs (8,9). To further improve the biomechanics analysis of the new plate and evaluate the supportive effect of the new plate on lateral TPFs, three-dimensional finite element digital modeling and analysis technology (FEA) was used.
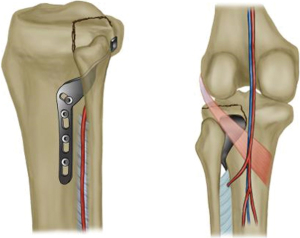
We speculate that the new steel plate plays a supporting role in the lateral fracture of the tibia platform. We investigated the support effect of the new steel plate on lateral TPFs combined with posterior TPFs. We present the following article in accordance with the MDAR reporting checklist (available at https://atm.amegroups.com/article/view/10.21037/atm-22-4529/rc).
Methods
Materials
Two synthetic tibia were used to construct a basic TPF model (left, type 3401; Sawbones, Vashon, WA). All materials were obtained from the same batch to ensure the same product performance, consistency, and geometry, improved control of sample variability, and to avoid congenital malformations, tibial fractures, osteoporosis, and other bone metabolic diseases.
Study methods
Establishment of a model of TPF
The computed tomography (CT) transverse plane of the articular surface of the tibial plateau has previously been defined as the standard measuring plane (10). Based on this definition, we drew a rectangle with the lateral tibial plateau sides. Point A was located at the posterior third of the lateral side and point B was located at the lateral third of the posterior side. The intersection between the line through point A and parallel to the back side of the rectangle and the line through point B and parallel to the medial side of the rectangle was called point C. The angle of 120° with the straight line AC was then generated. The sagittal angle of the fracture line was approximately 80°. The distance between the distal end of the fracture block and the platform was 30 mm (Figure 2A-2C). A fracture line was determined according to a previous study by Chen et al., in which the average fracture line angle of the anterolateral Schatzker type-II TPF was shown to be 149.59°±9.33° (9). Since this ARSP (a new type of rotary support plate) study basically focused on the supportive effect of the lateral bone mass while the collapse was ignored, an angle of 149.59° was chosen between the line of MN and PF. According to Chen et al. (9), the P-spot is the midpoint of the posterior cruciate ligament stop point, the F-spot is the medial tibial nodule 1/3 point, and the PF connection is the neutral axis. MN is a complex tibia plateau fracture (CF) with a lateral fracture block at two points at the edge of the plateau Because this experiment studies the support effect of the new steel plate on the lateral bone mass, the collapse is not considered, and in the collapse case of the finite element software (the posterior lateral bone mass in the Schatzker II platform is mostly collapsed), the angle measurement changes greatly due to the difference in the depth of collapse, so the angle of the simple lateral bone mass in the Schatzker II platform is taken, that is, the angle between mn and PF connection is 150°. Chen et al. also noted that the injury mechanism of each subtype of Schatzker type Ⅱ TPF is similar (9). A band saw was used to cut the bone from the articular surface to the anterolateral side of the synthetic model, generating a fracture line angle of 150° (Figure 2D). The model was established by an experienced surgeon. The model of the fracture line was very similar to that described by Kfuri et al. (8). This model has been shown to be effective and accurate, and can be further tested (9,10).
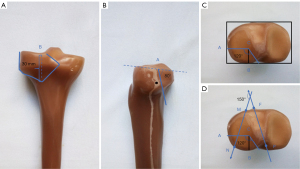
Establishment of an experimental model
The new type of plate and all screws with appropriate sizes (Shandong Weigao Group Medical Polymer Co., Ltd.; Weihai, China) were selected by an experienced surgeon Dong Ren. A 64-slice spiral CT (Previously defined) scanner (Siemens, Erlangen, Germany) was used to scan the model at a tube voltage of 120 kV, current of 200 mA, slice thickness of 1 mm, and interlayer spacing of 1mm. The images were exported in the format of Digital Imaging and Communications in Medicine (DICOM) and imported into the interactive medical imaging control system Mimics 14.0 (Materialise, Leuven, Belgium) to create a 3-dimensional (3D) fracture model.
Finite element analysis
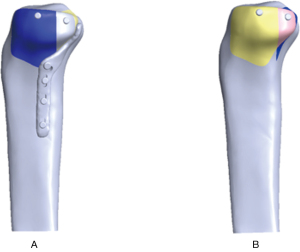
The models of TPF were imported into Geomagic Studio 12.0 (Geomagic, North Carolina) to generate elaborate 3D images. We used handling methods which included tailoring, expanding, and Boolean subtraction. These 3D images were then divided into plane mesh models. The images endowed with material properties, including elastic modulus and Poisson ratio, by reimporting into the Mimics program. The elastic modulus of the cortical bone was 1.68e10 Pascals (Pa) and the Poisson’s ratio was 0.3. The elastic modulus of the cancellous bone was 8.4e8 Pa and the Poisson’s ratio was 0.2; and the elastic modulus of the titanium alloy was 1.05e11 Pa and the Poisson’s ratio was 0.35. The friction force between fracture blocks was set as normal value (11). The model of TPF was established by using SolidWorks (Dassault Systemes, S.A, Paris, France). Tetrahedral mesh models were established by using Workbench (Ansys; Pittsburgh, PA, USA). The model was named model A. Similarly, model B was constructed. The model was then reimported into the Mimics program. The plane mesh models were divided and smoothed. By doing so, two 3D finite element models of model A and model B were established (Figure 3).
When a healthy adult weighing 60 kg is standing, the pressure on the tibial plateau is 60 kg × 9.8 N/kg × 85.6% 503.33 N. The force exerted on the tibial plateau by people when walking and running is about 2 times and 3 times as much as that when standing, respectively (12). A previous study showed that about 99% of splitting or collapse of TPF occur due to axial stress (13). Most people’s daily activities involve standing, walking, and running. Therefore, in this study, 3 levels of axial loads, including 500, 1,000, and 1,500 Newton (N), were selected to simulate the stress conditions for the tibial plateau when adult people stand, walk, and run, respectively. Of this, the lateral platform bears about 40% of the stress (14). The displacement of the bone mass under load <2 mm is generally considered to be effective (15). In this study, the screw and gasket were simplified to be a whole one, and threaded screws were simplified to be smooth screws, which could better highlight the role of steel plates. The maximum stress, maximum displacement, and maximum strain of the fracture block and internal fixation were obtained according to different stress conditions, and a complete report was generated. The stress, deformation, and strain nephograms of the two finite element models were analyzed under three loading conditions (standing, walking, and running).
Results
To support posterolateral fractures of the tibial plateau, Ren et al. (5,7) invented a new type of rotary support plate and improved its biomechanical performance with the assistance of imaging measurements. Kfuri et al. (8) and Chen et al. (9) reported that the posterolateral fracture often occurs in conjunction with a lateral split bone. However, this type of fracture was not included in the mechanical study on the new steel plate by Ren et al. (5,7). To improve the mechanical study on the new steel plate, the supportive effect of the new steel plate on the lateral bone mass was evaluated using finite element (FEA) analysis for the maximum displacement, maximum stress, and maximum strain of the fracture and internal fixation.
Model A (two tensile screws fix the fractured block and then hold it firmly with new steel plate pressurization) and model B (two tensile screws hold the fracture block in place. The FEA results are shown in the Figures 4-6 and sorted in Tables 1,2.

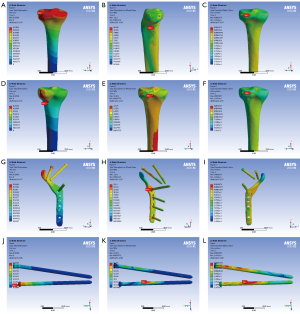
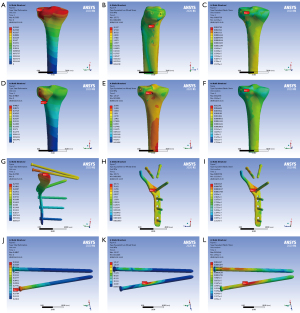
Table 1
| Max data | 500 N | 1,000 N | 1,500 N | |||||
|---|---|---|---|---|---|---|---|---|
| Model A | Model B | Model A | Model B | Model A | Model B | |||
| Max displacement (mm) | 0.085797 | 0.15675 | 0.17043 | 0.29868 | 0.25465 | 0.44017 | ||
| Max stress (Mpa) | 11.285 | 6.5519 | 20.648 | 12.575 | 29.227 | 18.842 | ||
| Max strain (mm) | 0.0012474 | 0.0032554 | 0.0074357 | 0.0074357 | 0.0035769 | 0.012146 | ||
Table 2
| Max data | 500 N | 1,000 N | 1,500 N | |||||
|---|---|---|---|---|---|---|---|---|
| Model A | Model B | Model A | Model B | Model A | Model B | |||
| Max displacement (mm) | 0.096932 | 0.14177 | 0.18682 | 0.27109 | 0.27655 | 0.39849 | ||
| Max stress (Mpa) | 69.54 | 48.916 | 112.1 | 92.251 | 155.71 | 135.27 | ||
| Max strain (mm) | 0.00066228 | 0.00046608 | 0.0010676 | 0.00087893 | 0.0014829 | 0.0012887 | ||
Discussion
Lateral bone mass displacement
The data in the present study showed that at all three load levels, the bone displacement in model A (Figure 3, Model A) was smaller than that in model B (Figure 3, Model B), and the displacement in the model A steel plate was smaller than that in model B, while the maximum displacements in models A and B were both less than 2 mm. These results demonstrated that the two fixation methods were able to fix this type of fracture, and the displacement of the lateral bone mass was obviously reduced under the action of the new steel plate, indicating that the new steel plate has a good supportive effect on the lateral bone mass. At the same time, the internal fixation mode of model A is more stable than that of model B. Under three distinct loads, the maximum displacement of the new steel plate is smaller than that of the bone mass, indicating that the new steel plate can stabilize the fractured bone. The maximum displacement was at the articular surface of the tibial plateau and posterolateral split bone in model A, while it was at the bottom of the lateral bone mass in model B. This is likely due to the force at the bottom of the lateral bone mass being offset by the steel plate when the load was applied. Since the maximum collapse displacement was much less than 2 mm, the effect of this collapse on the articular surface was deemed negligible.
The maximum stress of the model
Under the three distinct loads, the pressure of model A was greater than that of model B, and the maximum stress of the two models under these loads was greater than that in the bone trabeculae but less than that of the normal tibia in the human body (16-18). Therefore, we suggest that patients treated by the two fixation methods should avoid strenuous exercise after surgery as to prevent trabecular microfractures. According to Wolff’s law and the promoting factors of callus healing, the pressure of model A is slightly higher than that of model B, indicating the mechanical stimulation of model A is stronger than that of model B, which is very important in late fracture healing and callus plasticity (19). Rogge et al. suggested that the more uniform the stress distribution in the fracture site is, the more beneficial to the fracture healing it will be (20). In this study, the stress distribution in model A was more uniform in both the fracture and internal fixation, while the stress in model B was more concentrated. In this case, model B is more prone to microfractures under the action of shear forces, which may lead to internal fixation fatigue and even screw breakage. At the same time, the maximum stress of the steel plate and screw is much less than the maximum yield strength of titanium alloy at 795 Mpa (17,21). This suggested that, to a certain extent, the new steel plate satisfies the normal activities of the human body.
The maximum strain of the model
The maximum strain of the two models under the three distinct loads were all distributed at the broken end of the fracture. The maximum strain of internal fixation in model A was greater than that in model B at 1,000 and 1,500 N, but smaller than that in model B at 500 N. This is caused by the stress concentrated at the sharp contact point between the plate screw and the steel plate of model A, that is, the stress concentrated at the screw contact plate at the root of the screw. From the strain distribution diagram, it was clear that the fixation combination of model A shared more axial load. According to Perren’s strain theory, the stress shielding effect of the plates in model A is less than that in model B, indicating that the fixation mode in model A is more conducive to fracture healing (22,23). Model A has more stress shielding effect: for this fracture, some difference of stress shielding effect is not important as the fracture area is metaphysis not diaphysis. Healing potential is high in metaphysis, so secure fixation is important. Therefor model A is excellent method. The maximum strain of internal fixation in model A was concentrated at the straight plate which supports the lateral bone mass, indicating that the new steel plate has an obvious supportive effect on the lateral sides of the fracture, and this effect may promote fracture healing.
In order to better treat this type of fracture, most scholars have focused on studying surgical approaches such as the anterolateral approach, the posterior medial approach, and the fibular osteotomy and the modified posterior lateral approach (24-26). The traditional surgical approach produces poor surgical field and tends to lead to difficulties in fixation, with the resulting problem of inadequate knee stability.
We encountered some limitations in the analysis of our results. First, the finite element method used to simulate the three load levels was based on an ideal condition, which might not truly represent the actual movement, and did not include the impact of the soft tissue around the knee joint on the model. Second, this study mainly focused on the supportive effect of the new type of steel plate on the lateral bone mass, and did not involve the collapse of the articular surface of the tibial plateau. For lateral TPF with articular surface collapse, the supportive effect of ARSP on the lateral bone mass warrants further investigation.
Conclusions
By examining the maximum displacement, maximum stress, and maximum strain of the fracture block, we demonstrated that ARSP has supportive effects on the lateral bone mass. For complex TPF with posterolateral and lateral TPF without collapse, both methods including simple screw fixation and new plate plus screw fixation can achieve satisfactory fixation effects. Model A fixation strengthens the supportive effect of the lateral bone mass, therefore, the fixation works better. The fixed mode of model A can be completed with one incision. Compared with the traditional L-shaped plate with posterior plate and other fixation methods, the new plate with screw fixation method is easier to handle, less invasive, and more affordable. Given the data from the maximum displacement in the two models, we are confident that the new plates can be fixed with screws when dealing with complex TPF, which not only reduces the cost to patients, but also avoids large areas of soft tissues peeling as a result of the placement of the L-shaped plate.
The artificial tibia model is widely used in the field of biomechanical research, but his data of bone density, compression deformation and fractional friction coefficient are still slightly different from those of fresh human tibia specimens. In addition, our simulated fracture model does not take into account the tissues surrounding the knee joint, including the medial and lateral collateral ligaments, meniscus, nerves and accompanying blood vessels, and other factors that may affect the actual outcome. All these factors need to be further explored.
Acknowledgments
The authors appreciate the academic support from the AME Orthopaedic Surgery Collaborative Group.
Funding: None.
Footnote
Reporting Checklist: The authors have completed the MDAR reporting checklist. Available at https://atm.amegroups.com/article/view/10.21037/atm-22-4529/rc
Data Sharing Statement: Available at https://atm.amegroups.com/article/view/10.21037/atm-22-4529/dss
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://atm.amegroups.com/article/view/10.21037/atm-22-4529/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Piposar J, Fowler JR, Gaughan JP, et al. Race may not affect [correct] outcomes in operatively treated tibia fractures. Clin Orthop Relat Res 2012;470:1513-7. Erratum in: Clin Orthop Relat Res 2012;470:2058. [Crossref] [PubMed]
- Urruela AM, Davidovitch R, Karia R, et al. Results following operative treatment of tibial plateau fractures. J Knee Surg 2013;26:161-5. [Crossref] [PubMed]
- Salduz A, Birisik F, Polat G, et al. The effect of screw thread length on initial stability of Schatzker type 1 tibial plateau fracture fixation: a biomechanical study. J Orthop Surg Res 2016;11:146. [Crossref] [PubMed]
- Carrera I, Gelber PE, Chary G, et al. Fixation of a split fracture of the lateral tibial plateau with a locking screw plate instead of cannulated screws would allow early weight bearing: a computational exploration. Int Orthop 2016;40:2163-9. [Crossref] [PubMed]
- Ren D, Liu Y, Chen Y, et al. A Novel Method of the Treatment for Posterolateral Tibial Plateau Fractures. J Knee Surg 2020;33:1010-9. [Crossref] [PubMed]
- Ren D, Liu Y, Zhou B, et al. A Novel Design of a Plate for Posterolateral Tibial Plateau Fractures Based on Computed Tomography Mapping of the Proximal Tibiofibular Joint. Med Sci Monit 2018;24:9300-6. [Crossref] [PubMed]
- Ren D, Liu Y, Lu J, et al. A Novel Design of a Plate for Posterolateral Tibial Plateau Fractures Through Traditional Anterolateral Approach. Sci Rep 2018;8:16418. [Crossref] [PubMed]
- Kfuri M, Schatzker J. Revisiting the Schatzker classification of tibial plateau fractures. Injury 2018;49:2252-63. [Crossref] [PubMed]
- Chen P, Shen H, Wang W, et al. The morphological features of different Schatzker types of tibial plateau fractures: a three-dimensional computed tomography study. J Orthop Surg Res 2016;11:94. [Crossref] [PubMed]
- Zhang W, Luo CF, Putnis S, et al. Biomechanical analysis of four different fixations for the posterolateral shearing tibial plateau fracture. Knee 2012;19:94-8. [Crossref] [PubMed]
- Hu P, Wu T, Wang HZ, et al. Influence of Different Boundary Conditions in Finite Element Analysis on Pelvic Biomechanical Load Transmission. Orthop Surg 2017;9:115-22. [Crossref] [PubMed]
- Tai CL, Chen WP, Chen HH, et al. Biomechanical optimization of different fixation modes for a proximal femoral L-osteotomy. BMC Musculoskelet Disord 2009;10:112. [Crossref] [PubMed]
- Horwitz DS, Bachus KN, Craig MA, et al. A biomechanical analysis of internal fixation of complex tibial plateau fractures. J Orthop Trauma 1999;13:545-9. [Crossref] [PubMed]
- Raja Izaham RM, Abdul Kadir MR, Abdul Rashid AH, et al. Finite element analysis of Puddu and Tomofix plate fixation for open wedge high tibial osteotomy. Injury 2012;43:898-902. [Crossref] [PubMed]
- Haller JM, O'Toole R, Graves M, et al. How much articular displacement can be detected using fluoroscopy for tibial plateau fractures? Injury 2015;46:2243-7. [Crossref] [PubMed]
- Goldstein SA, Wilson DL, Sonstegard DA, et al. The mechanical properties of human tibial trabecular bone as a function of metaphyseal location. J Biomech 1983;16:965-9. [Crossref] [PubMed]
- Boluda-Mengod J, Guimerà-García V, Olías-López B, et al. A proposal of a new algorithm for decision-making approaches in open reduction and internal fixation of complex tibial plateau fractures - SOTA algorithm (Spanish Orthopaedic Trauma Association). Injury 2021;52:S87-98. [Crossref] [PubMed]
- Phillips SA, Comadoll SM, Hautala GS, et al. Newer generation of proximal tibia locking plates demonstrate large variability in their ability to capture the posteromedial fragment in bicondylar tibial plateau fractures. Injury 2021;52:1534-8. [Crossref] [PubMed]
- Camal Ruggieri IN, Cícero AM, Issa JPM, et al. Bone fracture healing: perspectives according to molecular basis. J Bone Miner Metab 2021;39:311-31. [Crossref] [PubMed]
- Rogge RD, Adams BD, Goel VK. An analysis of bone stresses and fixation stability using a finite element model of simulated distal radius fractures. J Hand Surg Am 2002;27:86-92. [Crossref] [PubMed]
- Tian L, Sheng Y, Huang L, et al. An innovative Mg/Ti hybrid fixation system developed for fracture fixation and healing enhancement at load-bearing skeletal site. Biomaterials 2018;180:173-83. [Crossref] [PubMed]
- Glatt V, Evans CH, Tetsworth K. Reverse dynamisation: a modern perspective on Stephan Perren's strain theory. Eur Cell Mater 2021;41:668-79. [Crossref] [PubMed]
- Lambert S, Mischler D, Windolf M, et al. From creative thinking to scientific principles in clinical practice. Injury 2021;52:32-6. [Crossref] [PubMed]
- Tosounidis TH, Giannoudis PV. Letter to the Editor: "A combined posterior reversed L-shaped and anterolateral approach for two column tibial plateau fractures in Caucasians: A technical note". Injury 2016;47:983.
- Jiwanlal A, Jeray KJ. Outcome of Posterior Tibial Plateau Fixation. J Knee Surg 2016;29:34-9. [Crossref] [PubMed]
- Yu B, Han K, Zhan C, et al. Fibular head osteotomy: a new approach for the treatment of lateral or posterolateral tibial plateau fractures. Knee 2010;17:313-8. [Crossref] [PubMed]


