Development of a normal tissue complication probability (NTCP) model using an artificial neural network for radiation-induced necrosis after carbon ion re-irradiation in locally recurrent nasopharyngeal carcinoma
Introduction
The main goal of radiotherapy is to kill tumor cells effectively, as well as avoid damaging normal tissues. Normal tissue complication probability (NTCP) is a significant index to assess the likelihood of radiation-induced injuries to normal organ and plays an important role in treatment planning and decision making. Since early complication factor research (1), studies on normal tissue complication probability have mainly focused on building a mathematical model to describe the dose response and radiobiologic mechanism. Of these models, the most accepted is the Lyman-Kutcher-Burman model (2-6), which is now used by various treatment planning systems (TPS). It uses the dose-volume histogram (DVH) reduction method to simplify non-uniform dose distributions into uniform ones, which could be compared to existing data to calculate complication probability. Different from Lyman-Kutcher-Burman model, the Källman model (7) calculates the response of single cells first, and combines the response of cells to obtain the final NTCP. While those two models are not based on any biophysical background, the Niemierko model (8) is built usng linear-quadratic model, the best-known cell-killing model. In addition, since it takes into consideration the differrence of radiation sensitivity among organs and cohorts, Niemierko model is able to calculate the NTCP over the patient population. However, later studies have revealed that DVH is not the only factor to predict NTCP. Therefore, a model using both dosimetric data and patient characteristics is required for a more accurate prediction. The development of machine learning has enabled the combination of these factors. Through the numerical scoring of plans and predicting the likelihood of a certain complication (9-15), the feasibility and generalizability of machine learning in NTCP research have been confirmed.
An NTCP model for carbon therapy is necessary, as traditional NTCP models are based on photon irradiation. Due to different radiobiologic effects, applying these models to carbon therapy directly may be inappropriate. There are some methods to transfer the doses of carbon therapy to those of photon therapy, but an NTCP model for carbon therapy specifically has not been built yet, to the best of our knowledge.
The aim of the present study was to build an NTCP model for predicting mucosal necrosis after carbon therapy of locally recurrent nasopharyngeal carcinoma (rNPC) using a 2-layer artificial neural network (ANN). Both dosimetric and non-dosimetric data were used to build the model. Compared with previously published models, there are some changes we have made. On the one hand, since no NTCP model has been built for carbon re-irradiation, our model might be the first one for carbon therapy. On the other hand, whereas previous studies that only focused on patients without re-irradiation, our model has included dose of initial treatment and demonstrated its correlation with mucosal necrosis. We present the following article in accordance with the TRIPOD reporting checklist (available at https://atm.amegroups.com/article/view/10.21037/atm-20-7805/rc).
Methods
Patient and treatment data
Follow-up data and treatment plans of 214 rNPC patients treated with carbon therapy at Shanghai Proton and Heavy Ion Center from 2015 to 2019 were collected for the present study. The inclusion criteria were as follows: (I) initial treatment data were available; (II) no T0N1 stage; and (III) all the plans shared the same contouring file. In total, 150 patients were finally enrolled in the study. Patient characteristics are given in Table 1.
Table 1
| Patient character | Range | Mean |
|---|---|---|
| Sex | ||
| Male | 109 | |
| Female | 41 | |
| Age at initial treatment (years) | 15.7–64.4 | 45.6 |
| Initial stage | ||
| I | 0 | |
| II | 16 | |
| III | 68 | |
| IV | 40 | |
| NA | 26 | |
| Initial treatment technique | ||
| IMRT | 145 | |
| Non-IMRT | 5 | |
| Initial treatment dose (Gy) | 34–60 | 45.5 |
| Initial treatment fraction | 30–38 | 32.4 |
| Induction chemotherapy of initial treatment | ||
| Yes | 24 | |
| No | 126 | |
| Disease-free interval (months) | 39.0–89.7 | 80.5 |
| Age at recurrent treatment (years) | 17.0–68.7 | 49.1 |
| Final pathology | ||
| NKU | 107 | |
| NKD | 20 | |
| SCC | 21 | |
| NA | 2 | |
| Recurrent stage | ||
| I | 7 | |
| II | 40 | |
| III | 49 | |
| IV | 54 | |
| Baseline necrosis | ||
| Yes | 42 | |
| No | 108 | |
| Concurrent chemotherapy | ||
| Yes | 33 | |
| No | 117 | |
IMRT, intensity-modulated radiation therapy; NA, not available; NKD, non-keratinizing differentiated; NKU, non-keratinizing undifferentiated; SCC, squamous cell carcinoma.
Recurrent treatment plan data were obtained from TPS. Patients were identified as positive when low intensity defects of mucosa were found enhanced magnetic resonance image. As no mucosa structure was contoured in the TPS, the DVH of PTV was exported as an alternative. Vx values of all the studied structures were calculated every 5 GyE from 5 to 50 GyE. As well as dosimetric variables, clinical factors from our follow-up database were also included in this study (Table 2). As the first 4 factors (core parameters) in Table 2 were considered important, according to the clinicians’ experience, they were fixed throughout the study, whereas the other factors were studied to determine the variable resulting in the best prediction. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by the Ethics Committee at Shanghai Proton and Heavy Ion Center (approval number: 2008-43-02). Written informed consent was obtained from all patients.
Table 2
| Variable | Description | Remark |
|---|---|---|
| T stage | T category of locally recurrent nasopharyngeal carcinoma | |
| tumor_vol | Volume of recurrent tumor (cm3) | |
| Interval | Time interval between initial treatment and recurrent treatment | |
| reRT_age | Age at recurrent radiotherapy | |
| body.Vx | Volume (cm3) inside outer contour receiving dose more than x GyE | x=5, 10, 15, …, 50 |
| bodyus.Vx | Volume (cm3) under sphenoid sinus receiving dose more than x GyE | x=5, 10, 15, …, 50 |
| PTV.Vx | Volume (cm3) of PTV receiving dose more than x GyE | x=5, 10, 15, …, 50 |
| Gender | Sex of patient | |
| BED1 | Biologically equivalent dose of initial treatment | α/β=3 |
| Baseline | Whether baseline necrosis exists before recurrent treatment | |
| necro_loc | Location of baseline necrosis before recurrent treatment | Used with baseline |
| BED2 | Biologically equivalent dose of recurrent treatment | α/β=3 |
PTV, planning target volume.
Statistical analysis
T-test was performed to compare the distribution of age at recurrent treatment, BED of initial treatment and recurrent treatment, while t-test was conducted to compare the distribution of other variables shown in Table 1.
ANN
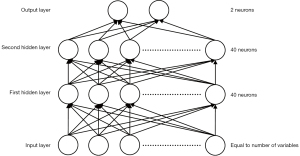
As suggested by Heckerling et al. (16), an ANN was constructed with 2 hidden layers, each containing 40 nodes (Figure 1). Variable values were normalized to the distribution, with an average of 0 and standard deviation of 1, before being input into the network. During the training process, stochastic gradient descent with momentum was used to optimize the model, and 10-fold cross-validation was conducted to evaluate the prediction performance. Due to the data-dependent nature of an ANN, groups were divided randomly using different seeds to minimize the influence of outliers, and the final performance was calculated by averaging all the results. The hyperparameters used are listed in Table 3. Due to an imbalanced positive-negative ratio (32:118), simple oversampling was used in the training process. Overall accuracy and AUC were obtained to evaluate prediction performance.
Table 3
| Hyperparameter | Value |
|---|---|
| Learning rate | 0.2 |
| Momentum | 0.9 |
| Number of hidden layers | 2 |
| Number of nodes in each hidden layer | 40 |
| Epoch | 10,000 |
| Batch size | 32 |
Results
DVH parameters
The overall accuracy of different DVH parameters combined with core parameters ranged between 73.2% and 81.9% on the training set, and between 58.3% and 65.2% on the validation set (Table 4). In general, DVH parameters of PTV give a higher prediction accuracy than that of other regions. Of all the parameters PTV.V25 had the best predictive factor. Interestingly, although using all DVH parameters of a region of interest has better prediction results than using no DVH parameter, it is not even better than the best single factor. In addition, the DVH of PTV is the most predictive, on average.
Table 4
| Parameter | Training set | Validation set | |||||||
|---|---|---|---|---|---|---|---|---|---|
| TPR (%) | TNR (%) | Accuracy (%) | AUC | TPR (%) | TNR (%) | Accuracy (%) | AUC | ||
| PTV.Vx | |||||||||
| PTV.V5 | 79.3 | 76.3 | 77.9 | 0.757 | 52.2 | 65.8 | 62.9 | 0.614 | |
| PTV.V10 | 78.7 | 75.6 | 77.2 | 0.768 | 53.3 | 67.3 | 64.3 | 0.642 | |
| PTV.V15 | 78.3 | 74.8 | 76.7 | 0.758 | 50 | 67.3 | 63.6 | 0.635 | |
| PTV.V20 | 76.8 | 75.9 | 76.4 | 0.761 | 47.8 | 66.7 | 62.60 | 0.636 | |
| PTV.V25 | 77.3 | 75.2 | 76.3 | 0.751 | 53.3 | 68.5 | 65.2 | 0.659 | |
| PTV.V30 | 78.8 | 76 | 77.5 | 0.749 | 52.2 | 66.7 | 63.6 | 0.637 | |
| PTV.V35 | 78.9 | 77.1 | 78.1 | 0.76 | 53.3 | 67 | 64 | 0.637 | |
| PTV.V40 | 79.7 | 76.5 | 78.2 | 0.752 | 50 | 67.9 | 64 | 0.636 | |
| PTV.V45 | 82.6 | 74.5 | 78.8 | 0.746 | 52.2 | 64.2 | 61.7 | 0.64 | |
| PTV.V50 | 71.9 | 74.7 | 73.2 | 0.738 | 48.9 | 67 | 63.1 | 0.64 | |
| None | 76.9 | 69 | 73.2 | 0.742 | 48.9 | 60.9 | 58.3 | 0.548 | |
| All | 70.8 | 76.5 | 73.5 | 0.783 | 50 | 69.1 | 65 | 0.641 | |
| Body.Vx | |||||||||
| Body.V5 | 88 | 74.1 | 81.3 | 0.751 | 54.4 | 65.2 | 62.9 | 0.643 | |
| Body.V10 | 85.5 | 77.9 | 81.9 | 0.759 | 52.2 | 65.5 | 62.6 | 0.633 | |
| Body.V15 | 85.3 | 77.7 | 81.6 | 0.756 | 53.3 | 66.4 | 63.6 | 0.604 | |
| Body.V20 | 84 | 75.4 | 79.9 | 0.735 | 52.2 | 64.8 | 62.1 | 0.618 | |
| Body.V25 | 80.5 | 78.2 | 79.4 | 0.747 | 46.7 | 66.1 | 61.9 | 0.589 | |
| Body.V30 | 82.6 | 75.2 | 79.1 | 0.753 | 46.7 | 65.8 | 61.7 | 0.648 | |
| Body.V35 | 83.9 | 73.9 | 79.1 | 0.749 | 51.1 | 66.4 | 63.1 | 0.617 | |
| Body.V40 | 84.6 | 72.1 | 78.6 | 0.755 | 53.3 | 65.2 | 62.6 | 0.634 | |
| Body.V45 | 82.4 | 75.8 | 79.3 | 0.75 | 48.9 | 68.8 | 64.5 | 0.626 | |
| Body.V50 | 84.7 | 74.4 | 79.7 | 0.73 | 53.3 | 63.6 | 61.4 | 0.61 | |
| None | 76.9 | 69 | 73.2 | 0.742 | 48.9 | 60.9 | 58.3 | 0.548 | |
| All | 76.8 | 76.9 | 76.8 | 0.771 | 47.8 | 68.8 | 64.3 | 0.622 | |
| Bodyus.Vx | |||||||||
| Bodyus.V5 | 84.6 | 76.8 | 80.9 | 0.745 | 44.4 | 66.1 | 61.4 | 0.599 | |
| Bodyus.V10 | 87.4 | 73.4 | 80.6 | 0.745 | 51.1 | 62.4 | 60 | 0.628 | |
| Bodyus.V15 | 84.1 | 74 | 79.3 | 0.737 | 45.6 | 66.1 | 61.7 | 0.596 | |
| Bodyus.V20 | 82.2 | 77.1 | 79.7 | 0.746 | 46.7 | 68.5 | 63.8 | 0.615 | |
| Bodyus.V25 | 83.2 | 77.7 | 80.6 | 0.757 | 45.6 | 67.6 | 62.9 | 0.593 | |
| Bodyus.V30 | 84.4 | 76.9 | 80.8 | 0.756 | 51.1 | 64.5 | 61.7 | 0.581 | |
| Bodyus.V35 | 85.2 | 73.4 | 79.5 | 0.746 | 52.2 | 63.3 | 61 | 0.597 | |
| Bodyus.V40 | 85.5 | 74.7 | 80.3 | 0.75 | 48.9 | 63.3 | 60.2 | 0.604 | |
| Bodyus.V45 | 85.9 | 74.4 | 80.4 | 0.746 | 53.3 | 64.8 | 62.4 | 0.61 | |
| Bodyus.V50 | 85.1 | 73.8 | 79.6 | 0.752 | 51.1 | 62.4 | 60 | 0.581 | |
| None | 76.9 | 69 | 73.2 | 0.742 | 48.9 | 60.9 | 58.3 | 0.548 | |
| All | 82.3 | 81.9 | 82.1 | 0.769 | 40 | 67.9 | 61.9 | 0.574 | |
None: no DVH parameter was used in the model; all: all DVH parameters were used in the model. PTV, planning target volume; TPR, true positive rate; TNR, true negative rate; AUC, area under receiver operating curve; DVH, dose-volume histogram.
Clinical parameters
As PTV.V25 was found to be the best predictor in the previous step where different DVH parameters were studied, it was fixed with core parameters in this step. Different clinical factors were included in the model to see how they could improve prediction accuracy. The results showed that most clinical parameters could increase accuracy, except location of baseline necrosis (necro_loc) and biologically equivalent dose of recurrent therapy (BED2) (Table 5). Of these factors, biologically equivalent dose of initial therapy (BED1) was the most effective, with an increase of 1.5%, but with a decrease in true positive rate (TPR).
Table 5
| Parameter | Training set | Validation set | |||||||
|---|---|---|---|---|---|---|---|---|---|
| TPR (%) | TNR (%) | Accuracy (%) | AUC | TPR (%) | TNR (%) | Accuracy (%) | AUC | ||
| Baseline | 82.8 | 80.3 | 81.6 | 0.802 | 42.2 | 72.1 | 65.7 | 0.638 | |
| Baseline + necro_loc | 87.4 | 73.4 | 80.6 | 0.745 | 51.1 | 62.4 | 60.0 | 0.628 | |
| Sex | 83.7 | 81.2 | 82.5 | 0.766 | 53.3 | 69.1 | 65.7 | 0.642 | |
| BED1 | 87.7 | 79.9 | 84.0 | 0.783 | 50.0 | 71.2 | 66.7 | 0.689 | |
| BED2 | 85.2 | 78.6 | 82.0 | 0.772 | 46.7 | 67.8 | 63.3 | 0.651 | |
| None | 77.3 | 75.2 | 76.3 | 0.751 | 53.3 | 68.5 | 65.2 | 0.659 | |
| All | 83.9 | 86.4 | 85.1 | 0.807 | 40.0 | 73.3 | 66.2 | 0.582 | |
None: no clinical parameter was used in the model; all: all clinical parameters were used in the model. BED, biologically equivalent dose; TPR, true positive rate; TNR, true negative rate; AUC, area under receiver operating curve.
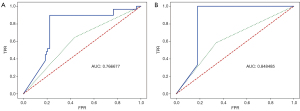
The most predictive parameters in the present study were T stage, tumor_vol, interval, reRT_age, PTV.V25, and BED1. The receiver-operating characteristic (ROC) curve of the final model using these parameters is shown in Figure 2. As no data were available for external validation, only the best (not average) performance was shown.
Discussion
Although no sampling algorithm had a significant advantage in Gabryś’s study (17), sampling was confirmed necessary in the present study, or the network would classify all data into the majority group. Classifying all data into the majority group could result in better accuracy (80%), but this is meaningless for NTCP prediction. Therefore, in the training process, data from the minority group (positive group) was copied 4 times, so that data the data in both groups had approximately the same volume. Additionally, overall accuracy should not be the only standard to evaluate an NTCP model, and other indexes, such as the confusion matrix and the ROC curve, should also be studied for a comprehensive evaluation.
Another condition that should be considered is the random division of data according to ratio. For example, if the network divides the data into the negative group for 80% of situations and the positive group for the other 20% of situation, then the accuracy = 80%×80%+20%×20%=68%, but will have a poor TPR of 20%. As the TPR of the validation set shows, the network also succeeded in avoiding such classification.
The clinical factor test results showed that baseline necrosis and sex can slightly improve prediction accuracy. Conventionally, sex is considered a questionable variable, whereas the odds ratio of sex was >2.5 in our study cohort. Further study is necessary to demonstrate whether this is due to the imbalanced distribution of sex. The BED of initial treatment was found to be the most effective factor to increase predictivity, which confirmed our hypothesis. This suggests that the condition of initial treatment may need to be included in NTCP research of re-irradiation.
Due to the data-driven nature of an ANN, the accuracy of this model was <70%, partly because data distributions of both the positive and negative groups were quite similar (Figure 3). Therefore, the best prediction accuracy, 66.7%, might be seen as an acceptable model for these data. More “typical” and “separable” data are required to build a model with higher accuracy. Additionally, it remains to be studied whether the hyperparameters used in this model are the optimal ones. In order to improve the performance of our model, further study might focus on the changes of prediction accuracy over a series of network structures and input parameters.

Finally, as a result of the “black-box” character of an ANN, only factors that were considered important were analyzed in the present study. More efforts are needed to determine the specific correlation within variables and between variables and results, and to build the ideal model using the best variable group as inputs. This model is only the first and a small step in NTCP research in carbon ion therapy and re-irradiation, but more complete models should emerge in the future.
Conclusions
An ANN was built for the prediction of radiation-induced necrosis after carbon ion re-irradiation in rNPC. Of the DVH parameters, PTV.V25 was found to be the most predictive, with an accuracy of 65.2%. Of the clinical parameters, baseline necrosis, sex, and BED of initial treatment were found to increase the prediction accuracy of PTV.V25 by 0.5–1.5%.
Acknowledgments
Funding: The present study was supported by the Joint Breakthrough Project for New Frontier Technologies of the Shanghai Hospital Development Center (Project No. SHDC12019120); Science and Technology Commission of Shanghai Municipality (Project No. 1941951000).
Footnote
Reporting Checklist: The authors have completed the TRIPOD reporting checklist. Available at https://atm.amegroups.com/article/view/10.21037/atm-20-7805/rc
Data Sharing Statement: Available at https://atm.amegroups.com/article/view/10.21037/atm-20-7805/dss
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://atm.amegroups.com/article/view/10.21037/atm-20-7805/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by the Ethics Committee at Shanghai Proton and Heavy Ion Center (approval number: 2008-43-02). Written informed consent was obtained from all patients.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Wolbarst AB, Sternick ES, Curran BH, et al. A FORTRAN program for the optimization of radiotherapy treatment planning using the complication probability factor (CPF). Comput Programs Biomed 1980;11:99-104. [Crossref] [PubMed]
- Lyman JT. Complication probability as assessed from dose-volume histograms. Radiat Res Suppl 1985;8:S13-9. [Crossref] [PubMed]
- Lyman JT, Wolbarst AB. Optimization of radiation therapy, III: A method of assessing complication probabilities from dose-volume histograms. Int J Radiat Oncol Biol Phys 1987;13:103-9. [Crossref] [PubMed]
- Kutcher GJ, Burman C. Calculation of complication probability factors for non-uniform normal tissue irradiation: the effective volume method. Int J Radiat Oncol Biol Phys 1989;16:1623-30. [Crossref] [PubMed]
- Kutcher GJ, Burman C, Brewster L, et al. Histogram reduction method for calculating complication probabilities for three-dimensional treatment planning evaluations. Int J Radiat Oncol Biol Phys 1991;21:137-46. [Crossref] [PubMed]
- Lyman JT, Wolbarst AB. Optimization of radiation therapy, IV: A dose-volume histogram reduction algorithm. Int J Radiat Oncol Biol Phys 1989;17:433-6. [Crossref] [PubMed]
- Jackson A, Kutcher GJ, Yorke ED. Probability of radiation-induced complications for normal tissues with parallel architecture subject to non-uniform irradiation. Med Phys 1993;20:613-25. [Crossref] [PubMed]
- Niemierko A, Goitein M. Modeling of normal tissue response to radiation: the critical volume model. Int J Radiat Oncol Biol Phys 1993;25:135-45. [Crossref] [PubMed]
- Willoughby TR, Starkschall G, Janjan NA, et al. Evaluation and scoring of radiotherapy treatment plans using an artificial neural network. Int J Radiat Oncol Biol Phys 1996;34:923-30. [Crossref] [PubMed]
- Gulliford SL, Webb S, Rowbottom CG, et al. Use of artificial neural networks to predict biological outcomes for patients receiving radical radiotherapy of the prostate. Radiother Oncol 2004;71:3-12. [Crossref] [PubMed]
- Chen S, Zhou S, Yin FF, et al. Investigation of the support vector machine algorithm to predict lung radiation-induced pneumonitis. Med Phys 2007;34:3808-14. [Crossref] [PubMed]
- Pella A, Cambria R, Riboldi M, et al. Use of machine learning methods for prediction of acute toxicity in organs at risk following prostate radiotherapy. Med Phys 2011;38:2859-67. [Crossref] [PubMed]
- Oh J, Wang Y, Apte A, et al. SU-E-T-259: A Statistical and Machine Learning-Based Tool for Modeling and Visualization of Radiotherapy Treatment Outcomes. Med Phys 2012;39:3763. [Crossref] [PubMed]
- Kang J, Schwartz R, Flickinger J, et al. Machine Learning Approaches for Predicting Radiation Therapy Outcomes: A Clinician's Perspective. Int J Radiat Oncol Biol Phys 2015;93:1127-35. [Crossref] [PubMed]
- Dean J, Wong K, Gay H, et al. Incorporating spatial dose metrics in machine learning-based normal tissue complication probability (NTCP) models of severe acute dysphagia resulting from head and neck radiotherapy. Clin Transl Radiat Oncol 2018;8:27-39. [Crossref] [PubMed]
- Heckerling PS, Gerber BS, Tape TG, et al. Use of genetic algorithms for neural networks to predict community-acquired pneumonia. Artif Intell Med 2004;30:71-84. [Crossref] [PubMed]
- Gabryś HS, Buettner F, Sterzing F, et al. Design and Selection of Machine Learning Methods Using Radiomics and Dosiomics for Normal Tissue Complication Probability Modeling of Xerostomia. Front Oncol 2018;8:35. [Crossref] [PubMed]