Challenges and opportunities in biomarker-driven trials: adaptive randomization
Introduction
Genomics and molecular biology have been revolutionized to interrogate human disease biology. It results in an extensive range of tools developed such as whole genome or exome sequencing and multi-omics technologies (1,2). With the increased availability in advanced technology, more opportunities for prevention and therapy at the individual patient level are opened by the promise of personalized medicine. For example, Tabrecta, approved on May 6, 2020 by FDA under fast track, breakthrough therapy, accelerated approval, and priority review, is the first targeted therapy to treat patients with non-small cell lung cancer with mutations leading to MET exon 14 skipping. A next generation sequencing called the FoundationOne CDx assay (F1CDx) can detect the mutations leading to MET exon 14 skipping based in vitro diagnostic device and was approved by FDA as a companion diagnostic for Tabrecta.
To successfully and effectively translate the mechanistic findings through drug development process, it is critical to incorporate the biomarkers into clinical trials. Biomarker-driven clinical trials integrate clinical practice with clinical research under the precision medicine paradigm. The premise of precision medicine is that there is a subgroup of patients who benefit from the treatment, and the key is to enrich the trial population to optimize disease management and enhance efficiency. Therefore, it is necessary to develop statistical methods and designs to integrate biomarkers into the decision process and improve the clinical benefits of the targeted agents. Simon [2019] reviews the statistical methods for biomarker-driven clinical trials to deal with patient heterogeneity in the drug response (3). Optimal individualized treatment rules built on biomarkers identify a subgroup of patients who benefit from the experimental treatment and aid to determine personalized treatment decisions (4-9). Fixed or adaptive enrichment designs use the biomarkers in order to restrict enrollment to the patients who are expected to get more benefit from experimental treatment than the control, which magnifies the signal and improves the power to detect the treatment effect (10-16). Basket trials (e.g., NCI MATCH, NCI MPACT) or umbrella trials (e.g., BATTLE, I-SPY 2, Lung MAP) are implemented under the master protocol based on multiple tumor types for certain genetic mutations or different genetic mutations for a single type of tumor, respectively (17-22).
This paper aims to discuss challenges and opportunities in biomarker-driven randomization. The biomarker-driven randomization is a randomization strategy adapted based on biomarkers to identify patients who would respond better to the treatment and optimize the treatment allocation by adaptively randomizing more patients to the superior treatment based on biomarkers and accumulating information during the trial (23-28). We consider several types of biomarker-driven randomization, which are the covariate-adjusted versions of the existing response-adaptive randomization (RAR) and examine the performance of the covariate-adjusted RAR (CARA) in group sequential clinical trials allowing early stopping. We compare the biomarker-driven randomization with the traditional fixed randomization and RAR without incorporating biomarkers. We present the operating characteristics, such as rejection probability, estimated effect size at the final analysis, early stopping probability, the difference of the number of patients allocated to two treatments, and the number of failures, of the group sequential biomarker-driven trial designs through simulations and provide suggestions and considerations for the biomarker-driven randomization.
Biomarker-driven randomization in group sequential trials
In clinical trials, randomization is a typical strategy for removing potential bias and confounders in a patient group. Fixed randomization and adaptive randomization (e.g., response-adaptive randomization with/without using covariates) have been considered. Most clinical studies use fixed randomization, for example 1:1 or 2:1 is considered for two-arm randomized controlled trials (RCT), which means that the likelihood of individuals being randomly assigned to a treatment group remains constant throughout the trial. RCT with an equal allocation ratio randomizes the same number of patients to each treatment and yields a reasonable power to detect the treatment effect. However, RCT is criticized for ethical issues, and clinical investigators may deny RCT using the fixed randomization with an equal probability (29,30). They believe some patients with a particular type may not get potential benefits from the experimental treatment of interest against the control, and they do not want to randomize the patients without the restriction. To address the ethical issues of randomization and make more desirable in ethics, RAR is proposed to change a treatment allocation probability throughout the clinical trials and assign more patients to the treatment arm that is superior based on accumulating information. Specifically, for RAR in binary response experiments, Neyman allocation minimizes sample size (31), and Rosenberger et al. (32) proposes optimal allocation probability to minimize the expected number of failures. RAR is also implemented in the Bayesian framework (33,34). To incorporate patients’ biological covariates such as gene or protein expression, which may define the subset of patients who respond favorably to an experimental treatment, in RAR designs, CARA has been proposed. CARA estimates the response probability conditioning on the covariates for updating the treatment allocation probability (23-28). Thus, RAR and CARA designs increase ethically treating patients based on accumulating data (35-38). However, they require time to collect the results and update for future randomization and lead to bias due to temporal trends in the clinical trials (39-41).
We consider four different types of biomarker-driven randomization, which are the covariate-adjusted versions of the existing RAR method: Covariate-adjusted RAR 1 (CARA1) using the allocation ratio proposed in Thall et al. [2015] (41), Covariate-adjusted RAR 2 (CARA2) using the allocation ratio proposed in Rosenberger et al. [2001] (32), Covariate-adjusted RAR 3 (CARA3) using the allocation target proposed in Rosenberger et al. [2001] (23), and Covariate-adjusted RAR 4 (CARA4) using the Neyman allocation described in Mattew et al. [2013] (42). The allocation ratio used in CARA1 is employed in the Bayesian approach without incorporating biomarkers in Thall et al. [2015] (41), and the allocation ratios used in CARA2-CARA4 are commonly considered in frequentist approach in CARA designs without monitoring at interims. In the following paragraphs, we first describe the group sequential trial design which shows the design structure we used, and then CARA1-CARA4 are described with the formula under the group sequential design.
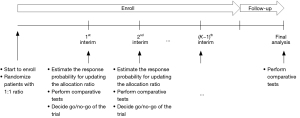
Suppose that we consider a two-arm comparative clinical trial with a maximum of N patients enrolled sequentially in K cohorts. The schema of the group sequential trial design is shown in Figure 1. The patients in the first cohort are equally randomized to either experimental treatment A or control B. When the first cohort’s patients are enrolled and complete the outcome evaluation, the biomarker-driven probability of randomization is built to identify the patients who are expected to get benefit more from A than B and update the allocation probability for the second cohort. Also, at the first interim, the comparative tests are performed to determine go or no-go of the trial, which allows the trial to be terminated due to either superiority or futility. If the trial does not stop early, then additional patients are enrolled in the second cohort and adaptively randomized to the best performing treatment based on the patients’ biomarker profile and accumulating data. This process is repeated sequentially until the end of the trial.
Let G be a treatment indicator taking 1 for receiving A and 0 for receiving B. Let Y be a binary response regarding 1 as a success event and 0 as a failure event. Let x be a p dimensional vector of biomarkers available at enrollment. Let denote the probability of response for the patient with the biomarker profile x who is receiving treatment A and denote the probability of response for the patient with the biomarker profile x who is receiving treatment B. For each k=1,2...,K−1, let Dk denote an accumulating data at the kth interim which is a set of Y, G, x over the k cohorts. Then four methods, CARA1-CARA4, define the following the biomarker-driven probability of randomization for the patient with a biomarker profile x in the kth cohort to the treatment A as
CARA1:
CARA2:
CARA3:
CARA4:
where , , and . The allocation probability of CARA1 uses the posterior probability denoted by hat treatment A has higher response rate for the patient with the biomarker profile x than treatment B based on accumulating data with k−1 cohorts. CARA2-CARA4 use the estimated response rate of treatment A and B denoted by and for the allocation, where they are obtained by the posterior probability of the response for the patient with the biomarker profile x who is receiving treatment A and B, respectively.
We assume a probit regression model for (x,G,Y) given by , where denotes the standard normal cumulative distribution function, , and and are the regression coefficient parameter vectors. Assuming normal priors on β and γ, the parameters are estimated by Bayesian posterior computation, i.e., the priors are used for the estimation of the posterior probabilities , , and .
An example using biomarker-driven randomization
To illustrate the application of biomarker-driven randomization, we consider stroke prevention in atrial fibrillation trials (43). The goal of the Stroke Prevention in Atrial Fibrillation (SPAF) study is to see how effective antithrombotic therapies are at preventing stroke in patients with nonvalvular atrial fibrillation. This was designed with RCT, but we use this study to provide how to re-design or use the biomarker-driven randomization. There are two arms for antithrombotic therapies such as warfarin (G=1, i.e., treatment arm A) and aspirin (G=0, i.e., treatment arm B). The binary response of success or failure denotes the absence of a stroke or the presence of a stroke. The SPAF study found that high-risk patients with atrial fibrillation get more benefit from warfarin against aspirin while the low-risk patients do not get benefit from warfarin compared to aspirin. Thus, the stroke risk subgroup (high and low) is a good biomarker. In addition, gender or age can be considered for designing the biomarker-driven trials because female patients are more likely to get benefit from the antithrombotic therapies than male patients and strokes are common in older adults with recurrent paroxysmal atrial fibrillation. Given the trial data, the parameter setting can be specified (i.e., true values of the regression coefficient can be estimated) and used for a preliminary simulation study.
Simulation study and results
We used computer simulations to evaluate the performance of the biomarker-driven randomization based on 1,000 replications. Each replication indicates a two-arm randomized clinical trial enrolling 210 patients. Our sample size of 210 (i.e., 105 patients per group) yielded 80% power to detect the difference of 0.2 with the significance level of 0.05 under the traditional randomized clinical trial using the fixed 1:1 randomization.
We considered two binary biomarkers x1 and x2 with values 1 (marker positive) or 0 (marker negative). Two biomarkers were independently generated from Bernoulli distributions with response probability P1 and P2, respectively. We considered P1=0.7,0.5,0.25 and P2=0.5 for the simulation study. We generated Y from a Bernoulli distribution with response probability given by
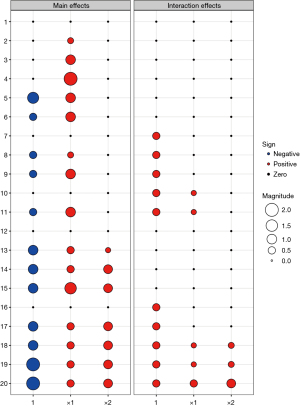
where G indicates the treatment indicator taking 1 for receiving A and 0 for receiving B, which is determined by the randomization methods. True model parameters are chosen to reflect patients’ heterogeneity and are described in Table 1. Figure 2 provides graphical presentations of the main effects and interaction effects of the intercept, x1 and x2 on the response for scenarios 1–20. Scenarios 1–6 and 12–15 indicate the null case where the response rate of patients receiving A is the same as the response rate of patients receiving B, i.e., no one gets benefit from the experimental treatment A against control B. Specifically, scenarios 1 and 12 have no any effect of biomarkers x1 and x2 and treatment G on the response, which describes the intercept only model for response probability, i.e., all patients have the same response rate regardless of patients’ biomarker profile or treatment assignment. However, scenarios 2–6 have a biomarker main effect β1; scenarios 2–4 result in overall response rate influenced by the first biomarker through β1=0.3,1,2 while scenarios 5-6 have an intercept effect through β0=−1.4,−0.5 as well as the effect of the first biomarker on the response (i.e., β1=1). Also, scenarios 13-15 have biomarker main effects β1 and β2 yielding the different response rate according to the biomarker profiles even though patients do not show difference between A and B. Scenarios 7–11 and 16–20 indicate the alternative case where the experimental treatment A has better efficacy in response than control B and there are some patients who get more benefit from A than B. Scenarios 7 and 16 have main experimental versus control effect γ0 but do not have any effect of informative biomarkers. Scenarios 8-9 have the main biomarker effect β1 additionally to the main experimental versus control effect γ0. Specifically, a prognostic biomarker x1 has a weak effect (i.e., β1=0.3) on response in scenario 8 while it has a relatively strong effect (i.e., β1=1) in scenario 9. Scenario 10 has no main biomarker effect but includes main experimental versus control effect γ0 and interaction effect between treatment group and the first biomarker γ1, i.e., this scenario does not consider any prognostic biomarker but consider predictive biomarker x1. In scenario 11, x1 plays a role in both prognostic and predictive biomarker. Moreover, scenarios 17–20 indicate the cases where patients’ responses are more heterogeneous compared to scenarios 8–11. Specifically, scenario 17 has two prognostic biomarkers x1 and x2 whose effects are so large that a certain subgroup x1=x2=1 yields a larger probability than the other subgroups regardless of the treatment assignment. In scenarios 18–20, both x1 and x2 are prognostic and predictive biomarkers. Compared to scenarios 18–19, scenario 20 has a relatively large effect of predictive biomarkers on the response so that patients receiving A show larger response than receiving B for the subgroup x1=x2=1.
Table 1
| Sc. | β0 | β1 | β2 | γ0 | γ1 | γ2 | (PA,PB) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| All patients | Patients with x1=1 | Patients with x1=0 | |||||||||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | (0.50, 0.50) | (0.50, 0.50) | (0.50, 0.51) | ||
| 2 | 0 | 0.3 | 0 | 0 | 0 | 0 | (0.56, 0.57) | (0.62, 0.63) | (0.50, 0.51) | ||
| 3 | 0 | 1 | 0 | 0 | 0 | 0 | (0.70, 0.70) | (0.85, 0.85) | (0.50, 0.51) | ||
| 4 | 0 | 2 | 0 | 0 | 0 | 0 | (0.74, 0.74) | (0.98, 0.98) | (0.50, 0.51) | ||
| 5 | −1.4 | 1 | 0 | 0 | 0 | 0 | (0.21, 0.21) | (0.34, 0.33) | (0.08, 0.08) | ||
| 6 | −0.5 | 1 | 0 | 0 | 0 | 0 | (0.50, 0.51) | (0.70, 0.70) | (0.30, 0.31) | ||
| 7 | 0 | 0 | 0 | 0.5 | 0 | 0 | (0.70, 0.50) | (0.70, 0.50) | (0.70, 0.51) | ||
| 8 | −0.5 | 0.3 | 0 | 0.5 | 0 | 0 | (0.56, 0.36) | (0.62, 0.41) | (0.50, 0.31) | ||
| 9 | −0.5 | 1 | 0 | 0.5 | 0 | 0 | (0.70, 0.51) | (0.85, 0.70) | (0.50, 0.31) | ||
| 10 | 0 | 0 | 0 | 0.5 | 0.2 | 0 | (0.73, 0.50) | (0.76, 0.49) | (0.70, 0.51) | ||
| 11 | −0.5 | 1 | 0 | 0.5 | 0.2 | 0 | (0.70, 0.51) | (0.88, 0.70) | (0.50, 0.31) | ||
| Patients with x1=x2=1 | Patients without x1=x2=1 | ||||||||||
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | (0.50, 0.50) | (0.50, 0.50) | (0.50, 0.50) | ||
| 13 | −1 | 0.5 | 0.2 | 0 | 0 | 0 | (0.30, 0.30) | (0.38, 0.38) | (0.23, 0.22) | ||
| 14 | −1 | 0.5 | 0.8 | 0 | 0 | 0 | (0.46, 0.46) | (0.62, 0.62) | (0.29, 0.29) | ||
| 15 | −1 | 1.5 | 0.8 | 0 | 0 | 0 | (0.66, 0.66) | (0.90, 0.90) | (0.42, 0.42) | ||
| 16 | 0 | 0 | 0 | 0.5 | 0 | 0 | (0.69, 0.50) | (0.69, 0.50) | (0.69, 0.49) | ||
| 17 | −1 | 0.5 | 0.8 | 0.5 | 0 | 0 | (0.63, 0.46) | (0.79, 0.62) | (0.48, 0.29) | ||
| 18 | −1 | 0.5 | 0.8 | 0.5 | 0.2 | 0.3 | (0.72, 0.46) | (0.90, 0.62) | (0.54, 0.29) | ||
| 19 | −2 | 0.5 | 0.8 | 0.5 | 0.2 | 0.3 | (0.41, 0.16) | (0.62, 0.24) | (0.20, 0.07) | ||
| 20 | −2 | 0.5 | 0.8 | 0.5 | 0.5 | 0.8 | (0.58, 0.16) | (0.86, 0.24) | (0.30, 0.07) | ||
We considered six randomization methods for the clinical trial design: traditional fixed 1:1 randomization (Trad), response-adaptive randomization without incorporating biomarkers (RAR), and response-adaptive randomization incorporating biomarkers (i.e., biomarker-driven randomization) CARA1-CARA4. Note that RAR and CARA1-CARA4 requires the calculation of the allocation ratio based on data and use the fixed 1:1 ratio to randomize the patients in the first cohort and update the allocation ratio sequentially to enroll and randomize the patients for the next cohort. For all designs (Trad, RAR, CARA1-CARA4), we assumed a maximum sample size of 210 and performed in a group sequential manner we described in the previous section. They include two interim analyses at 70 and 140 patients with a final analysis when the last patient was enrolled and finished the outcome evaluation (i.e., K=3). The analysis time points were chosen by equal increments of information. We set the overall type I error rate to 0.05, and the O’Brien-Fleming alpha spending function (44) is used to specify the stopping boundaries for sequential tests. At interims, we monitored the superiority and futility of treatment A against B, which allows the early stopping of the trial. At the final analysis, we made a conclusion that A is superior to B or not. A chi-square test was used to analyze the outcome at interims and final analysis.
We fit the Bayesian probit regression model assuming normal priors with zero mean vector and diagonal covariance matrix with diagonal elements 108, 102, and 0.5. The large diagonal elements of the prior covariance matrix indicate vague prior while the small diagonal element such as 0.5 indicates informative prior. We ran the algorithm under R version 4.1.2 using the package LearnBayes version 2.15.1 for 10,000 iterations and discarded the first 5,000 iterations as burn-in. The source code is provided in Appendix 1. We considered the following measures to examine the performance of the designs:
- The rejection probability is the percentage of rejections of the null hypothesis supporting no difference of the response rate between two arms A and B based on 1,000 simulated trials. The rejection probability under scenarios 1–6 and 12–15 indicate the estimated type I error rate, and the rejection probability under scenarios 7–11 and 16–20 indicates the power.
- The estimated effect size is the difference of the response proportion between A and B at the final analysis based on 1,000 simulated trials.
- Early stopping probability is the proportion of the early stopping due to superiority or futility based on 1,000 simulated trials.
- The average difference of the number of patients allocated to A and B across 1,000 simulated trials.
- The average number of failures across 1,000 simulated trials.
The estimated rejection probability presented in Table 2 under the null scenarios, i.e., scenarios 1–6 and 12–15, indicates the overall type I error rate. Both Trad and RAR designs preserved the overall type I error rate at the target level for all null scenarios no matter what biomarker profiles are. All CARA1-CARA4 designs also preserved the overall type I error rate when both biomarkers and treatments have no effect on the response, i.e., scenarios 1 and 12. However, CARA1-CARA4 designs were influenced by the informative biomarkers under the null scenarios where there is no patient who gets benefit from A against B, i.e., there is no treatment effect. We found serious error inflations due to the biomarker-driven randomization when there exists an effect of informative biomarkers. Using vague prior distribution, the overall type I error rates under scenarios 2–6 and 13–15 were 0.17, 0.06, 0.18, and 0.11 on average for CARA1-CARA4 designs, respectively. Using informative prior distribution, they were 0.11, 0.05, 0.11, 0.08 on average for CARA1-CARA4 designs, respectively. We found that the performance of the group sequential design using the biomarker-driven randomization is sensitive to the prior choice, and informative prior helps to avoid huge inflation of the overall type I error rate. Specifically, under CARA2 design, in scenarios 5 and 15 the estimated type I error rates were inflated at 10–15% when the uninformative normal prior was used while it seems controlled at 5% when the informative normal prior was used. In addition, regardless of the prior distribution, CARA4 design led to less inflation of the type I error rate compared to CARA1 and CARA3.
Table 2
| Sc. | (PA,PB) | Trad | RAR | CARA1 | CARA2 | CARA3 | CARA4 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Prr 1 | Prr 2 | Prr 3 | Prr 1 | Prr 2 | Prr 3 | Prr 1 | Prr 2 | Prr 3 | Prr 1 | Prr 2 | Prr 3 | |||||||
| 1 | (0.50, 0.50) | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.06 | 0.06 | 0.06 | 0.04 | 0.04 | 0.04 | 0.05 | 0.05 | 0.05 | |||
| 2 | (0.56, 0.57) | 0.05 | 0.05 | 0.06 | 0.06 | 0.06 | 0.05 | 0.05 | 0.06 | 0.06 | 0.06 | 0.04 | 0.06 | 0.06 | 0.06 | |||
| 3 | (0.70, 0.70) | 0.05 | 0.05 | 0.11 | 0.11 | 0.08 | 0.04 | 0.04 | 0.05 | 0.19 | 0.18 | 0.10 | 0.10 | 0.14 | 0.08 | |||
| 4 | (0.74, 0.74) | 0.05 | 0.05 | 0.38 | 0.27 | 0.13 | 0.03 | 0.03 | 0.04 | 0.25 | 0.32 | 0.26 | 0.17 | 0.29 | 0.14 | |||
| 5 | (0.21, 0.21) | 0.05 | 0.05 | 0.18 | 0.14 | 0.11 | 0.14 | 0.16 | 0.06 | 0.21 | 0.21 | 0.09 | 0.13 | 0.13 | 0.06 | |||
| 6 | (0.50, 0.51) | 0.05 | 0.05 | 0.15 | 0.15 | 0.10 | 0.03 | 0.03 | 0.05 | 0.13 | 0.13 | 0.09 | 0.09 | 0.08 | 0.07 | |||
| 7 | (0.70, 0.50) | 0.80 | 0.79 | 0.77 | 0.78 | 0.78 | 0.80 | 0.80 | 0.78 | 0.76 | 0.79 | 0.79 | 0.80 | 0.80 | 0.79 | |||
| 8 | (0.56, 0.36) | 0.81 | 0.77 | 0.74 | 0.74 | 0.78 | 0.80 | 0.80 | 0.81 | 0.79 | 0.79 | 0.80 | 0.82 | 0.83 | 0.80 | |||
| 9 | (0.70, 0.51) | 0.70 | 0.68 | 0.62 | 0.63 | 0.75 | 0.66 | 0.66 | 0.70 | 0.68 | 0.66 | 0.77 | 0.78 | 0.77 | 0.76 | |||
| 10 | (0.73, 0.50) | 0.91 | 0.91 | 0.90 | 0.90 | 0.89 | 0.91 | 0.91 | 0.90 | 0.90 | 0.90 | 0.89 | 0.91 | 0.91 | 0.91 | |||
| 11 | (0.70, 0.51) | 0.80 | 0.81 | 0.79 | 0.81 | 0.88 | 0.77 | 0.76 | 0.81 | 0.82 | 0.81 | 0.89 | 0.88 | 0.90 | 0.88 | |||
| 12 | (0.50, 0.50) | 0.04 | 0.04 | 0.05 | 0.05 | 0.06 | 0.06 | 0.06 | 0.06 | 0.04 | 0.04 | 0.04 | 0.05 | 0.05 | 0.05 | |||
| 13 | (0.30, 0.30) | 0.06 | 0.06 | 0.07 | 0.08 | 0.08 | 0.06 | 0.06 | 0.06 | 0.04 | 0.04 | 0.04 | 0.05 | 0.05 | 0.05 | |||
| 14 | (0.46, 0.46) | 0.04 | 0.06 | 0.07 | 0.08 | 0.08 | 0.06 | 0.06 | 0.05 | 0.08 | 0.08 | 0.07 | 0.07 | 0.07 | 0.07 | |||
| 15 | (0.66, 0.66) | 0.05 | 0.05 | 0.28 | 0.26 | 0.20 | 0.09 | 0.09 | 0.04 | 0.35 | 0.37 | 0.18 | 0.16 | 0.15 | 0.11 | |||
| 16 | (0.69, 0.50) | 0.80 | 0.79 | 0.78 | 0.78 | 0.77 | 0.80 | 0.80 | 0.78 | 0.76 | 0.79 | 0.79 | 0.80 | 0.80 | 0.79 | |||
| 17 | (0.63, 0.46) | 0.75 | 0.70 | 0.64 | 0.67 | 0.80 | 0.66 | 0.66 | 0.71 | 0.65 | 0.64 | 0.79 | 0.75 | 0.76 | 0.75 | |||
| 18 | (0.72, 0.46) | 0.96 | 0.95 | 0.94 | 0.95 | 0.98 | 0.95 | 0.92 | 0.97 | 0.93 | 0.94 | 0.99 | 0.98 | 0.97 | 0.97 | |||
| 19 | (0.41, 0.16) | 0.96 | 0.92 | 0.85 | 0.91 | 0.96 | 0.83 | 0.80 | 0.96 | 0.84 | 0.81 | 0.98 | 0.95 | 0.93 | 0.93 | |||
| 20 | (0.58, 0.16) | 1.00 | 1.00 | 0.99 | 1.00 | 1.00 | 1.00 | 0.98 | 1.00 | 0.92 | 0.98 | 1.00 | 1.00 | 1.00 | 1.00 | |||
RAR, response-adaptive randomization; CARA, covariate-adjusted RAR.
The estimated rejection probability under the alternative scenarios, i.e., scenarios 7–11 and 16–20, indicates the power. Trad design yielded power 0.8 in scenarios 7, 8, 11, and 16, 0.7 in scenarios 9, 0.75 in scenario 17, 0.91 in scenario 10, 0.96 in scenarios 18 and 19, and 1 in scenario 20. The smaller or larger overall treatment effect difference (i.e., PA−PB) made the power different in scenarios. RAR design showed a little smaller power than Trad design in most cases. Using the biomarker-driven randomization, we observed that the estimated type II error rate could be inflated when uninformative prior was used, implying that CARA1-CARA4 designs could be less powerful than Trad and RAR designs. However, CARA1 CARA4 designs yielded similar or larger power compared to Trad and RAR designs when informative prior was used. From the simulation results in Table 2, it is recommended to consider informative prior rather than vague prior in the biomarker-driven randomization to minimize both type I and II error rates. Therefore, we used the informative prior in the remaining to compare the performance of the designs.
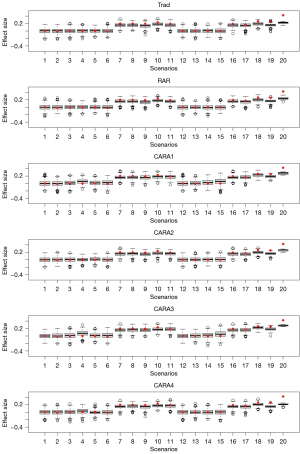
Figure 3 shows the estimated effect size at the final analysis computed as the difference of the response proportion between A and B at the final analysis. Trad, RAR, and CARA2 designs showed a similar pattern across the scenarios. Under the null scenarios (i.e., scenarios 1–6 and 12–15), they showed that the average of the estimated effect size at the final analysis is almost the same as the true effect size. Under the alternative scenarios (i.e., scenarios 7–11 and 16–20), they showed that the average of the estimated effect size is smaller than the true effect size. CARA1, CARA3, and CARA4 designs yielded a larger estimated effect size than the true effect size in some null scenarios in Figure 3. This explains the type I error rate inflation in Table 2. Specifically, CARA1 design led to more than 10% overall type I error rate in scenarios 4, 5, 6, 14, and 15, CARA3 design led to overall type I error rates 26% and 18% in scenarios 4 and 15, respectively, and CARA4 design led to overall type I error rate14% in scenario 4. Under the alternative scenarios, CARA1, CARA3, and CARA4 designs showed a similar pattern to Trad, RAR, and CARA2 designs.
As seen in Table 2 and Figure 3, CARA1, CARA3, and CARA4 designs yielded larger inflation of the type I error rate in scenario 4. We further investigated the distribution of biomarker status in each treatment arm under scenario 4. The results are given in Figure 4. Trad, RAR, and CARA2 designs showed the almost same proportion between treatment arm A and B of subgroups classified by the status of the biomarker x1. For example, Trad design showed that 48.2% of patients with x1=1 received treatment arm A and 48.1% of patients with x1=1 received treatment B. However, CARA1, CARA3, and CARA4 designs showed an unbalanced allocation ratio for each subgroup. CARA1 design showed that 55.2% of patients with x1=1 received treatment arm A and 44.3% of patients with x1=1 received the treatment B. CARA3 design showed that 55.8% of patients with x1=1 received treatment arm A and 41.8% of patients with x1=1 received the treatment B. CARA4 design showed that 52.9% of patients with x1=1 received treatment arm A and 46.1% of patients with x1=1 received the treatment B. Since biomarkers have an influence on the response directly or indirectly, the distribution of the biomarker status affects the outcomes of the clinical trials.
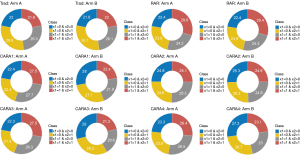
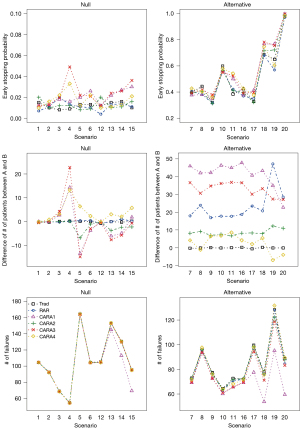
Figure 5 shows early stopping probability, the difference of the number of patients allocated to A and B, and the number of failures. For each null scenario, early stopping probability was not different across designs except scenarios 4 and 15, where CARA1, CARA3, and CARA4 designs showed a larger difference compared to the Trad, RAR, and CARA2 designs. As noted above, in scenarios 4 and 15, CARA1, CARA3, and CARA4 designs were more stopped early from the wrong decision and led to inflation of the estimated type I error rate. In addition, early stopping probability was similar across designs in alternative scenarios except scenarios 11, 17–19. CARA1, CARA3, and CARA4 designs showed a larger early stopping probability in scenarios 11 and 17 resulting in a larger power compared to Trad, RAR, and CARA2 designs. The difference of the number of patients allocated to A and B and the number of failures are interesting to be investigated under the alternative scenarios (see the right panels of Figure 5). RAR and CARA1-CARA4 designs change the randomization ratio adaptively based on accumulating data so that more patients are likely to get better performing treatment. In most alternative scenarios, i.e., 7–11 and 16–20, we observed that a larger number of patients were assigned to the superior treatment A under RAR and CARA1-CARA4 designs. Compared to RAR design, CARA1 and CARA3 designs showed superior performance in the difference of the number of patients assigned to treatment between A and B while CARA2 and CARA4 designs performed worse. Moreover, CARA1-CARA4 designs led to a smaller number of failures than Trad and RAR designs, which implies that CARA1-CARA4 designs showed better improvement in patients’ clinical benefit. As the heterogeneity increases and the proportion of the treatment-sensitive subgroup is smaller than the insensitive subgroup, i.e., under scenarios 17–20, CARA1 design showed superior performance in terms of the number of failures in our simulation study. CARA2 and CARA4 designs resulted in more failures than CARA1 and CARA3 designs, but CARA2 and CARA4 designs were not worse than Trad and RAR designs.
We also investigated the performance and compared the designs when the prevalence rate of the first biomarker varies. The results are provided in Tables 3,4. The estimated type I error rate was 0.09, 0.04, 0.09, and 0.06 on average for CARA1-CARA4 designs, respectively, when the proportion of having the first marker positive is 0.7; it was 0.10, 0.05, 0.10, and 0.07 when the proportion of having the first marker positive is 0.5; and it was 0.08, 0.05, 0.09, and 0.07 when the proportion of having the first marker positive is 0.25. We still observed the type I error inflation using the biomarker-driven randomization with the lower or higher prevalence rate, because x1 is a prognostic biomarker in most null scenarios. The power was 0.87, 0.86, 0.88, 0.87 on average for CARA1-CARA4 designs, respectively, when the proportion of having the first marker positive is 0.7; it was 0.86, 0.85, 0.87, and 0.86 when the proportion of having the first marker positive is 0.5; and it was 0.84, 0.84, 0.86, and 0.85 when the proportion of having the first marker positive is 0.25. Since the first biomarker has a predictive effect on the response, the power shrunk for all CARA1-CARA4 designs as the prevalence rate of the biomarker x1 is lower. We also summarized in the following the measures of the clinical benefit under the alternative scenarios as the prevalence rate of x1 varies. When the proportion of having the first marker positive is 0.7, the difference of the number of patients allocated to A and B was 42.2, 8.1, 33.7, and 3.5 on average for CARA1-CARA4 designs, respectively; when the proportion of having the first marker positive is 0.5, it was 41.2, 8.7, 33.0, and 2.6; and when the proportion of having the first marker positive is 0.25, it was 41.4, 8.9, 32.3, and 0.7. CARA4 design showed that the difference of the number of patients allocated to A and B decreases as the prevalence rate of the biomarker decreases while CARA1-CARA3 designs did not change much the difference of the number of patients in the prevalence rate. The number of failures was 72.5, 77.0, 73.3, and 77.0 on average for CARA1-CARA4 designs, respectively, when the proportion of having the first marker positive is 0.7; it was 71.8, 83.9, 80.0, and 84.5 when the proportion of having the first marker positive is 0.5; and it was 88.5, 92.8, 89.1, and 93.6 when the proportion of having the first marker positive is 0.25. Thus, CARA1-CARA4 designs showed the improved clinical benefit (i.e., the number of the failures decreases) as the prevalence rate of the biomarker x1 increases.
Table 3
| Sc. | (PA,PB) | Trad | RAR | CARA1 | CARA2 | CARA3 | CARA4 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RejP | DiffA | NF | RejP | DiffA | NF | RejP | DiffA | NF | RejP | DiffA | NF | |||||||
| 1 | (0.50, 0.50) | 0.06 | 0.05 | 0.06 | 1.9 | 104.7 | 0.05 | 1.0 | 105.1 | 0.05 | −0.5 | 104.8 | 0.03 | −0.2 | 105.3 | |||
| 2 | (0.56, 0.57) | 0.06 | 0.04 | 0.07 | 1.8 | 86.8 | 0.06 | 0.4 | 86.9 | 0.06 | 2.1 | 87.1 | 0.05 | 1.2 | 887.6 | |||
| 3 | (0.70, 0.70) | 0.06 | 0.05 | 0.08 | 5.6 | 54.5 | 0.04 | 0.3 | 54.6 | 0.10 | 6.9 | 54.5 | 0.07 | 3.9 | 54.7 | |||
| 4 | (0.74, 0.74) | 0.05 | 0.05 | 0.16 | 22.1 | 34.6 | 0.04 | 0.3 | 35.0 | 0.29 | 30.9 | 34.2 | 0.16 | 18.6 | 34.3 | |||
| 5 | (0.21, 0.21) | 0.05 | 0.05 | 0.09 | −8.3 | 153.8 | 0.04 | −4.9 | 153.7 | 0.06 | −9.7 | 153.9 | 0.06 | 5.2 | 153.4 | |||
| 6 | (0.50, 0.51) | 0.04 | 0.07 | 0.11 | −2.5 | 88.0 | 0.04 | 0.5 | 88.4 | 0.09 | −2.3 | 87.8 | 0.06 | 2.2 | 88.7 | |||
| 7 | (0.70, 0.50) | 0.78 | 0.79 | 0.76 | 46.4 | 69.2 | 0.82 | 7.4 | 72.0 | 0.80 | 34.6 | 69.4 | 0.81 | 4.3 | 72.0 | |||
| 8 | (0.56, 0.36) | 0.82 | 0.79 | 0.79 | 43.8 | 89.1 | 0.80 | 8.5 | 91.0 | 0.79 | 32.4 | 90.4 | 0.81 | −1.1 | 90.8 | |||
| 9 | (0.70, 0.51) | 0.67 | 0.70 | 0.78 | 43.6 | 59.1 | 0.68 | 6.1 | 63.4 | 0.76 | 36.5 | 59.7 | 0.75 | 10.4 | 61.1 | |||
| 10 | (0.73, 0.50) | 0.95 | 0.95 | 0.92 | 48.3 | 57.5 | 0.94 | 6.9 | 60.4 | 0.94 | 37.2 | 57.7 | 0.95 | 5.8 | 60.6 | |||
| 11 | (0.70, 0.51) | 0.86 | 0.83 | 0.92 | 47.8 | 51.0 | 0.83 | 6.5 | 57.3 | 0.91 | 41.1 | 51.8 | 0.89 | 13.0 | 54.9 | |||
| 12 | (0.50, 0.50) | 0.04 | 0.04 | 0.06 | 1.9 | 104.7 | 0.05 | 1.0 | 105.1 | 0.05 | −0.5 | 104.8 | 0.03 | −0.2 | 105.3 | |||
| 13 | (0.30, 0.30) | 0.05 | 0.06 | 0.06 | −6.4 | 146.9 | 0.05 | −2.3 | 147.2 | 0.06 | −6.2 | 147.3 | 0.04 | 2.7 | 147.0 | |||
| 14 | (0.46, 0.46) | 0.06 | 0.05 | 0.10 | −5.6 | 123.4 | 0.05 | −2.0 | 123.4 | 0.08 | −3.9 | 123.4 | 0.06 | 2.7 | 123.5 | |||
| 15 | (0.66, 0.66) | 0.07 | 0.05 | 0.16 | 1.0 | 73.9 | 0.05 | −0.7 | 74.0 | 0.16 | 2.1 | 73.9 | 0.10 | 5.9 | 73.5 | |||
| 16 | (0.69, 0.50) | 0.80 | 0.79 | 0.76 | 46.4 | 69.2 | 0.82 | 7.4 | 72.0 | 0.80 | 34.6 | 69.4 | 0.81 | 4.3 | 72.0 | |||
| 17 | (0.63, 0.46) | 0.71 | 0.71 | 0.79 | 40.2 | 86.1 | 0.74 | 7.2 | 92.9 | 0.82 | 30.2 | 87.7 | 0.77 | 2.4 | 91.4 | |||
| 18 | (0.72, 0.46) | 0.97 | 0.95 | 0.99 | 43.0 | 63.2 | 0.98 | 8.3 | 68.4 | 0.99 | 36.5 | 63.8 | 0.98 | 6.2 | 68.5 | |||
| 19 | (0.41, 0.16) | 0.98 | 0.96 | 0.99 | 33.3 | 107.2 | 0.98 | 13.0 | 115.4 | 0.99 | 28.4 | 109.0 | 0.97 | −7.8 | 119.0 | |||
| 20 | (0.58, 0.16) | 1.00 | 1.00 | 1.00 | 29.1 | 73.0 | 1.00 | 9.2 | 77.4 | 1.00 | 25.5 | 73.7 | 1.00 | −2.9 | 80.0 | |||
RAR, response-adaptive randomization; CARA, covariate-adjusted RAR.
Table 4
| Sc. | (PA,PB) | Trad | RAR | CARA1 | CARA2 | CARA3 | CARA4 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RejP | DiffA | NF | RejP | DiffA | NF | RejP | DiffA | NF | RejP | DiffA | NF | |||||||
| 1 | (0.50, 0.50) | 0.06 | 0.05 | 0.05 | −1.0 | 105.0 | 0.06 | −0.1 | 104.7 | 0.05 | −0.5 | 104.8 | 0.06 | 1.4 | 104.2 | |||
| 2 | (0.56, 0.57) | 0.06 | 0.04 | 0.05 | −3.0 | 98.4 | 0.05 | 0.3 | 98.2 | 0.06 | 0.4 | 98.5 | 0.06 | 0.6 | 98.8 | |||
| 3 | (0.70, 0.70) | 0.06 | 0.05 | 0.06 | 1.8 | 86.7 | 0.05 | 0.7 | 86.4 | 0.09 | 3.6 | 86.1 | 0.06 | 2.5 | 86.6 | |||
| 4 | (0.74, 0.74) | 0.05 | 0.05 | 0.08 | 5.9 | 79.7 | 0.04 | 0.4 | 79.8 | 0.14 | 12.7 | 79.5 | 0.09 | 7.9 | 79.4 | |||
| 5 | (0.21, 0.21) | 0.05 | 0.05 | 0.10 | −17.7 | 178.3 | 0.05 | −9.4 | 178.8 | 0.09 | −7.5 | 177.9 | 0.06 | 9.1 | 178.0 | |||
| 6 | (0.50, 0.51) | 0.04 | 0.07 | 0.07 | −4.2 | 124.1 | 0.04 | −2.7 | 124.2 | 0.09 | −2.4 | 123.9 | 0.07 | 2.2 | 124.1 | |||
| 7 | (0.70, 0.50) | 0.78 | 0.79 | 0.78 | 46.7 | 68.1 | 0.81 | 7.5 | 72.7 | 0.79 | 35.3 | 70.2 | 0.81 | 5.1 | 72.7 | |||
| 8 | (0.56, 0.36) | 0.82 | 0.79 | 0.77 | 43.3 | 99.5 | 0.82 | 10.0 | 101.2 | 0.79 | 32.2 | 100.4 | 0.79 | −2.4 | 102.4 | |||
| 9 | (0.70, 0.51) | 0.67 | 0.70 | 0.71 | 45.4 | 91.0 | 0.71 | 8.8 | 94.3 | 0.77 | 33.9 | 90.3 | 0.79 | 2.5 | 90.8 | |||
| 10 | (0.73, 0.50) | 0.95 | 0.95 | 0.82 | 46.7 | 65.3 | 0.87 | 6.8 | 67.0 | 0.85 | 35.9 | 65.6 | 0.85 | 4.7 | 68.4 | |||
| 11 | (0.70, 0.51) | 0.86 | 0.83 | 0.83 | 46.1 | 85.5 | 0.79 | 8.2 | 90.2 | 0.86 | 33.9 | 84.7 | 0.86 | 2.9 | 86.9 | |||
| 12 | (0.50, 0.50) | 0.04 | 0.04 | 0.06 | −1.0 | 105.0 | 0.06 | −0.1 | 104.7 | 0.05 | −0.5 | 104.8 | 0.06 | 1.4 | 104.2 | |||
| 13 | (0.30, 0.30) | 0.05 | 0.06 | 0.05 | −11.2 | 162.0 | 0.05 | −4.1 | 162.2 | 0.07 | −9.3 | 162.1 | 0.05 | 3.2 | 162.3 | |||
| 14 | (0.46, 0.46) | 0.06 | 0.05 | 0.11 | −9.0 | 139.1 | 0.04 | −4.0 | 139.3 | 0.08 | −7.6 | 138.7 | 0.06 | 3.4 | 139.4 | |||
| 15 | (0.66, 0.66) | 0.07 | 0.05 | 0.16 | −7.8 | 120.8 | 0.03 | −3.8 | 122.4 | 0.16 | −4.2 | 120.6 | 0.10 | 4.8 | 121.5 | |||
| 16 | (0.69, 0.50) | 0.80 | 0.79 | 0.78 | 46.7 | 68.1 | 0.81 | 7.5 | 72.7 | 0.79 | 35.3 | 70.2 | 0.81 | 5.1 | 72.7 | |||
| 17 | (0.63, 0.46) | 0.71 | 0.71 | 0.79 | 40.7 | 102.6 | 0.73 | 8.5 | 105.8 | 0.79 | 30.3 | 102.0 | 0.76 | 0.2 | 106.7 | |||
| 18 | (0.72, 0.46) | 0.97 | 0.95 | 0.98 | 41.2 | 80.6 | 0.93 | 9.0 | 87.4 | 0.98 | 32.0 | 80.1 | 0.95 | 2.9 | 87.0 | |||
| 19 | (0.41, 0.16) | 0.98 | 0.96 | 0.96 | 27.9 | 129.7 | 0.93 | 11.8 | 136.7 | 0.96 | 26.1 | 131.0 | 0.86 | −8.6 | 145.4 | |||
| 20 | (0.58, 0.16) | 1.00 | 1.00 | 1.00 | 29.5 | 94.6 | 1.00 | 11.0 | 99.6 | 1.00 | 27.5 | 96.4 | 1.00 | −5.9 | 103.0 | |||
Our simulation study provides several interesting results and challenges in the biomarker-driven randomization. First, all designs preserved the overall type I error rate at the target level under the null scenarios which have no any effect of informative biomarkers and treatment on the response. Trad and RAR designs did not use biomarkers and preserved the estimated type I error rate no matter what the biomarker profiles of patients are while CARA1-CARA4 designs using biomarkers for adaptive randomization could lead to inflation depending on the effect of the informative biomarkers. We brought up the error inflation problem and showed the impact of the commonly used adaptive allocation methods incorporating biomarkers in the context of group sequential trials. Secondly, we observed in Table 2 that CARA1-CARA4 designs resulted in the type I error inflation when we used vague prior distribution to fit the Bayesian probit regression model for the allocation probability. Using the informative prior led to smaller inflation of the estimated type I error rate. Therefore, considering the informative prior in the estimation of the response probability to update the allocation probability would help to minimize the error rates. Moreover, there are more opportunities to borrow information from previous trials and knowledge to specify the prior distribution. Third, as seen in Table 2 and Figure 5, there is a trade-off between statistical conservativeness (i.e., controlling error rates and attaining reasonable power) and clinical improvement (e.g., ethic and clinical benefits). CARA2 design using informative prior preserved the overall error rates but didn’t provide more clinical gain compared to RAR design, which does not incorporate the biomarkers, i.e., it was less ethical and yielded more failures. Thus, we couldn’t get benefit from using the biomarkers under the CARA2 design using informative prior. CARA1 and CARA3 designs using informative prior were more ethical and improved the clinical benefit compared to RAR design, but they still suffered from the type I error rate inflation. CARA4 design using informative prior led to type I error inflation in some scenarios and didn’t provide clinical gain compared to RAR and CARA2 designs.
Discussion
We have investigated the biomarker-driven randomization in two-arm group sequential trials. We considered several types of biomarker-driven randomization, which are the covariate-adjusted version of the existing response-adaptive randomization, and discussed the performance in terms of the type I/II error rates, the estimated effect size at the final analysis, early stopping probability, the difference of the number of patients allocated to two treatments, and the number of failures. A variety of scenarios were considered to see the impact due to incorporating biomarkers in adaptive randomization and learn the lessons from the simulation study.
When there is no any effect of biomarkers or the treatment on the response, the biomarker-driven randomization preserved the overall type I error rate. However, if prognostic biomarkers exist in null scenarios, our study showed the type I error rate inflation with the vague prior. Using the informative prior, the inflation shrunk for all methods we considered and even some methods (e.g., CARA2) preserved the type I error rate. However, the estimated type I error rates were still likely to be inflated under CARA1, CARA3, and CARA4 designs even when the informative prior was considered. The inflation of the overall type I error rate got worse seriously with the strong signal. Specifically, the error inflations were observed when there is an effect of prognostic biomarkers, which has a larger difference in response P than 0.1.
One of possible suggestions to control type I error rate is to use simulations to calibrate the appropriate critical values for group sequential testing based on the skewed patients to the favorable treatment due to the biomarker-driven randomization (45). We propose the cutoff calibration based on preliminary simulations to control type I error rate as follows:
- Step 1: Specify the null scenarios with certain response probabilities for the preliminary simulations, i.e., scenarios 1–6 and 12–15 in Table 1.
- Step 2: Elicit the fine grid of
, for i=1,...,M, with
. Start with the desirable type I error rate α to determine the critical values at each analysis using an error spending function.
- Step 3: Given the critical values in Step 2, run the preliminary simulations for all prespecified null scenarios and obtain the estimated type I error rates.
- Step 4: If the estimated type I error rates obtained from the preliminary simulations are less than or equal to the α, we obtain the evidence that the type I error rate is adequately controlled and the identified critical values are ready to use for the sequential test and adaptive design. Otherwise, we replace
with the next candidate
, which is the maximum of values being smaller than
, to repeat Step 3-4 until the estimated type I error rates are less than or equal to the target level of α.
Following the above procedure, we investigated the operating characteristics of the group sequential designs using CARA1, CARA3, and CARA4 designs. The results are presented in Tables 5,6, assuming the normal priors with zero mean vector and diagonal covariance matrix with diagonal elements 0.5 to fit the Bayesian probit regression model. Depending on situations (i.e., the difference of null response probability P between subgroups resulted from the effect of prognostic biomarkers), stringent cutoffs were identified to control the type I error rate, and we lost the power to detect the difference between treatment groups, i.e., the estimated type II error rate was inflated. Moreover, with the calibrated cutoff, the clinical benefit disappeared but designs were still ethical compared to RAR design. It seems unfair to calibrate the cutoffs preserving the type I error rate for all possible effects of prognostic biomarkers, because the design unnecessarily sacrifices the power. Rather, we need to study the maximum allowable difference between subgroups influenced by the prognostic biomarkers for the cutoff calibration.
Table 5
| Sc. | (PA,PB) | Trad | RAR | CARA1 | CARA2 | CARA3 | CARA4 |
|---|---|---|---|---|---|---|---|
| Estimated rejection probability (i.e., overall type I error rate) | |||||||
| 1 | (0.50, 0.50) | 0.05 | 0.05 | 0.02 | 0.06 | 0.00 | 0.01 |
| 2 | (0.56, 0.57) | 0.05 | 0.46 | 0.02 | 0.06 | 0.00 | 0.01 |
| 3 | (0.70, 0.70) | 0.05 | 0.05 | 0.02 | 0.05 | 0.01 | 0.02 |
| 4 | (0.74, 0.74) | 0.05 | 0.05 | 0.05 | 0.04 | 0.05 | 0.05 |
| 5 | (0.21, 0.21) | 0.05 | 0.05 | 0.05 | 0.06 | 0.01 | 0.01 |
| 6 | (0.50, 0.51) | 0.05 | 0.05 | 0.03 | 0.05 | 0.01 | 0.01 |
| Estimated rejection probability (i.e., power) | |||||||
| 7 | (0.70, 0.50) | 0.80 | 0.79 | 0.56 | 0.78 | 0.34 | 0.56 |
| 8 | (0.56, 0.36) | 0.81 | 0.77 | 0.57 | 0.81 | 0.37 | 0.56 |
| 9 | (0.70, 0.51) | 0.70 | 0.68 | 0.59 | 0.70 | 0.40 | 0.51 |
| 10 | (0.73, 0.50) | 0.91 | 0.91 | 0.72 | 0.90 | 0.55 | 0.73 |
| 11 | (0.70, 0.51) | 0.80 | 0.81 | 0.75 | 0.81 | 0.57 | 0.70 |
| Difference of the number of patients between A and B denoted by nA−nB | |||||||
| 7 | (0.70, 0.50) | −0.2 | 18.0 | 58.4 | 8.2 | 45.9 | 6.2 |
| 8 | (0.56, 0.36) | −0.2 | 24.0 | 53.3 | 9.2 | 45.0 | 1.1 |
| 9 | (0.70, 0.51) | 0.1 | 16.9 | 53.9 | 7.0 | 47.6 | 8.1 |
| 10 | (0.73, 0.50) | −0.1 | 17.8 | 61.3 | 7.6 | 54.2 | 8.0 |
| 11 | (0.70, 0.51) | 0.1 | 17.7 | 56.4 | 6.8 | 53.6 | 11.3 |
| Number of failures | |||||||
| 7 | (0.70, 0.50) | 73.0 | 71.2 | 74.8 | 72.5 | 79.4 | 80.8 |
| 8 | (0.56, 0.36) | 96.2 | 95.3 | 102.2 | 96.2 | 107.6 | 108.2 |
| 9 | (0.70, 0.51) | 77.5 | 76.4 | 78.1 | 76.6 | 81.3 | 82.7 |
| 10 | (0.73, 0.50) | 64.6 | 63.1 | 67.0 | 63.9 | 72.6 | 73.8 |
| 11 | (0.70, 0.51) | 72.8 | 70.9 | 71.5 | 71.9 | 77.3 | 77.6 |
RAR, response-adaptive randomization; CARA, covariate-adjusted RAR.
Table 6
| Sc. | (PA,PB) | Trad | RAR | CARA1 | CARA2 | CARA3 | CARA4 |
|---|---|---|---|---|---|---|---|
| Estimated rejection probability (i.e., overall type I error rate) | |||||||
| 12 | (0.50, 0.50) | 0.05 | 0.05 | 0.00 | 0.06 | 0.01 | 0.02 |
| 13 | (0.30, 0.30) | 0.04 | 0.05 | 0.01 | 0.05 | 0.01 | 0.01 |
| 14 | (0.46, 0.46) | 0.05 | 0.05 | 0.03 | 0.03 | 0.03 | 0.02 |
| 15 | (0.66, 0.66) | 0.05 | 0.05 | 0.05 | 0.04 | 0.05 | 0.06 |
| Estimated rejection probability (i.e., power) | |||||||
| 16 | (0.69, 0.50) | 0.80 | 0.80 | 0.46 | 0.78 | 0.56 | 0.66 |
| 17 | (0.63, 0.46) | 0.71 | 0.70 | 0.57 | 0.71 | 0.56 | 0.64 |
| 18 | (0.72, 0.46) | 0.97 | 0.97 | 0.91 | 0.97 | 0.92 | 0.94 |
| 19 | (0.41, 0.16) | 0.97 | 0.98 | 0.89 | 0.96 | 0.91 | 0.85 |
| 20 | (0.58, 0.16) | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Difference of the number of patients between A and B denoted by nA−nB | |||||||
| 16 | (0.69, 0.50) | −0.2 | 17.8 | 60.1 | 8.2 | 44.9 | 5.6 |
| 17 | (0.63, 0.46) | −0.0 | 20.1 | 52.8 | 8.3 | 38.8 | 0.9 |
| 18 | (0.72, 0.46) | −0.2 | 16.7 | 60.0 | 7.9 | 45.8 | 5.4 |
| 19 | (0.41, 0.16) | 0.6 | 57.7 | 48.8 | 12.3 | 39.6 | -10.4 |
| 20 | (0.58, 0.16) | 0.0 | 16.6 | 45.7 | 11.0 | 39.7 | -5.4 |
| Number of failures | |||||||
| 16 | (0.69, 0.50) | 72.8 | 71.0 | 76.3 | 72.5 | 77.1 | 78.7 |
| 17 | (0.63, 0.46) | 84.8 | 83.2 | 103.7 | 98.9 | 104.1 | 104.4 |
| 18 | (0.72, 0.46) | 63.1 | 60.9 | 82.8 | 76.7 | 82.2 | 84.1 |
| 19 | (0.41, 0.16) | 105.6 | 103.1 | 143.9 | 122.3 | 140.5 | 144.1 |
| 20 | (0.58, 0.16) | 65.7 | 62.2 | 95.7 | 87.8 | 94.7 | 102.4 |
RAR, response-adaptive randomization; CARA, covariate-adjusted RAR.
Before the clinical trial initiates, i.e., ideally when the protocol has developed for the trial, investigating the operating characteristics of the design has been recommended in practice. It means that we have a chance to see if the design preserves the overall type I error rate or not. If the type I error rate is not controlled at the nominal level, we recommend following the above procedure to calibrate the cutoff to use for the testing in the clinical trial. This will update stopping rules of the study at interims and final analysis.
It is also necessary to consider how to deal with the prognostic biomarkers. Prior to initiation of the clinical trials, knowledge of prognostic biomarkers will help to conduct stratified randomization and analyze the data along with the appropriate methods. However, if we have little information on prognostic biomarkers in the beginning, we need to check if there is an effect of prognostic biomarkers at interims. If there is a prognostic biomarker, the biomarker-driven randomization is likely to yield type I error inflation as we learned the lessons above. Thus, in order to minimize the errors, it is critical to consider the subgroups defined by the identified prognostic biomarkers and perform appropriately multiple testing based on the identified subgroups. Assuming that we do not have information on the prognostic biomarkers at the beginning of the trial, we checked if there is an effect of biomarkers at interims and used the information to tailor the stratified testing. We performed the stratified testing without multiplicity adjustment and with multiplicity adjustment. We provided the results in Tables 7,8. CARA1 and CARA3 designs still had at most 9% of the estimated type I error rate without multiplicity adjustment and preserved the error rate at 5% after the adjustment. However, we lost both power and clinical benefit from the multiplicity adjustment. CARA4 design without multiplicity adjustment showed that the type I error rate was controlled but its performance in terms of the ethic and clinical benefit was poor compared to RAR design. Thus, it was not necessary for CARA4 design to adjust the multiplicity, because it would unnecessarily sacrifice power after multiplicity adjustment.
Table 7
| Sc. | (PA,PB) | Trad | RAR | CARA1 | CARA2 | CARA3 | CARA4 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| No adj | Adj | No adj | Adj | No adj | Adj | ||||||
| Estimated rejection probability (i.e., overall type I error rate) | |||||||||||
| 1 | (0.50, 0.50) | 0.05 | 0.05 | 0.05 | 0.05 | 0.06 | 0.04 | 0.02 | 0.05 | 0.02 | |
| 2 | (0.56, 0.57) | 0.05 | 0.46 | 0.05 | 0.03 | 0.06 | 0.05 | 0.02 | 0.06 | 0.03 | |
| 3 | (0.70, 0.70) | 0.05 | 0.05 | 0.05 | 0.03 | 0.05 | 0.06 | 0.03 | 0.06 | 0.02 | |
| 4 | (0.74, 0.74) | 0.05 | 0.05 | 0.06 | 0.03 | 0.04 | 0.06 | 0.04 | 0.05 | 0.02 | |
| 5 | (0.21, 0.21) | 0.05 | 0.05 | 0.05 | 0.03 | 0.06 | 0.05 | 0.03 | 0.05 | 0.02 | |
| 6 | (0.50, 0.51) | 0.05 | 0.05 | 0.07 | 0.02 | 0.05 | 0.05 | 0.03 | 0.06 | 0.03 | |
| Estimated rejection probability (i.e., power) | |||||||||||
| 7 | (0.70, 0.50) | 0.80 | 0.79 | 0.78 | 0.78 | 0.78 | 0.74 | 0.66 | 0.78 | 0.65 | |
| 8 | (0.56, 0.36) | 0.81 | 0.77 | 0.74 | 0.61 | 0.81 | 0.75 | 0.63 | 0.77 | 0.66 | |
| 9 | (0.70, 0.51) | 0.70 | 0.68 | 0.71 | 0.57 | 0.70 | 0.71 | 0.57 | 0.72 | 0.56 | |
| 10 | (0.73, 0.50) | 0.91 | 0.91 | 0.89 | 0.89 | 0.90 | 0.89 | 0.79 | 0.88 | 0.81 | |
| 11 | (0.70, 0.51) | 0.80 | 0.81 | 0.85 | 0.72 | 0.81 | 0.85 | 0.73 | 0.84 | 0.75 | |
| Difference of the number of patients between A and B denoted by nA−nB | |||||||||||
| 7 | (0.70, 0.50) | −0.2 | 18.0 | 46.0 | 46.0 | 8.2 | 37.5 | 41.7 | 4.7 | 5.6 | |
| 8 | (0.56, 0.36) | −0.2 | 24.0 | 47.0 | 54.0 | 9.2 | 34.8 | 39.7 | 0.1 | −1.0 | |
| 9 | (0.70, 0.51) | 0.1 | 16.9 | 45.8 | 50.4 | 7.0 | 38.6 | 40.1 | 7.3 | 7.5 | |
| 10 | (0.73, 0.50) | −0.1 | 17.8 | 46.4 | 46.4 | 7.6 | 40.1 | 44.9 | 6.5 | 7.7 | |
| 11 | (0.70, 0.51) | 0.1 | 17.7 | 49.6 | 54.6 | 6.8 | 42.3 | 46.9 | 8.8 | 10.8 | |
| Number of failures | |||||||||||
| 7 | (0.70, 0.50) | 73.0 | 71.2 | 69.3 | 69.3 | 72.5 | 71.2 | 74.1 | 74.1 | 78.2 | |
| 8 | (0.56, 0.36) | 96.2 | 95.3 | 97.6 | 101.2 | 96.2 | 98.0 | 102.4 | 100.1 | 105.0 | |
| 9 | (0.70, 0.51) | 77.5 | 76.4 | 74.4 | 78.0 | 76.6 | 75.6 | 79.0 | 78.1 | 81.3 | |
| 10 | (0.73, 0.50) | 64.6 | 63.1 | 60.3 | 60.3 | 63.9 | 63.0 | 66.8 | 66.7 | 71.1 | |
| 11 | (0.70, 0.51) | 72.8 | 70.9 | 67.7 | 71.2 | 71.9 | 68.4 | 72.7 | 71.6 | 76.3 | |
RAR, response-adaptive randomization; CARA, covariate-adjusted RAR.
Table 8
| Sc. | (PA,PB) | Trad | RAR | CARA1 | CARA2 | CARA3 | CARA4 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| No adj | Adj | No adj | Adj | No adj | Adj | ||||||
| Estimated rejection probability (i.e., overall type I error rate) | |||||||||||
| 12 | (0.50, 0.50) | 0.05 | 0.05 | 0.06 | 0.06 | 0.06 | 0.08 | 0.02 | 0.09 | 0.03 | |
| 13 | (0.30, 0.30) | 0.04 | 0.05 | 0.09 | 0.00 | 0.05 | 0.01 | 0.02 | 0.11 | 0.00 | |
| 14 | (0.46, 0.46) | 0.05 | 0.05 | 0.09 | 0.02 | 0.03 | 0.09 | 0.02 | 0.09 | 0.02 | |
| 15 | (0.66, 0.66) | 0.05 | 0.05 | 0.09 | 0.02 | 0.04 | 0.09 | 0.03 | 0.10 | 0.02 | |
| Estimated rejection probability (i.e., power) | |||||||||||
| 16 | (0.69, 0.50) | 0.80 | 0.80 | 0.76 | 0.76 | 0.78 | 0.73 | 0.42 | 0.76 | 0.43 | |
| 17 | (0.63, 0.46) | 0.71 | 0.70 | 0.72 | 0.40 | 0.71 | 0.69 | 0.39 | 0.72 | 0.38 | |
| 18 | (0.72, 0.46) | 0.97 | 0.97 | 0.97 | 0.86 | 0.97 | 0.95 | 0.80 | 0.95 | 0.81 | |
| 19 | (0.41, 0.16) | 0.99 | 0.98 | 0.97 | 0.81 | 0.96 | 0.90 | 0.62 | 0.94 | 0.77 | |
| 20 | (0.58, 0.16) | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 | 1.00 | 1.00 | |
| Difference of the number of patients between A and B denoted by nA−nB | |||||||||||
| 16 | (0.69, 0.50) | −0.2 | 17.8 | 47.8 | 47.8 | 8.2 | 39.9 | 46.0 | 5.2 | 4.9 | |
| 17 | (0.63, 0.46) | −0.0 | 20.1 | 47.5 | 57.7 | 8.3 | 36.2 | 41.8 | 2.5 | 2.2 | |
| 18 | (0.72, 0.46) | −0.2 | 16.7 | 53.2 | 68.6 | 7.9 | 43.0 | 55.5 | 5.7 | 6.8 | |
| 19 | (0.41, 0.16) | 0.6 | 57.7 | 54.6 | 66.9 | 12.3 | 42.9 | 50.2 | −10.4 | −12.2 | |
| 20 | (0.58, 0.16) | 0.0 | 16.6 | 47.2 | 59.7 | 11.0 | 42.9 | 52.2 | −7.5 | 9.0 | |
| Number of failures | |||||||||||
| 16 | (0.69, 0.50) | 72.8 | 71.0 | 69.3 | 69.3 | 72.5 | 73.2 | 78.5 | 76.4 | 83.0 | |
| 17 | (0.63, 0.46) | 84.8 | 83.2 | 81.9 | 87.6 | 98.9 | 99.8 | 106.9 | 102.9 | 110.0 | |
| 18 | (0.72, 0.46) | 63.1 | 60.9 | 57.8 | 64.6 | 76.7 | 77.9 | 87.7 | 82.7 | 95.2 | |
| 19 | (0.41, 0.16) | 105.6 | 103.1 | 112.3 | 124.4 | 122.3 | 141.4 | 152.8 | 139.6 | 157.9 | |
| 20 | (0.58, 0.16) | 65.7 | 62.2 | 72.2 | 79.8 | 87.8 | 98.2 | 107.9 | 105.9 | 115.5 | |
RAR, response-adaptive randomization; CARA, covariate-adjusted RAR.
Our investigation using simulations took a general methodological approach in group sequential trials (i.e., for time points to analyze the data, trial duration, and so on). We assumed that prognostic/predictive biomarkers are available to see their effects and investigate the impact on the operating characteristics of the group sequential designs. We also considered two independent binary biomarkers with the main effect and the interaction effect with the treatment group, but more complicated situations (e.g., categorical or continuous biomarkers, correlated biomarkers, or high dimensional biomarkers) can be considered. Of note, the signal of the prognostic biomarkers has an impact on the overall type I error rate, and biomarkers with a strong signal due to the complicated situations will make the type I error rate inflation worse. Moreover, deviations of the planned setting due to medical or environmental changes as well as different situations from our setting are allowed and are worth investigating the impact of the biomarker-driven randomization.
In biomarker-driven trials, we assumed that investigators should have gone through a preliminary exploratory phase, including sufficient pre-clinical and clinical studies, to obtain a practical number of candidate biomarkers. It is not difficult from the statistical methodology perspective to add a burn-in stage performing variable selection, but it could make logistical difficulties in practice.
Conclusions
In this paper, we contributed to bringing the challenges and opportunities in biomarker-driven trials, especially for adaptive randomization incorporating biomarkers in group sequential trials. We found the type I error rate inflation and provided suggestions and considerations to preserve the type I error rate. However, following the suggestions, we observed a trade-off between controlling type I error rate and attaining clinical benefit (e.g., the difference of the number of patients allocated to two treatments and number of failures). Our strategies can help to maintain the type I error rate at the nominal level but could unnecessarily lose both power and clinical benefits, which implies the advantages of the biomarker-driven randomization are eliminated. It is critical to develop the statistical methods and designs which address unmet needs (i.e., clinical trial designs preserve the overall type I error rate while they keep ethics and improve clinical benefit compared to traditional fixed randomization and RAR) in biomarker-driven trials using biomarker-driven randomization.
Acknowledgments
Funding: This work was supported in part by University of Wisconsin-Madison Office of the Vice Chancellor for Research and Graduate Education.
Footnote
Provenance and Peer Review: This article was commissioned by the Guest Editors (Yanhong Deng, Qian Shi and Jun (Vivien) Yin) for the series “Challenges in Clinical Trials” published in Annals of Translational Medicine. The article has undergone external peer review.
Peer Review File: Available at https://atm.amegroups.com/article/view/10.21037/atm-21-6027/prf
Conflicts of Interest: The author has completed the ICMJE uniform disclosure form (available at https://atm.amegroups.com/article/view/10.21037/atm-21-6027/coif). The series “Challenges in Clinical Trials” was commissioned by the editorial office without any funding or sponsorship. The author reports that this work was supported in part by University of Wisconsin-Madison Office of the Vice Chancellor for Research and Graduate Education. The author has no other conflicts of interest to declare.
Ethical Statement: The author is accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Bailey AM, Mao Y, Zeng J, et al. Implementation of biomarker-driven cancer therapy: existing tools and remaining gaps. Discov Med 2014;17:101-14. [PubMed]
- De Maria Marchiano R, Di Sante G, Piro G, et al. Translational Research in the Era of Precision Medicine: Where We Are and Where We Will Go. J Pers Med 2021;11:216. [Crossref] [PubMed]
- Simon R. Review of Statistical Methods for Biomarker-Driven Clinical Trials. JCO Precis Oncol 2019;3:1-9. [Crossref] [PubMed]
- Freidlin B, Simon R. Adaptive signature design: an adaptive clinical trial design for generating and prospectively testing a gene expression signature for sensitive patients. Clin Cancer Res 2005;11:7872-8. [Crossref] [PubMed]
- Freidlin B, Jiang W, Simon R. The cross-validated adaptive signature design. Clin Cancer Res 2010;16:691-8. [Crossref] [PubMed]
- Zhang Z, Li M, Lin M, et al. Subgroup selection in adaptive signature designs of confirmatory clinical trials. J R Stat Soc Ser C Appl Stat 2017;66:345-61. [Crossref]
- Pan Y, Zhao YQ. Improved doubly robust estimation in learning optimal individualized treatment rules. J Am Stat Assoc 2021;116:283-94. [Crossref] [PubMed]
- Qiu H, Carone M, Sadikova E, et al. Optimal individualized decision rules using instrumental variable methods. J Am Stat Assoc 2021;116:174-91. [Crossref] [PubMed]
- Guo W, Zhou XH, Ma S. Estimation of Optimal Individualized Treatment Rules Using a Covariate-Specific Treatment Effect Curve With High-Dimensional Covariates. Journal of the American Statistical Association 2021;116:309-21. [Crossref]
- Simon N, Simon R. Adaptive enrichment designs for clinical trials. Biostatistics 2013;14:613-25. [Crossref] [PubMed]
- Magnusson BP, Turnbull BW. Group sequential enrichment design incorporating subgroup selection. Stat Med 2013;32:2695-714. [Crossref] [PubMed]
- Rosenblum M, Luber B, Thompson RE, et al. Group sequential designs with prospectively planned rules for subpopulation enrichment. Stat Med 2016;35:3776-91. [Crossref] [PubMed]
- Park Y, Liu S, Thall PF, et al. Bayesian group sequential enrichment designs based on adaptive regression of response and survival time on baseline biomarkers. Biometrics 2022;78:60-71. [Crossref] [PubMed]
- Thall PF. Adaptive Enrichment Designs in Clinical Trials. Annual Review of Statistics and its Application 2021;8:393-411. [Crossref]
- Nguyen Duc A, Heinzmann D, Berge C, et al. A pragmatic adaptive enrichment design for selecting the right target population for cancer immunotherapies. Pharm Stat 2021;20:202-11. [Crossref] [PubMed]
- Joshi N, Nguyen C, Ivanova A. Multi-stage adaptive enrichment trial design with subgroup estimation. J Biopharm Stat 2020;30:1038-49. [Crossref] [PubMed]
- Berry DA. The Brave New World of clinical cancer research: Adaptive biomarker-driven trials integrating clinical practice with clinical research. Mol Oncol 2015;9:951-9. [Crossref] [PubMed]
- Cecchini M, Rubin EH, Blumenthal GM, et al. Challenges with Novel Clinical Trial Designs: Master Protocols. Clin Cancer Res 2019;25:2049-57. [Crossref] [PubMed]
- Park Y. Review of Phase II Basket Trials for Precision Medicine. Annals of Biostatistics and Biometric Applications 2019;2.
- Yin G, Yang Z, Odani M, et al. Bayesian hierarchical modeling and biomarker cutoff identification in basket trials. Statistics in Biopharmaceutical Research 2021;13:248-58. [Crossref]
- Psioda MA, Xu J, Jiang Q, et al. Bayesian adaptive basket trial design using model averaging. Biostatistics 2021;22:19-34. [Crossref] [PubMed]
- Ouma LO, Grayling MJ, Zheng H, et al. Treatment allocation strategies for umbrella trials in the presence of multiple biomarkers: A comparison of methods. Pharm Stat 2021;20:990-1001. [Crossref] [PubMed]
- Rosenberger WF, Vidyashankar AN, Agarwal DK. Covariate-adjusted response-adaptive designs for binary response. J Biopharm Stat 2001;11:227-36. [Crossref] [PubMed]
- Thall PF, Wathen JK. Covariate‐adjusted adaptive randomization in a sarcoma trial with multi‐stage treatments. Statistics in Medicine 2005;24:1947-64. [Crossref] [PubMed]
- Hu J, Zhu H, Hu F. A Unified Family of Covariate-Adjusted Response-Adaptive Designs Based on Efficiency and Ethics. J Am Stat Assoc 2015;110:357-67. [Crossref] [PubMed]
- Villar SS, Rosenberger WF. Covariate-adjusted response-adaptive randomization for multi-arm clinical trials using a modified forward looking Gittins index rule. Biometrics 2018;74:49-57. [Crossref] [PubMed]
- Zhao W, Ma W, Wang F, et al. Incorporating covariates information in adaptive clinical trials for precision medicine. Pharm Stat 2022;21:176-95. [Crossref] [PubMed]
- Jackson H, Bowen S, Jaki T. Using biomarkers to allocate patients in a response-adaptive clinical trial. Commun Stat Simul Comput 2021;1-20. [Crossref]
- Boruch RF. Randomized controlled experiments for evaluation and planning. Handbook of applied social research methods Thousand Oaks, CA: Sage Publications 1998:161-92.
- Bickman L, Reich SM. Randomized controlled trials: A gold standard with feet of clay. What counts as credible evidence in applied research and evaluation practice 2009:51-77.
- Neyman J. On the two different aspects of the representative method: the method of stratified sampling and the method of purposive selection. Breakthroughs in statistics. Springer; 1992. p. 123-50.
- Rosenberger WF, Stallard N, Ivanova A, et al. Optimal adaptive designs for binary response trials. Biometrics 2001;57:909-13. [Crossref] [PubMed]
- Thall PF, Wathen JK. Practical Bayesian adaptive randomisation in clinical trials. Eur J Cancer 2007;43:859-66. [Crossref] [PubMed]
- Yin G, Chen N, Lee JJ. Phase II trial design with Bayesian adaptive randomization and predictive probability. J R Stat Soc Ser C Appl Stat 2012;61:219-35. [Crossref] [PubMed]
- Wei L, Durham S. The randomized play-the-winner rule in medical trials. Journal of the American Statistical Association 1978;73:840-3. [Crossref]
- Muliere P, Paganoni AM, Secchi P. A randomly reinforced urn. Journal of Statistical Planning and Inference 2006;136:1853-74. [Crossref]
- Hu F, Zhang L-X. Asymptotic properties of doubly adaptive biased coin designs for multitreatment clinical trials. The Annals of Statistics 2004;32:268-301. [Crossref]
- Duan L, Hu F. Doubly adaptive biased coin designs with heterogeneous responses. Journal of Statistical Planning and Inference 2009;139:3220-30. [Crossref]
- Proschan M, Evans S. Resist the Temptation of Response-Adaptive Randomization. Clin Infect Dis 2020;71:3002-4. [Crossref] [PubMed]
- Karrison TG, Huo D, Chappell R. A group sequential, response-adaptive design for randomized clinical trials. Control Clin Trials 2003;24:506-22. [Crossref] [PubMed]
- Thall P, Fox P, Wathen J. Statistical controversies in clinical research: scientific and ethical problems with adaptive randomization in comparative clinical trials. Ann Oncol 2015;26:1621-8. [Crossref] [PubMed]
- Mathew OO, Sola AF, Oladiran BH, et al. Efficiency of Neyman allocation procedure over other allocation procedures in stratified random sampling. American Journal of Theoretical and Applied Statistics 2013;2:122-7. [Crossref]
- Hart RG, Halperin JL, Pearce LA, et al. Lessons from the Stroke Prevention in Atrial Fibrillation trials. Ann Intern Med 2003;138:831-8. [Crossref] [PubMed]
- O'Brien PC, Fleming TR. A multiple testing procedure for clinical trials. Biometrics 1979;35:549-56. [Crossref] [PubMed]
- FDA. Adaptive designs for clinical trials of drugs and biologics. 2019.